灰色关联在城市轨道交通线网规划方案评价中的应用

任 乐

(上海海事大学交通运输学院,200135,上海∥博士,讲师)

城市轨道交通线网规划受自然、社会、经济、环境和工程技术等各项因素的影响和制约,因此方案的形成具有多样化倾向;同时,规划目标要求的多样性又使轨道线网规划成为一个确定性、准确性与随机性、模糊性的目标统一体。由于系统规模的大型化及内涵的复杂化,规划方案设计过程中涉及的因素错综复杂,故在方案论证阶段,对备选方案的评价与选择极其重要。

结合城市轨道交通线网规划方案评价的特点,使用层次分析(AHP)与灰色关联系数法结合的AHP-Gray方法进行线网方案评价。AHP法能把复杂问题分解为若干因素,区分评价对象指标的层次性,确定各因素对总目标的相对重要性权重,具有高度逻辑性、灵活性及简洁性的特点[1]。灰色关联系数法是灰色系统理论[2-3]的重要组成部分,其基本思想是根据序列曲线几何形状的相似程度来判断灰色过程发展态势的关联程度,用来处理信息不完全确知的系统。它能充分利用系统已有的白化信息,并着重从系统内部行为数据间的内在联系上挖掘信息及其量化的方法。

1 城市轨道交通线网方案评价指标各因素权重的确定

1.1 评价指标体系构成

遵循全面性、可操作性、目的性、非相容性和客观公正性的原则[4]建立三个层次、四个子系统的城市轨道交通线网方案评价AHP指标体系如图1。

1.2 层次分析法确定指标权重

若求最下层各指标相对于最上层总目标的权重是比较困难的,但是如果分层求出本层各指标对于上层指标的相对重要性(分层权重),最后求出最下层指标对于总目标的权重则比较容易。运用AHP法计算权重时通常有权的最小平方法、幂法、和法、方根法等。权重计算的程序如图2所示。

1.2.1 判断矩阵A={aij}建立及求解

判断矩阵可由专家和决策者给出。AHP创始人T.L.Satty提出的1～9标度法建立判断矩阵,能较准确地将思维判断数量化,且繁简适中。设某层次共有n个指标与上一层次的某指标相联系。第i个指标对第j个指标的相对估计值记作aij,并近似地认为是指标i的权w i和指标j的权w j之比。n个指标成对比较的结果用矩阵A表示。若A阵估计正确,下式应严格相等,齐次方程组(I为单位阵)对于未知向量W只有平凡解;否则,A阵元素小的扰动意味着特征值小的摄动,从而AW=λmax W。W的分量即为所要求的指标对上一层指标的权重。由于 A具有特殊结构,可采用一些近似计算方法,如方根法、和法等,这在A具有较好的一致性情况下不会产生很大误差。

图1 城市轨道交通线网规划综合评价指标体系

图2 AHP权重计算程序

1.2.2 判断矩阵一致性检验

由于决策问题的复杂性及各指标间相对重要程度的模糊性,有时候式aij=aik akj不能得到完全的满足。根据矩阵理论,引入一致性指μ=0(即λmax=n)时,判断矩阵具有完全一致性。若μ≠0,则 μ越大,判断矩阵偏离完全一致性越远。同时,对于多阶判断阵,引入判断矩阵的平均随机一致性指标 R(见表1)。考查 μ的随机性,确定一个临界值 μ0,对于矩阵 A,当一致性指标 μ满足 μ≤μ0=0.1×R时,认为 A有满意的一致性。

表1 平均随机一致性指标R值

1.2.3 指标总权值的计算

由程序计算指标总权值的结果如表2。

表2 指标权重表

2 城市轨道交通线网规划方案灰色关联评价模型

2.1 决策矩阵的建立

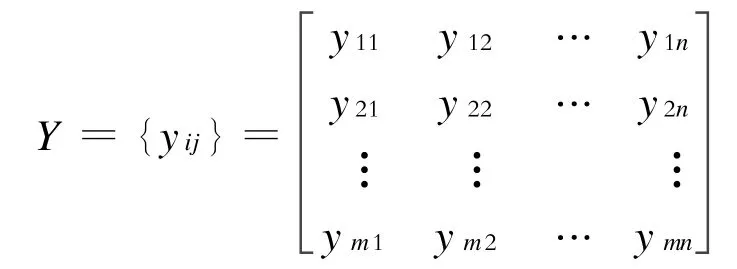
它提供了分析决策问题的基本信息。

指标中既有定性指标又有定量指标。定量指标可从有关部门提供的资料中获得。对于定性指标,首先根据集值统计评分轴对各方案定性指标进行详细描述分析,在此基础上采用Delphi法评分按集值统计的方法确定定性指标的值。

2.2 最优指标集的确定及决策矩阵规范化

要对各个方案进行综合评价,首先必须制定评价标准。制定评价标准时,既要考虑到标准的先进性,又要考虑到标准的可行性。选择各方案各指标中的最优值作为最优指标集,作为比较的基准。按各项指标的最优值,可列出最优指标集

各指标的单位不同,数值上也有很大的差别,指标之间具有不可公度性,难于直接比较。因此,必须把各指标的值都统一变换到某一个度量范围内,形成规范化的决策矩阵E={eij},消去量纲。本文采用极差规范化的方法对决策矩阵进行规范化。该方法优点是基点相同,变换后0≤eij≤1。规范化后的

效益型指标

2.3 计算灰色关联系数

将经规范化后的最优指标集{e*}=[e*1,e*2,…,]作为参考数据列,经规范化后各方案的各指标集}=[,…,]作为被比较数列。其中i=1,2,…,m;k=1,2,…,n。则可按下式分别计算第i方案第j个决策指标与第j个最优指标的关联系数g i(j)。式中ρ为分辨率,ρ∈[0,1],一般取ρ=0.5。

2.4 综合评价及方案排序

线网方案评价选优灰色方法的数学模型为:

若关联度ri最大,则说明{eij}与最优指标集最接近,也就是说i方案优于其它方案,并可据此排出各方案的优劣顺序。

3 案例研究

本文以重庆市快速轨道交通线网规划方案的评价为例。表3为重庆市轨道交通线网规划的备选方案简况。

表3 重庆市轨道交通线网规划备选方案基本情况[5]

现采用AHP-Grey法评价各方案的优劣顺序。其步骤如下:

①建立评价指标体系(如图1所示)。

②确定评价指标体系中各因素的权重(见表2)。

③按2.1节所述方法,分析和计算得到决策矩阵如表4所示。

表4 决策矩阵Y

④按2.2节所述方法,确定最优指标集H*,构造扩大的决策矩阵Y进而采用极差规格化方法得到规范化决策矩阵E。

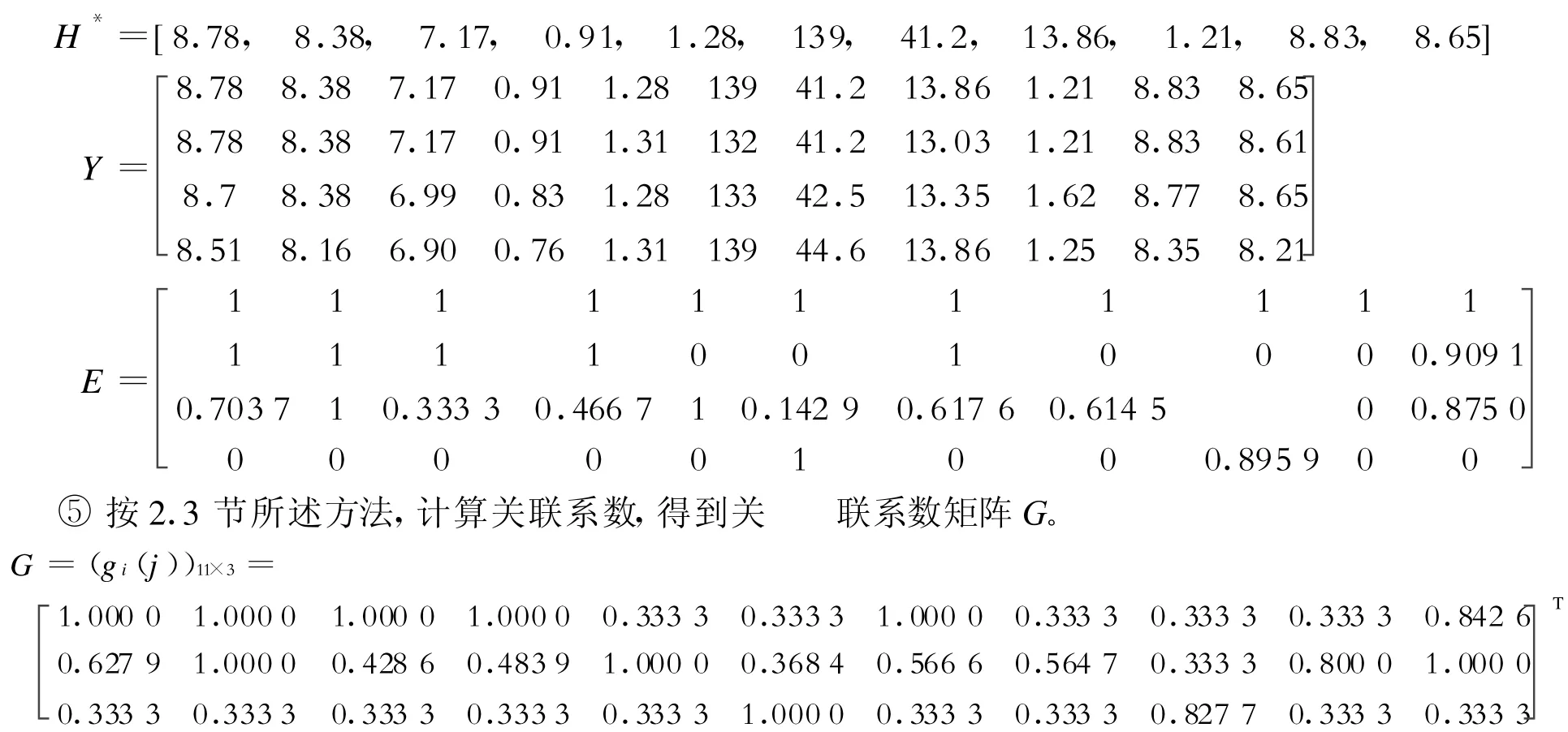
⑥进行综合评价及方案排序。按灰色关联的分析原则,灰色关联度ri越大,说明方案越好。按2.4节所述方法计算ri,得到各方案排序如下:方案1(0.730 2)＞方案 2(0.640 2)＞方案3(0.395 2)。由此可见,方案1最优,方案3最劣。

4 结语

灰色关联分析法能够充分利用实际方案中的指标值构造最优指标集,利用灰色关联度作为测度进行综合评价,确定各方案指标与相对方案指标的类似程度。AHP-Grey法既充分体现了各指标对总目标的重要性程度,又充分利用并挖掘了决策矩阵中的有效信息,是一种简便而适用的方法。如果能用更为客观、科学的方法确定指标的重要性权重,则城市轨道交通线网规划方案的评价工作将会更为科学合理。

[1]吴小萍.可持续发展战略指导下的轨道交通规划与评价方法研究[J].中国工程科学,2004,25(1):140.

[2]刘思峰,郭天榜,党建国,等.灰色系统理论及其应用[M].北京:科学出版社,1998.

[3]姜旭平.经营分析方法与IT工具[M].北京:清华大学出版社,2002.

[4]杨东援.交通规划决策支持系统[M].上海:同济大学出版社,1997.

[5]周涛.重庆市主城区轨道交通线网规划[R].重庆:重庆市规划局,2003.