基于灰色关联度分析的模拟电路故障诊断

秦福星 周庆年 吕飞 张松涛

（海军蚌埠士官学校，安徽蚌埠 233012）

1 引言

灰色系统理论是由我国的邓聚龙教授于1982年创建的。灰色系统理论认为，客观世界是信息的世界，把已知的确定的信息称为白色信息，未知的不确定的信息称为黑色信息，既含有未知信息又含有已知信息的系统称为灰色系统。灰色系统理论着重研究“部分信息明确，部分信息不知”的贫信息的不确定性系统，在工业、农业、经济和军事等领域都得到了广泛的应用。灰色系统理论包括灰色预测、灰色关联度分析、灰色聚类和灰色决策等内容[1-3]。灰色关联度分析的基本任务是基于行为因子序列的几何接近，以分析和确定因子间的影响程度或者因子对主行为的测度关系[4]。灰色关联度分析是灰色系统分析和处理随机量的一种方法，代表了不同研究对象(灰色因数)之间的关联程度，是一种数据到数据的“映射”。一般情况下，电路中存在着元件容差，使得电路的测量数据存在着模糊和不确定的信息，电路故障与故障征兆之间并不是一一对应的关系，没有确定的映射关系，因此可将模拟电路看作是一个复杂的灰色系统。而灰色关联度分析在处理此种不确定信息方面有着独到的优势，因此，非常适合于容差模拟电路的故障诊断。

2 诊断原理

2.1 灰色关联度诊断算法[5-7]

评价系统因子之间关联程度的指标称为灰色关联度。令x0表示参考序列，xi表示比较序列，其中，k=1，2，…，m；i =1，2，…，n。那么，参考序列与比较序列之间在k点的关联系数ξ(k)可由式（1）得出。

在（1）式中，ρ为分辨系数， 0＜ρ＜1，一般情况下取0.5。

这样一来，参考序列x0和比较序列xi之间的关联度可由式（2）得出。

由此可见，利用灰色关联度分析对容差模拟电路进行故障诊断时，需要确定参考序列和比较序列。在电路故障诊断时，一般情况下可以将电路的实测数据作为参考序列，而将电路的故障仿真数据看作比较序列。比较序列可以看作诊断的标准，因此，获取足够多和足够精确的仿真数据是测量的关键之一。因此必须正确地选定电路的测试点。测试点的选择一般需要遵循以下两条原则[1]：

(1)可测试点尽可能多。测试点越多，对电路的描述就越清楚，获取的信息量就越大，诊断结果就越准确。

(2)合理选择可测试点，使其能够尽可能多的暴露电路故障模式。

上述两大原则只是在一般意义上成立，尤其对第一条来说，测试点越多，意味着测试工作量就越大。因此，在确定测试点数量时，必须同时考虑工作量和电路描述的精度，在保证满足电路描述精度的前提下，尽可能的降低工作量。

2.2 诊断步骤

（1）选择模拟电路若干个电路状态模式向量。

（2）通过对电路正常状态样本的仿真计算，建立标准正常状态模式向量；通过对电路各种故障状态下样本的仿真计算，建立标准故障状态模式向量。最终得到电路标准状态模式向量——标准状态矩阵x0，作为参考矩阵。

（3）通过对实际故障电路进行电压测量计算，确定故障电路的状态模式向量——实际故障状态模式矩阵xi，作为比较矩阵。

（4）利用式（1）分别计算故障状态模式向量和标准状态模式向量之间的关联度系数。关联度系数为ζ(k)，ζ(k)表示待测状态模式向量xi对标准状态模式向量x0在k点的关联度系数。ζ(k)在[0，1]之间取值，ζ(k)越大，表示两种模式向量更接近。

（5）由于关联系数的数值很多，信息过于分散，不便于比较，因此利用式（2）计算关联度，作为诊断系统所处的状态的参数Yi。Yi表示xi和x0的关联程度。Yi越大说明关联程度越高。

（6）根据关联度大小判断故障电路故障状态的实际情况。计算电路故障状态模式与标准状态模式向量之间的关联程度，按关联度的大小判断待测模式与哪个标准状态模式更接近，则电路故障模式与那个标准状态模式更接近，从而实现模拟电路故障状态的识别。

3 诊断实例

诊断实例：取典型的模拟电路——两级放大电路为例进行诊断，说明基于灰色关联度分析法在容差模拟电路中的故障诊断应用。电路如图 1所示，可测试节点为1，2，3，4。限于篇幅，这里只给电路设定3种故障状态，虽然故障状态较少，但并不影响诊断方法的演示，其他复杂电路和更多的故障状态可以类似进行诊断。对电路正常状态和故障状态进行 PSPICE电路仿真后，得到如表1所示的测试节点电压情况：

表1 测试节点仿真电压值

图1 两级放大电路

获得仿真数据之后，针对实际电路，使VT1 be短路，测可测试节点的实际电压，所得到的实际数据如表2所示：

表2 实测电压数据

对比表1和表2可以发现，由于模拟电路中容差的存在，使故障仿真数据和实际测量数据之间存在一定的差别。

以VT1 be短路的实测数据作为比较序列y0，表1中的数据作为参考序列yi，(i=1，2，3，4)。将上述比较序列和参考序列进行归一化得到。

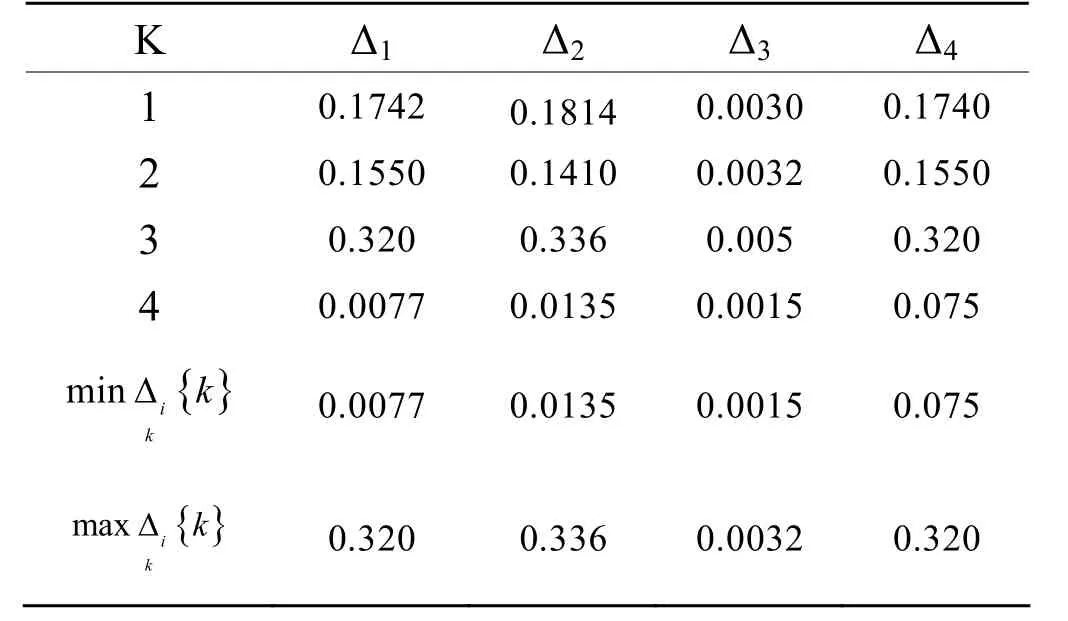
表3 计算结果

令ρ=0.5，根据式（1）求得关联系数分别为：

根据式（2）可以得到4个不同的关联度，即实测结果 VT1 be短路与仿真数据之间的关联程度，关联度越大，说明该数据属于 VT1 be短路这一故障的可能性就越大。得到的4个关联度如表4所示：

表4 关联度值

可以看出，关联度Y3值最大，而且比其它关联度要大得多。因此，可以认为，此时的故障为VT1 be短路。这与实际故障情况是一致的。

3 结论

通过本文分析实例可以看出，灰色关联度诊断法进行模拟电路的故障诊断，具有计算简单，结论客观全面等特点。通过正确选定电路测试点，在保证一定工作量前提下，获取足够多和精确的仿真数据，建立合理的标准故障状态模式，就可以获得较高的诊断精度，成功解决模拟电路的故障诊断与容差问题。

理论上，我们可以仿真计算出模拟电路在主要故障模式下的可测试电路节点的电压值，也就能得到完备的标准故障状态的模式向量，即完备参考序列x0。在电路发生实际故障时，我们对故障电路的相同可测试电路节点进行电压的测量，得到实际故障下的节点电压值即比较序列 xi，通过计算比较序列xi与参考序列x0的关联度，按关联度的大小判断待测模式与哪个标准状态模式更接近，便可进行电路故障的识别。这样就能较好地解决电路中元件的容差问题。

[1]贺晓, 刘景宁, 李淑霞等. 基于灰色关联理论的案例推理在故障智能诊断系统中的应用[J]. 中国机械工程, 2004, 15(22)：2022-2026.

[2]邓聚龙. 灰色系统基本方法[M]. 武汉： 华中理工大学出版社, 1987.

[3]吴宜亮, 李小民, 冯永利等. 灰色关联度分析法在级差式空压机故障诊断中的应用[J]. 微计算机信息,2006, 2 （25）：81-84.

[4]Liu Gousheng，Yu Jianguo.Gray Correlation Analy-sis and Prediction Models of Living Refuse Genera-tion in Shanghai City[J].Waste Management, 2006： 19：1-7

[5]Zhu Chihui，Li NianPing，Re Di，et al. Uncertainty in Indoor Air Quality and Grey System Method[J].Building and Environment, 2007, 42(4)：1711-1717.

[6]Chian Ko Tag, Chang Fu Ping, Tsai Te Chang.Opti-mum Design Parameters of Pin - fin Heat Sink Using the Grey-fuzzy Logic Based on the Orthogo-nal Arrays[J]. International Communications inHeat and Mass Transfer, 2006, 33：744-752.

[7]Chan J W K, Tong T K L. Multi- criteria Material Selections and End-of-life Product Strategy： Grey Relational Analysis Approach [J]. Materials and Desing, 2007, 28(5)：1539-1546.