CALCULATION OF ADDED MASS OF A VEHICLE RUNNING WITH CAVITY*
2010-07-02LIJie
LI Jie
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China,
E-mail: lijie@sjtu.edu.cn
LU Chuan-jing
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China
State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China
HUANG Xuan
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China
CALCULATION OF ADDED MASS OF A VEHICLE RUNNING WITH CAVITY*
LI Jie
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China,
E-mail: lijie@sjtu.edu.cn
LU Chuan-jing
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China
State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200030, China
HUANG Xuan
Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai 200240, China
A numerical method is developed to obtain the added mass coefficients of a vehicle running with cavity in numerical simulation for the multiphase flow of the vehicle which is imposed an added vibration and analyzing its hydrodynamic loads. The method is verified through the cases of non-cavitating sphere and ellipsoid. The changing rule of the added mass of a sphere during water exit is gained. Then the influence of cavitation on the added mass of a cylinder is studied. The results show that λ11, λ22, λ26, λ66all decrease as the cavitation number reduces and the length of the attached cavity increases. There is almost a linear relationship between the cavity length and λ22.The base cavity has great influence on λ11, its contribution decreases more than 60%, when the cavitation number changes from 0.6 to 0.2.
added mass, cavity carrying, forced vibration method
1. Introduction
Whenever a body is in accelerated motion relative to surrounding fluid, it will be imposed an additional inertial force, which could be attributed to an equivalent added mass of fluid. The added mass is a classical concept and has been widely studied for many years. The added mass effect was discovered by Du Buat in 1786 and Friedrich Bessel in 1828 independently. The added mass is of fundamental importance in hydrodynamic research.
The added mass was studied numerically for several decades. Most numerical works for the issue were done on the basis of the potential theory. Both the BEM and FEM can be applied to determine the added mass for an object of complex shape moving in an unbound region[1,2]. For example, Lin[3]and Liu[4]studied the added mass of submarine and airship by solving the potential flow problem with the Hess-Smith method. Many experimental techniques were also developed to investigate the added mass, such as free oscillation[5], forced oscillation[6]inertia method, etc.. Thus the added mass are all extracted from the hydrodynamic characters for vibration. A novel parameter identification method based on a TSK fuzzy system was reported by Chen et al.[7], which canbe effectively used to determine the added mass changing with time, i.e., for the case of water exit. With the advancement in CFD methods, numerical methods to calculate added mass were worked out by simulating accelerated flows directly[8-10].
For a cavity-carrying vehicle, the added mass depends not only on its shape, but also on other kinematic and dynamic parameters. Less work has been done for finding the added mass in this case. With the potential theory, Uhlman[11]studied the added mass of supercavitating body in surge. Zhu[12]investigated the added mass of a slender body running with cavity by experiment in a cavitation tunnel.
In this article, a new numerical method is developed to predict the added mass of cavitycarrying bodies. The method is verified by comparing the present numerical results with the analytical solutions of non-cavitating sphere and ellipsoid moving in unbounded fields. Then, the evolution of the added mass of non-cavitating sphere during water exit and the influence of cavitation on the added mass of the moving vehicle are studied.
2. Method of calculating added mass
The present method to predict the added mass of a body running with cavity is based on calculating hydrodynamic forces of the body which is imposed by an added vibration. It includes two main steps. First, the multiphase flow field of body running with cavity, which is forced to vibrate with small amplitude and high frequency according to scheduled rule, is simulated numerically and the evolution of hydrodynamic forces are calculated. Then, the added mass coefficients are extracted from the numerical data of hydrodynamic load with the Fourier analysis. The following two sections will explain the steps succesively.
2.1Numerical simulation of multiphase flow
The homogeneous equilibrium model[13]based on the isotropic RANS equations is adopted to simulate the multiphase flow. The mixture of vapor and water is thought as single fluid with changeable density. All phases share the fields for all variables and properties. The slip velocity between the phases is ignored. The following governing equations are given to describe the multiphase flow of vapor and water by introducing the volume fraction variableαfor each phase[14,15].
The continuity equation and RANS equation are

whereuiandxirepresent the velocity components and the coordinates,tis the time,pdenotes the local pressure, the densityρand the viscosityμof mixture are computed in a volume-fraction-average manner,μtdenotes the turbulent viscosity.
The continuity equation for the vapor phase is

The subscriptvrefers to vapor. The mass transfer processes in Eq.(3) is expressed as[16]

wheren0is defined as nuclei concentration per unit volume of liquid,pvis the equilibrium vapor pressure,ρlis density of liquid.
The mathematic model is made closed by using the two-equation RNGk−εmodel:


wherekis the turbulent kinetic energy andεis the dissipation rate. The turbulent viscosityμtis given as

The finite volume method is employed to discretize the integral-differential equations, and the SIMPLE scheme is adopted to solve the pressurevelocity coupling problem. The second-order upwind scheme is applied to discretize the momentum equations. The first-order upwind scheme is used for the turbulent transportation equations. The moving-grid technology is applied to adapt the changing flow domain.
The computational model and the boundary conditions for the problem is shown in Fig.1.

Fig.1 Computational model
2.2Method of extracting the added mass

For the forced vibration of a body in an incoming flow as shown in Fig.1, the velocity of body forced relative to fluid is: whereVis the velocity of incoming flow, andvis the forced vibration velocity of the body. It is assumedvis much smaller thanV. To obtain thecomponent of added massλij, let the body vibrate with the mode

where the subscripti=1,2,3 represent the translational mode,i=4,5,6 the rotational mode,Aithe amplitude of vibration velocity,ωthe vibration frequency.
The present method is also applicable to slowly varying motions so long as the vibration period is far shorter than the time scale of income flowV. For simplicity, here assumeVis a constant.
The hydrodynamic forceFimposed on the body is a function of the incoming velocityV, vibration velocityvandaccelerationv. With the Taylor series expansion to the first order, it can be expressed as

The terms on the right side of Eq.(10) are the force components corresponding to position, damping and inertia. From the definition of added mass, it follows that

Substituting Eqs.(9) and (11) into Eq.(10) yields:

With the Fourier analysis, the added mass can be written as
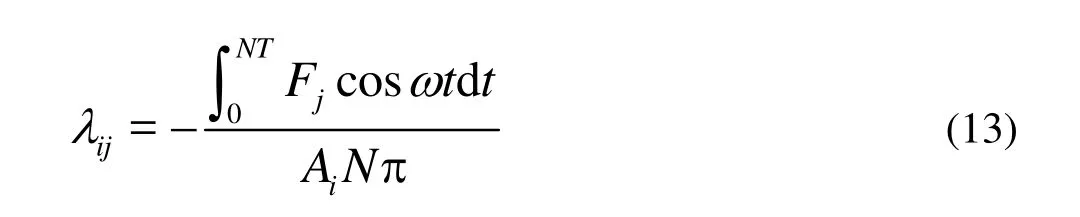
whereNis the number of vibration period,Fjis the hydrodynamic force in time domain, which is recorded by pressure integral over the body surface, easy to obtained during numerical simulations.
3. Verification of the method
The cases of non-cavitating sphere and ellipsoid moving in unbounded flow fields are taken as typical benchmarks to verify the present method. The effects of vibration frequency, vibration amplitude, time step and mesh dependence are examined through a series of numerical experiments.
3.1Added mass of sphere
The added mass of a full wetted rigid sphere vibrating in water is calculated first. Its radiusR=0.4m , the upstream velocityV=10m/s, and thevibration velocityv1=A1sinω1t, whereA1=0.1m/s,ω1=2π×100, and the period is 0.01 s. The drag coefficient obtained is shown in Fig.2, LetN=5, then the calculated value of the added mass is 134.49 kg according to Eq.(13). Compared to the analytical solution of potential flow 2/3ρπR3(=133.8kg ), the error is smaller than 1%. The error comes from numerical error and viscous effect. The latter is known as a positive factor to increase the added mass not more than 0.1 percent. For the present case, the viscous effect can be neglected.

Fig.2 Drag coefficient of sphere
Figure 3 shows the time evolution of added mass. It can be seen that the result is almost invariable along with the time.

Fig.3 Added mass of sphere vs.time
3.2Added mass of ellipsoid
For the added mass matrix of ellipsoid, there are three non-zero components:λ11,λ22andλ66. To gain these components, corresponding oscillatory movements, namely surge along the major axis, sway along the minor axis and pitch movement should be simulated respectively. In the calculated cases, the semimajor axisa=0.8m, and the semiminor axisb=0.4m. The upstream velocity and vibration velocity are the same as those for sphere. The numerical results are in good agreement with the analytical ones, and all the errors are smaller than 1% as shown in Table 1.

Table 1 Added mass of ellipsoid
4. The added mass of sphere during water exit
The added mass is proportional to the fluid density. So the added mass in water is much larger than in air. For an object exits from water, its added mass will keep reducing until it is out of water completely.
The vertical water exit of a sphere of radiusR=0.4m with the constant velocityV=10m/s is simulated numerically. The interface of water and air is caught by the VOF method. The vibration frequencyωis taken as 2π×500, which is high enough to ensure the vibration period (0.002 s) is far shorter than the time scale of water exit (2R/V=0.08s).
Figure 4 describes the calculated results of the added mass for the sphere. The data can be fit by using the following formula:

wherehis the vertical distance from the sphere top to still water surface, andλ0the added mass of sphere in unbounded flow field.
The change rate of added mass is

while ash/R=2,dλ/dtreaches its minimum

It means the added mass is of the maximum reducing rate at the position ofh/R=2.

Fig.4 Added mass during water exit
5. Added mass of a vehicle running with cavity
When an underwater vehicle moves with high speed, the cavities developed on its nose (attached cavity) and bottom (base cavity) will affect hydrodynamic forces directly. Therefore the added mass of the vehicle can be far different from that in fully wetted case. Although it can hardly be predicted by the classic potential flow theory, it is solved with the present method so long as the cavitating flow can be simulated correctly.
Here, a cylinder with the slender ratio greater than 10 is chosen. Its head part and tail part are both spherical crowns. The lengthL=1.0m and the radiusR=0.075m.The other geometrical parameters described in Fig.5 are:L1=0.06m ,L2=0.56m,L3=0.34m andL4=0.04m.

Fig.5 Shape of cylinder
The numerical results of cavity shape for several cavitation numbers are shown in Fig.6. The relationship between the cavity lengthLσand cavitation numberσis presented in Fig.7. The shape of cavity shows itself unstable characters in the unsteady calculation scheme especially for larger
cavitation number, and the cavity length is defined as the time-average value. The total forces gained are divided into three parts: the loads on the head, body and tail, so that the contribution of each part to the added mass can be analyzed.

Fig.6 Cavity shape for different values ofσ

Fig.7 Relationship between σ andLσ
The numerical results show that the added mass coefficientsλ11,λ22,λ26andλ66all decrease as cavitation number reduces and the cavity length increases (see Fig.8). For the axial componentλ11, the body part has no contribution, the head and tail parts have almost equal contribution in the fully wetted case (Lσ=0). The contributions toλ11by the head and tail reduce with the development of cavity. The value ofλ11due to the tail part will reduce by 60% as the cavitation number is 0.2, whileλ11due to the head reduce slowly.
For the present vehicle, the main contributions toλ22,λ26andλ66are from its body part. Both the head and tail part have small effects. On the whole,λ22,λ26andλ66reduce monotonously asLσincreases. There is almost linear relationship betweenλ22andLσ. Hereλ26andλ66are defined both relative to the center of mass, and they reduce quickly as the cavity grows.
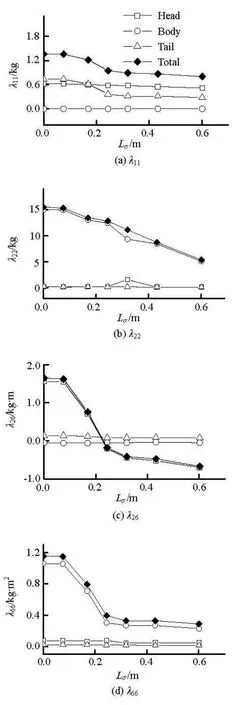
Fig.8 Rrelationship between added mass and cavity length
6. Conclusions
A numerical method for predicting the added mass of a body running with cavity has been developed in this article. The method includes two main steps. First, the multiphase flow of the body which is imposed to vibrate with small amplitude and high frequency is simulated to obtain the hydrodynamic forces. Then, the added mass coefficients are extracted through the Fourier analysis on the hydrodynamic force data. The method is verified with the cases of non-cavitating sphere and ellipsoid moving in unbounded flow fields.
The changing rule of the added mass of a sphere during water exit is gained. A formula is fit based on the numerical data. It means the added mass is of the maximum reducing rate at the positionh/R=2.
The influence of cavitation on the added mass of a cavity running vehicle is studied. the results show thatλ11,λ22,λ26andλ66all decrease as the cavitation number reduces and the cavitation length increases. The base cavity has great influence onλ11, and its contribution decreases by more than 60%, as the cavitation number decreases from 0.6 to 0.2. There is almost linear relationship between attached cavity lengthLσandλ22.
[1] LI Hua-dong, ZHU Xi and LUO Zhong et al. Boundary element method for solving added mass of structure[J].Journal of Naval University of Engineering,2009, 21(2): 45-49(in Chinese).
[2] LEUNG A. Y. T., FOK A. S. L. and Dai H. et al. The fractal finite element method for added-mass-type problems[J].International Journal for Numerical Methods in Engineering,2008, 75(10): 1194-1213.
[3] LIN Chao-you, ZHU Jun. Numerical computation of added mass of submarine maneuvering with small clearance to sea-bottom[J].Ship Engineering,2003, 5(1): 26-29(in Chinese).
[4] LIU Dan, WANG Xiao-liang and SHAN Xue-xiong. Added mass to stratospheric airship and its effect on motion[J].Computer Simulation,2006, 23(6): 52-56(in Chinese).
[5] KUWABARA Joji, SORNEYA Sotoshi. Experimental investigation of added mass coefficient with a free oscillating circular cylinder[J].Japan Society of Mechanical Engineering,2008, 74(6): 1396-1401.
[6] PAN Guang, WEI Gang and DU Xiao-xu. Whole scheme of added mass's forced oscillatory mechanism[J].Measurement and Control Technology,2007, 26(1): 35-37(in Chinese).
[7] CHEN Wei-qi, YAN Kai and SHI Gan-jun et al. Parameter identification of hydrodynamic forces of water-exit body based on TSK fuzzy system[J].Journal of Hydrodynamics Ser. A,2005, 20(4): 446-451(in Chinese).
[8] SHEN Ding-an, LIU Hong-mei. Maneuvering performance in the shallow water of large-scale ships[J].Journal of Ship Mechanics,2009, 13(5): 727-733(in Chinese).
[9] YANG Lu-chun, PANG Yong-jie and HUANG Li-hua et al. Study of the CFD approach to simulate PMM experiments of submarine[J].Ship Science and Technology,2009, 31(12): 12-17(in Chinese).
[10] ZHU Ren-chuan, GUO Hai-qiang and MIAO Guo-pinget al. A computational method for evaluation of added mass and damping of ship based on CFD theory[J].Journal of Shanghai Jiaotong University,2009, 43(2): 198-203(in Chinese).
[11] UHLMAN J. S., FINE N. E. and KRING D. C. Calculation of the added mass and damping forces on supercavitating bodies[C].Proceedings 4th International Symposium on Cavitation.Pasadena, CA, USA, 2001.
[12] ZHU Xiao-min, YAN Kai and JIANG Han-ming, Experimental investigation on added mass of slender bodies of revolution running with cavity[J].Journal of Ship Mechanics,1998, 2(5): 28-34(in Chinese).
[13] CHEN Ying, LU Chuan-jing. A Homogeneousequilibrium-model based numerical code for cavitation flows and evaluation by computation cases[J].Journal of Hydrodynamics,2008, 20(2): 186-194.
[14] CHEN Ying, LU Chuan-jing and WU Lei. Numerical method for three dimensional cavitation flows at small cavitation numbers[J].Journal of Computational Physics,2008, 25(2): 163-170(in Chinese).
[15] OKITA K., UGAJIN H. and MATSUMOTO Y. Numerical analysis of the influence of the tip clearance flows on the unsteady cavitating flows in a three-dimensional inducer[J].Journal of Hydrodynamics,2009 21(1): 34-40.
[16] YUAN Wei-xing, SCHNERR G. H. Cavitation in injection nozzles effect of injection pressure fluctuations[C].Proceedings 4th International symposium on Cavitation.Pasadena, CA, USA, 2001.
December 26, 2009, Revised April 14, 2010)
* Project supported by the National Nature Science Foundation of China (Grant No. 10832007).
Biography:LI Jie (1977-), Male, Ph. D. Candidate, Lecturer
2010,22(3):312-318
10.1016/S1001-6058(09)60060-3
杂志排行
水动力学研究与进展 B辑的其它文章
- BROADBAND ROTOR NOISE PREDICTION BASED ON A NEW FREQUENCY-DOMAIN FOUMULATION*
- THE EFFECT OF RECLAMATION IN AREAS BETWEEN ISLANDS IN A COMPLEX TIDAL ESTUARY ON THE HYDRODYNAMIC SEDIMENT ENVIRONMENT*
- IMPROVED DEM-CFD MODEL AND VALIDATION: A CONICAL-BASE SPOUTED BED SIMULATION STUDY*
- FLOWS THROUGH ENERGY DISSIPATERS WITH SUDDEN REDUCTION AND SUDDEN ENLARGEMENT FORMS*
- NUMERICAL SIMULATIONS OF WAVE-INDUCED SHIP MOTIONS IN TIME DOMAIN BY A RANKINE PANEL METHOD*
- SENSITIVITY STUDY OF THE EFFECTS OF WAVE-INDUCED VERTICAL MIXING ON VERTICAL EXCHANGE PROCESSES*
