液面上大气泡形状的热力学证明

王正烈

(天津大学理学院化学系 天津300072)

师生笔谈

液面上大气泡形状的热力学证明

王正烈

(天津大学理学院化学系 天津300072)

针对物理化学教材中的一道习题，对液面上形成的半球形大气泡进行分析，建立物理模型，提出简化假设，根据表面热力学原理，用数学方法给以证明，并绘出了相对表面吉布斯函数曲线。

在物理化学教材中，关于表面现象有一道习题，要求学生观察下雨时水面上形成一个大气泡的形状，并说明理由［1-3］。

可以说所有的学生均会答出液面上大气泡的形状为半球形，但是要说明并证明为何是半球形就较困难了。

1 习题解答书中对气泡为半球形的解答

在已出版的对教材［2］的习题解答书中，有几种对该问题的解答可以说完全相同。都认为气泡的形成过程基本上是恒温恒压过程;“当气泡达到稳定状态时，要力求其表面吉布斯函数值最低”，这是正确的;但认为“相同体积的气泡则以球状表面积最小”是下雨时水面上“气泡为半球状的原因”［4-7］，这样的推论不能令人信服。

相同体积气泡以球形表面积为最小，这是众所周知的事实，那么为什么气泡在水面上不是圆球形而是半球形呢?悬浮在空中的圆球形肥皂泡若落在肥皂液的表面上还会呈圆球形吗?答案应是半球形。所以仅仅从球形表面积最小来说明液面上大气泡呈半球形，其理由还不充足。

在教材［1］该题的答案中说明气泡呈半球形是因为“气泡膜的面积最小”;在教材［3］该题的答案中提示，“数学上可以证明这时气泡膜的面积最小”。这里强调的是气泡膜的表面积最小。因为在形成大气泡前后液体水平面的表面积可以认为是不变的，所以形成大气泡后，系统中新产生的表面只是气泡膜的内外表面。只要气泡膜的表面积最小，就可以使系统的表面吉布斯函数值最小。这就是教材［1］和教材［3］对该问题答案中所说气泡膜面积最小的含义。

2 本习题的意义

这道题不只是简单地让学生应用表面热力学原理解释观察到气泡为半球形是因为这时系统的表面吉布斯函数应为最低，而是希望学生能够独立思考或者在教师的启发和指导下，通过观察分析，建立模型，提出简化假设，根据表面吉布斯函数最低原理，经过数学推导，得出证明结论。这样的证明相当于一篇小的学术论文，可以对培养学生科学研究方法起到启迪作用，而且所应用的手段只是表面热力学原理，以及立体几何、微分等学过的数学知识，篇幅也不大。教师也可以把此题提前布置作为课堂讨论之用。

因为形成气泡的过程既可以认为是恒温恒压过程，也可以认为是恒温恒容过程，所以既可以应用表面吉布斯函数最低原理，也可以应用表面亥姆霍兹函数最低原理来证明气泡的形状。应当说明的是液面上的气泡只是亚稳状态，而气泡破裂消失才能真正达到热力学上最稳定的状态。

3 气泡为半球形的证明

3.1 模型的建立

在建立模型前，应观察一下液面上大气泡的实际形状，如图1。

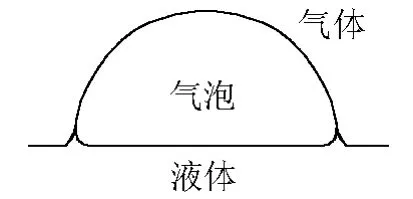
图1 液面上大气泡的实际情况

从图1可以看出，液面上的气泡并非绝对的半球形，在与气泡膜接触处，在膜内外表面的表面张力作用下，液体表面向上有所弯曲。然而正如前面指出的那样，在形成气泡后，气泡内外液体水平表面积与没有形成气泡前水平面的表面积几乎是相同的。

根据气泡的半球形状，可以建立气泡的球缺形物理模型，以水平液体表面与球缺形气泡膜交界处气泡膜的切线与液体水平表面之间通过气泡内的夹角θ为变量，如图2，以便证明半球形气泡在热力学上是相对稳定的。角θ的变化范围为0°＜θ≤180°。

3.2 简化假设

由于建立的模型与真实情况有所差异，故要做以下4个合理的简化假设:

①设气泡膜内外液体水平表面在与气泡膜交界处呈水平。这是针对实际情况该处液面向上稍有弯曲而提出的。②设重力对气泡膜的影响可以忽略，因而气泡成球缺形。③ 因曲率半径很大，设弯曲的气泡膜对气泡内气体的附加压力可不考虑，故角θ为不同值时，气泡膜内气体体积恒定，且膜内外液体表面处于同一水平。④因气泡膜很薄，设气泡膜内外两表面的面积相等。

这4个假设是为了下面计算气泡膜的面积及液体水平表面积时考虑的。其中主要是前2个假设，后2个假设因影响微乎其微，本可不必提出，但为了严谨起见，还是应当加以考虑的。

3.3 推导

i为系统中的每一种界面。本文中只有一种界面，即液体的表面。

以V代表气泡的体积，R、h分别代表球缺的球面半径及球缺的高;以Sl、Sm分别代表水平液体表面和气泡膜单面的面积，且Sl值足够大;以γ代表液体的表面张力。

角θ的变化范围为0°＜θ≤180°。当θ取不同值时，R、h均相应地改变，致气泡膜的单面面积Sm也相应地改变，因而系统的总表面吉布斯函数也相应地改变。由

及

得:

气泡膜的单面面积

因系统中水平液体表面积为S1，气泡膜有内外两个表面，且认为相等，故系统的总表面吉布斯函数为:

将式(5)代入式(6)，得:

由于气泡体积V及液体水平表面积S1均不变，液体表面张力γ为定值，故系统总表面吉布斯函数值为θ的函数。

3.4 证明

4 相对表面吉布斯函数及绘图

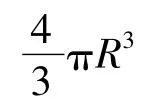
这时圆球形气泡膜的表面吉布斯函数为:

定义系统的相对表面吉布斯函数［8］

对本文讨论的系统，相对表面吉布斯函数的意义就是球缺形气泡膜的表面吉布斯函数与同体积圆球形气泡膜的表面吉布斯函数的比值。将式(7)及式(10)代入式(11)，得:

表1 球缺形气泡的相对表面吉布斯函数与角θ之间的关系

表1 球缺形气泡的相对表面吉布斯函数与角θ之间的关系

θ/° Gsrelθ/° Gsrelθ/° Gsrel10 2.4539 70 0.8214 130 0.8711 20 1.5656 80 0.8001 140 0.9060 30 1.2203 90 0.7937 150 0.9411 40 1.0376 100 0.7994 160 0.9716 50 0.9290 110 0.8154 170 0.9925 60 0.8618 120 0.8399 180 1.0000

5 总界面吉布斯函数最低原理对类似系统的应用

用系统的总表面吉布斯函数最低原理证明液面上大气泡的形状为半球形，是这一类型问题中最简单的应用。这是因为系统内只有一种表面，即液体表面。为了区分气泡膜的表面及水平液体的表面，在前面分别采用了表面积符号Sm和S1，而实际上Sm和S1均是液体的表面。所以系统内只有一种表面张力γ，而且变量只有一个角θ。

比液面上大气泡稍复杂一些的情况是一个适当小的液滴在水平的光滑固体表面上的形状。对此也采用球缺形液滴模型，虽然仍只有一个角度变量，但是存在着固-液、固-气和液-气3种界面，因而有3种界面张力。用同样的原理可以证明，在不同的界面张力组合下液滴稳定存在时的形状，并且导出了液体的接触角与3个界面张力之间的等式关系——杨氏方程［8］。

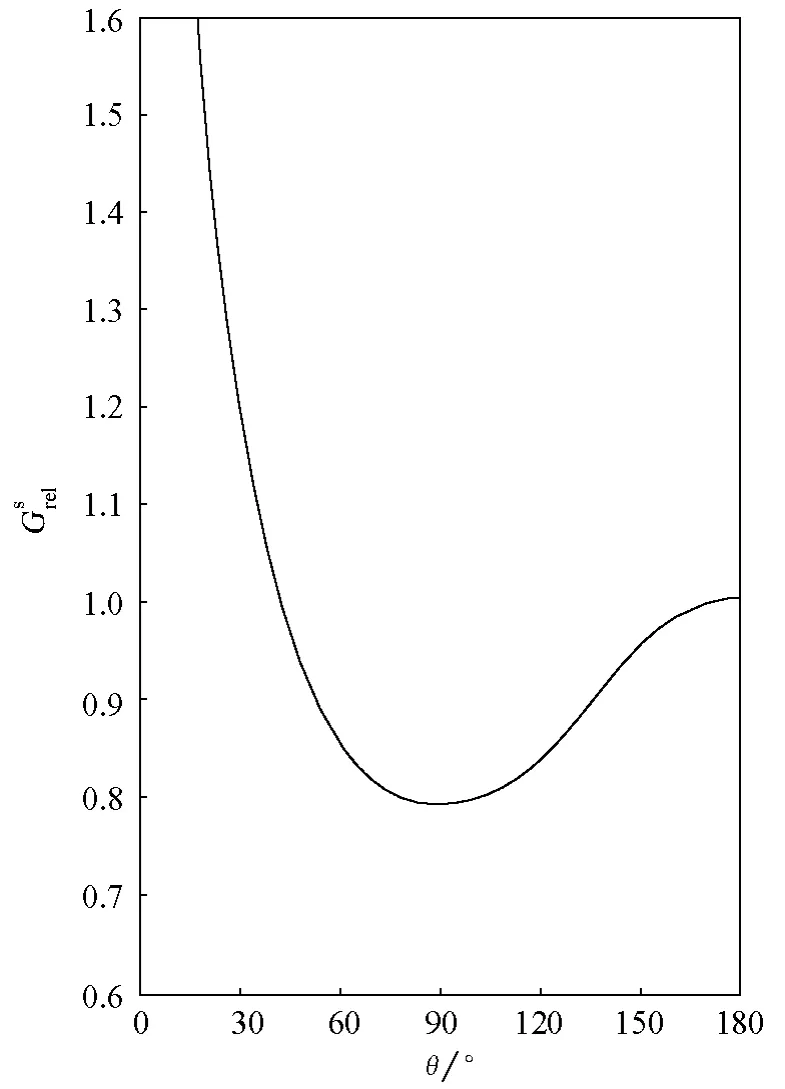
图3-θ曲线图

球形固体粒子在两不互溶液体之间的系统，有2个液相、1个固相，因而存在着3种界面张力，假想液-液界面将球形固体粒子分成两个球缺形，这时也只有一个角度变量。用同样原理可以证明，在3种界面张力满足杨氏方程时，球形粒子分配于两不互溶液体之间［9］。

更复杂一些的系统是讨论一适当小的液滴在与之不互溶的液体表面上的形状。这时系统中有2个液相、1个气相，也仍然存在3种界面，因而有3种界面张力。采用双凸透镜液滴模型，假想不互溶液体表面将此双凸透镜分成两个球缺形，但是要假设两个角度变量。用同样的原理，可以证明在不同界面张力组合下，小液滴稳定存在时的形状，并导出小液滴在不互溶液体表面上成液体透镜时，3个界面张力与两个接触角之间的等式关系——诺依曼三角形［10］。

［1］ 王正烈.物理化学.北京:化学工业出版社，1997

［2］ 天津大学物理化学教研室编.王正烈，周亚平，李松林，等修订.物理化学(下册).第4版.北京:高等教育出版社，2001

［3］ 王正烈.物理化学.第2版.北京:化学工业出版社，2006

［4］ 肖衍繁，李文斌，李志伟.物理化学解题指南.北京:高等教育出版社，2003

［5］ 金继红，何明中，金飚.物理化学习题解答(天津大学第4版).武汉:华中科技大学出版社，2005

［6］ 宋波.物理化学(第4版)同步辅导及习题全解.北京:中国矿业大学出版社，2006

［7］ 李方，薛涛，秦学.物理化学全程导学及习题全解(天津大学第4版).北京:中国时代经济出版社，2007

［8］ 王正烈.化学学报，1980，38(2):103

［9］ 王正烈.齐齐哈尔轻工学院学报，1988，4(4):12

［10］ 王正烈.高等学校化学学报，1992，13(4):525