自适应蚁群算法在YKK系列中型高压电机优化设计中的应用
2010-07-02孟大伟吕海鹏
孟大伟,吕海鹏,徐 磊
(哈尔滨理工大学,哈尔滨 150040)
1 引言
电机的优化设计可以被描述为一个复杂的有约束、非线性、混合离散多目标规划问题。在传统优化算法出现计算困难的状况下,应用现代启发式算法能有效地解决此类问题,且其计算的可并行性,可以充分利用计算机的资源[1]。
相对于小型电机而言,中型高压电机的优化设计存在着以下难点:
(1)变量的离散程度大 离散变量的存在使得大多数优化算法不能被直接使用。因此,要想将算法应用于电机设计当中,必须对算法进行适当的改进[2]。
(2)线规的选取 线规组合面积的变化规律异常复杂,而且可以选用的组合有限。因此,线规选取不当会对电机性能产生很大的影响。
(3)优化算法的选取 由于现在常用的优化算法,如模拟退火(SA)、遗传算法(GA)、蚁群算法[3,4](ACA)的全局收敛性存在差异,所以,结合电机优化设计的特点选择适合的算法显得尤为重要。
本文重点介绍了ACA的基本思想及其特点,并结合电机优化的问题,详细论述了蚁群算法在电机优化设计中的具体实现方法,最后将其应用到了YKK系列电机的优化设计,取得了较好的效果。
2 蚁群算法简介
2.1 基本蚁群算法
现以求解典型的旅行商问题(Traveling Salesman Problem,TSP)为背景,说明蚁群系统模型。
TSP可以形象地描述为:假设平面上有n个城市,n个城市的TSP问题就是寻找通过n个城市各一次且回到出发点的所有路径中最短的一条。
蚂蚁从起始城市开始在相邻城市之间转移,直到达到目标状态完成一次解的搜索。信息素强度是蚂蚁进行城市间转移的依据。每只蚂蚁的转移是根据转移概率随机进行的。从城市i转移到某个相邻城市 j的转移概率为:
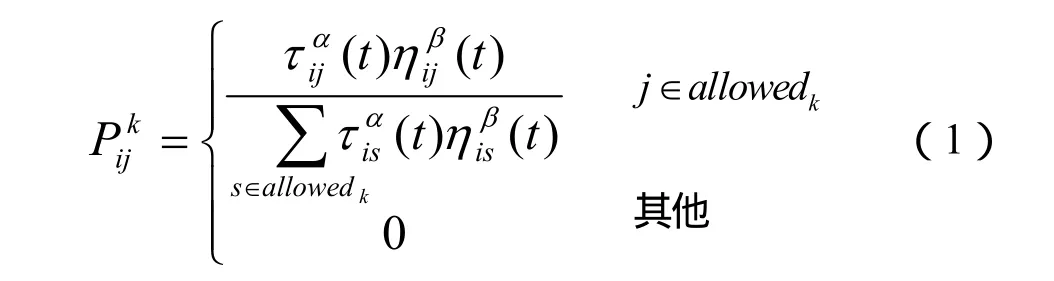
式中,τij(t)是t时刻搜索时城市i和j之间的信息素强度;α和β是大于零的参数;ηij是城市 i和j之间距离的倒数,是一种启发信息;allowedk={1,2,…,n-1}表示蚂蚁下一步允许选择的城市。随着时间的推移,以前留下的信息逐渐流逝,用参数1-ρ表示信息消逝程度,经过n个时刻,蚂蚁完成一次循环,各路径上信息量要根据下式进行调整:
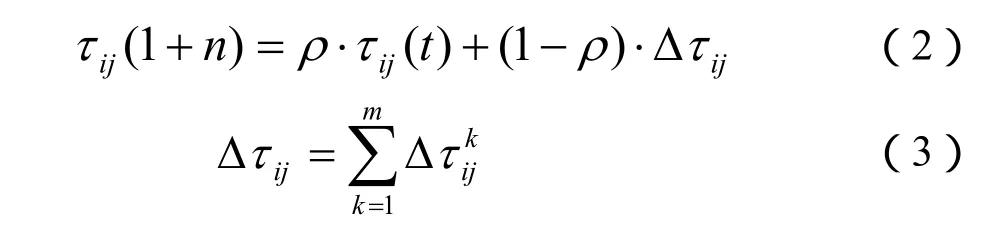

其中,Lk表示第 k只蚂蚁在本次循环中所走过路径的长度。
2.2 算法参数的选择
几乎所有的模拟进化算法的优化性能都与参数的选择密切相关,不同的参数选择对优化算法的影响很大。针对本文系列电机的优化,算法的参数选择如表1所示。

表1 蚁群算法主要参数
3 系列电机串行优化设计的数学模型
一般,系列电机的优化设计多采用并行算法的思路,本文采用串行计算思路。串行优化设计也称降维优化设计,即将复杂多规格共冲片电机设计问题转化为单规格电机优化设计问题。其单规格电机优化数学模型可描述为以下问题的极值:
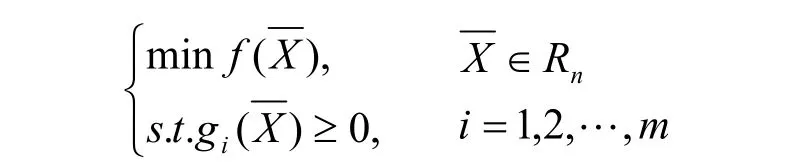
3.1 优化设计的目标函数
由于目标函数的建立是影响着优化设计向何处去的关键且本课题的主旨是“节能”,因此本文选择效率为目标函数。可表示为
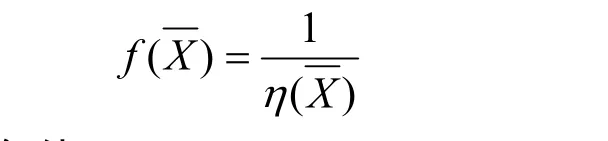
3.2 约束条件
约束条件可分为两类,一类为基本约束条件;另一类为一般约束条件。
基本约束条件为电机性能要求,即效率、功率因数、起动转矩、最大转矩、 起动电流以及热负荷,具体可表示为
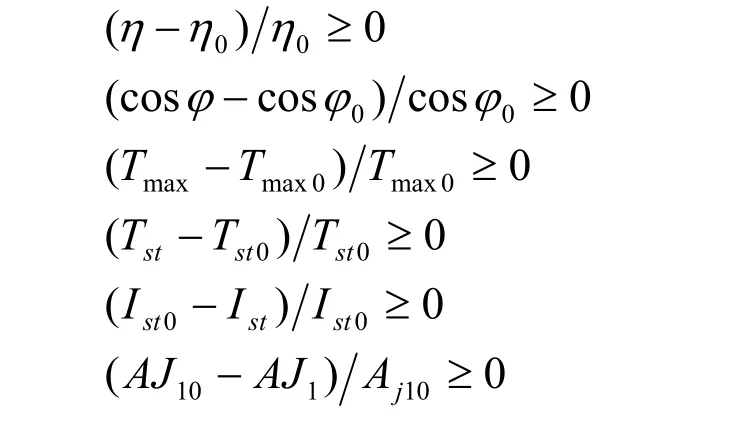
下标带“0”者为相应标准值。
一般性约束条件包括优化变量的非负约束,且多为强制性约束,如本文中的几何尺寸约束:
(1)对线规的约束
本文所用线规的宽边和窄边尺寸均在企业所规定的扁线限用表内选取。
(2)定子槽型尺寸与线规应满足的约束

其中:Na为导体纵向并排个数;a为导体绝缘后高度;si为松散量;Z1为槽内导体数;tmi为主绝缘厚度;sj为层间垫条厚度;hs2为定子槽有效高度;Nb为导体横向并排个数;b为导体绝缘后宽度;bs1为定子槽宽度。
(3)对槽楔的约束
当定子槽楔的宽b≥14mm时,槽楔厚度为5mm,否则为4mm;槽楔的相对磁导率为4µ0。
3.3 优化变量
系列电机设计中最重要的特点之一就是若干规格的电机采用相同的定、转子冲片。因此,共冲片电机设计须将设计变量分为两类:一类是公用变量'X,包括各规格电机相同的变量,例如本文选择的定子槽宽bs1,定子槽高hs2,转子槽宽br1、转子槽高hr2;另一类是非共用变量''X,包括各规格电机可以各自独立变化的变量,本文选择的铁心长度L、槽内导体数Z1、线规尺寸均为非共用变量。
3.4 串行优化法的实现
串行优化法首先需要人为地从多规格中选出一个重点规格。本文选择功率最大的电机为重点规格,以其效率最高为目标,按全部设计变量进行优化设计。得出该规格的优化方案后,则固定“公用变量”值,而针对“非公用变量”对其他各规格电机逐一优化。如有不够理想的方案,可以适当调整后再重复上述计算,直到全部规格满足要求为止。
4 蚁群算法的改进及其在电机优化设计中的应用
4.1 改进的自适应蚁群算法
电机优化设计问题规模比较大,由于信息量的挥发系数ρ存在,使那些从未被搜索到的信息量会减小到接近于0,降低了算法的全局搜索能力。根据公式(1)和(2),解的信息量随着ρ的增大而增大,以前搜索过的解被再次选择的几率就大,收敛速度也就越快,从而降低了到算法的全局搜索能力。然而,减小ρ虽然可以提高算法的全局搜索能力,但又会使算法的收敛速度降低。因此可以自适应地改变ρ的值。ρ(t0)=1;当算法求得的最优值在N次循环内没有明显改进时,ρ减为
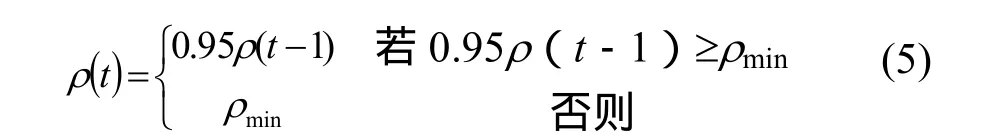
其中ρmin为最小值,可以防止ρ过小降低算法的收敛速度。本文N和ρmin分别选为50和3。
4.2 蚁群算法在电机优化设计中的应用
对于电机优化设计,选择一个合适的算法固然重要,但更重要的是结合电机设计的特点对算法进行适应性的改进并应用到设计当中。本文算例涉及的中型高压系列电机优化设计具备如下特点[5]:
(1)电机属于系列化产品,出于管理与经济上的原因,对极数相同、容量相近的电机采用共冲片设计。因此,这类优化设计中的优化变量有共用与非共用之分;
(2)电机参数的非连续性要求其变量搜索必须按离散方式进行,以使优化空间的任一探测点都能满足工程实际的需求;
(3)优化目标函数与约束函数的相悖性,常使得电机优化设计的最优点位于边界上;
(4)电机设计数值函数是非线性程度很高的复杂问题,必须协调好全局寻优与收敛速度之间的矛盾。
结合上述特点,电机优化程序流程如下:
(1)构建路径
首先,将设计变量转化为优化变量,并构成蚁群算法中蚂蚁的可行域。可行域以矩阵的形式存在,如图1所示。
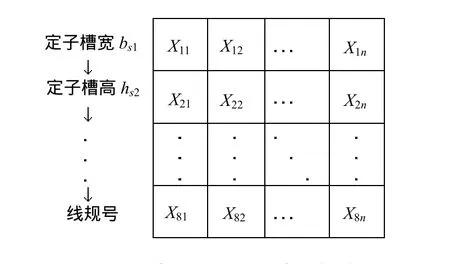
图1 优化变量所组成的矩阵
(2)对约束条件进行处理
目标函数f(x),服从于gi(x)≥0,i=1,2,…m,其中m是约束的数量。然后,可将等价的非约束优化问题描述为
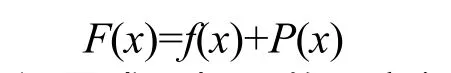
将惩罚函数设置成目标函数,它惩罚任何对于约束的违背,强迫非约束优化朝着可行的区域进行。惩罚函数P(x)定义如下
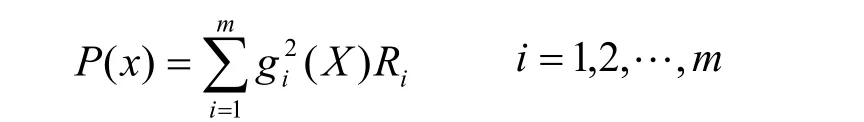
式中Ri是惩罚参数,被认为是惩罚因子。按约束违背的水平,相应地变化Ri。
(3)构建信息素矩阵
信息素τij表示当蚂蚁从第i行变量选择第j行变量的期望度。它也以矩阵的形式存放,与变量矩阵相对应,如图2所示。
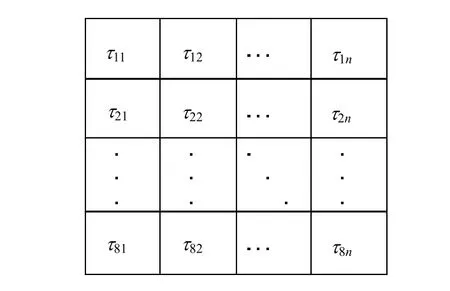
图2 信息素矩阵
(4)启发式信息
α的大小表明每个路径上信息量的受重视程度,α值过大会使搜索过早陷于局部最小点。β的大小表明启发式信息的受重视程度。本文对α和β得选择参照表1。
(5)解的构建
蚂蚁根据公式(1)计算出的概率从其可行邻域(即所有蚂蚁k还没有访问过的变量)中选择下一个变量,逐步完成对每个优化变量的选择。将选择出的优化变量通过接口转化为设计变量送入主程序完成电磁核算并进行方案评估。
(6)信息素更新
根据公式(2)、(3)、(5)更新信息素矩阵。
(7)检验是否符合结束条件,如果当前的迭代次数达到了预先设定的最大次数,则停止迭代,输出最优解,否则转到(2)。
5 算例及分析
应用如表1所选参数的自适应蚁群算法对YKK系列高压三相异步电动机进行优化。计算符合以下条件:
(1)不变动统一设计的系列型谱以及对相同极数和同一机座号共用定、转子冲片的原则;
(2)统一设计中的定转子内、外径尺寸和轴尺寸以及定、转子槽的形状不允许改变,不能任意更动槽配合;
(3)铁心材料为w400硅钢片;
(4)槽楔磁导率µ=4µ0;
(5)风摩耗值仍以统一设计值为依据。
表2和表3列出了YKK500-2共冲片三个规格电机(2000kW、2240kW、2500kW)结果对比情况。
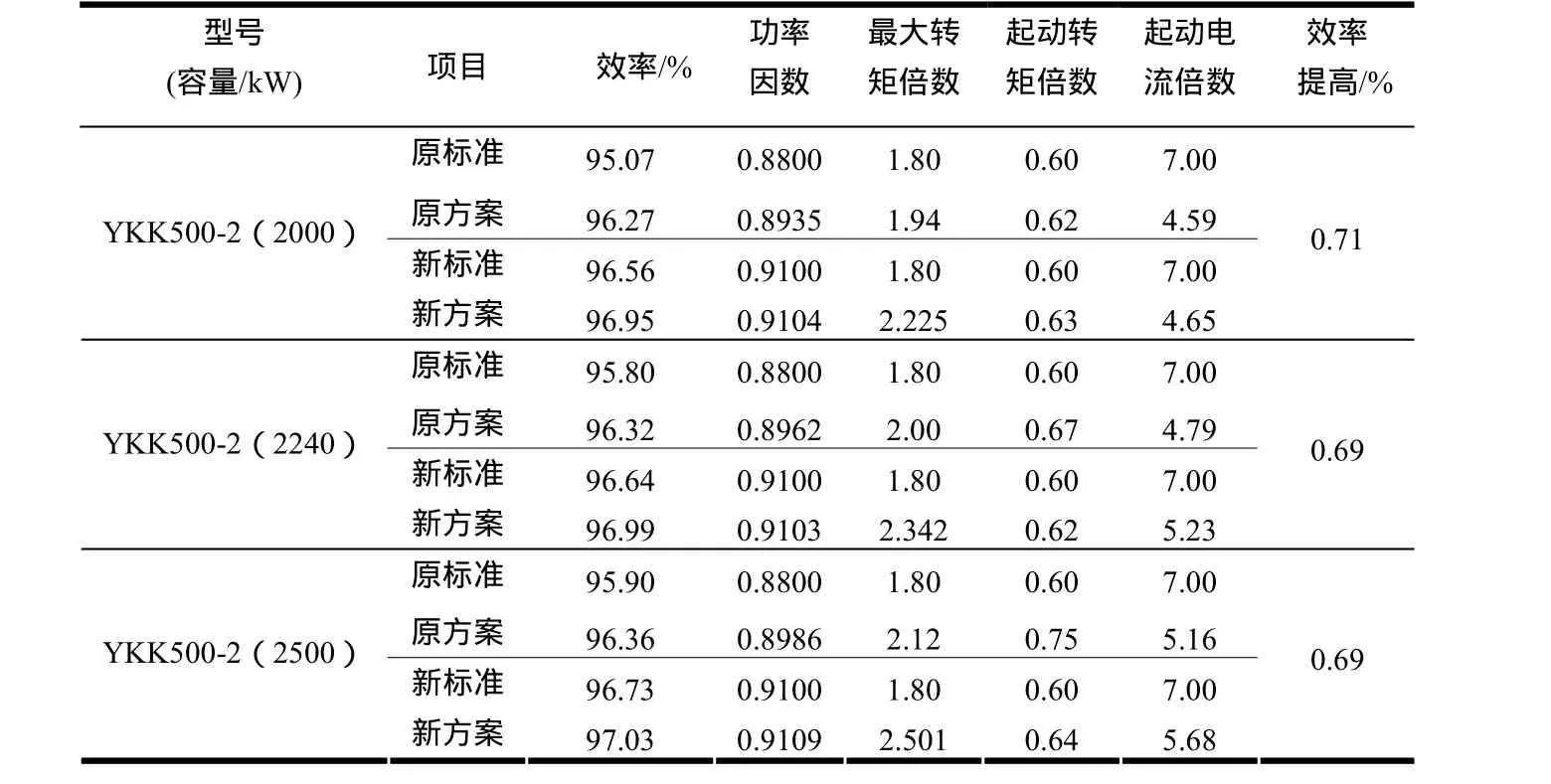
表2 性能指标对比

表3 有效材料用量
5.1 性能指标分析
分析表2的性能指标表明:原方案的效率和功率因数均不能满足新设计标准,而采用自适应蚁群算法优化过的新方案则完全满足标准,效率分别提高了0.71%、0.69%、0.69%,均有一定的设计裕度。最大转矩倍数的平均值为2.356,比原方案的最大转矩倍数平均提高16.63%。
5.2 经济指标分析
表3所示三种规格电机,中心高由原来的560降为新设计方案中的500,D1/Di1由原来的990/560变为现在的900/500,体积有了明显的缩小,线规尺寸较原方案也有了很大的缩小,有效材料用量有了很大程度的节省。
新设计方案定子绕组用铜平均节约14.86%,硅钢片用量平均节约18.14%。
6 结论
本文结合电机设计的特点及工程实际对蚁群算法做了改进。经过实例计算表明,效率、功率因数和最大转矩有所提高,优化结果令人满意。因此,算法具有工程实际意义。
[1]张善儿,陈世元.现代电机优化设计启发式算法[J].微特电机,2006,1(2):94.
[2]孟朔,赵争鸣.异步电机的优化设计新方法[J].清华大学学报(自然科学报).2001,41(6):120-123.
[3]M Dorigo,L M Gambardella.Ant Colony System:A Cooperative Learning Approach to the Traveling Salesman Problem[J].IEEE Trans.On Evolutionary Computation,1997,1(1):53-66.
[4]M Dorigo,G Di Caro.The Ant Colony Meta-heuristic.In:D Corne.M Dorige,F Golver( Eds.) New Ideas in Optimization,McGraw-Hill[M]. New York,1999.11-32.
[5]孟大伟,周美兰.模拟退火算法在电机设计中的应用[J].电机与控制学报, 2001, 5(3).
