准直孔对三探测器法密度测井精度影响的MC模拟研究

吴文圣 肖立志

(油气资源与探测国家重点实验室，中国石油大学 北京 102249)

我国绝大多数油田属于陆相沉积，薄互层多且层中油气资源丰富。在油田的高含水后期开发阶段，为持续稳产，薄差储集层成为增加油气产量的重要开采对象。因此，需研究能分辨厚度为20 cm左右薄储层的测井方法，其中，高分辨率密度测井必不可少。高分辨率密度测井也称多探测器密度测井，系在双源距密度测井基础上发展。在双源距密度测井仪上增加探测器的方法有：(1) 在负源距范围内增加一个探测器[1]；(2) 在原来的长、短源距探测器间增加一个中间源距探测器[2]。方法(2)较方法(1)的伽玛屏蔽要求低、成本低，更具可行性。密度测井要求高分辨率、高精度，因此需优化仪器结构设计，其中包括γ源和探测器准直孔形状和开口角度的优化设计[3]。本文用 Monte Carlo通用计算程序MCNP[4,5]研究γ源和探测器准直孔形状和开口角度对高分辨率密度测井测量精度的影响。

1 计算模型

模型建立为半圆柱状[6,7](图1)，地层高75 cm，半径为33 cm。仪器推靠井壁，外壳及源仓材料是钢，探测器承压壳为镉。γ源为137Cs点源，能量0.662 MeV，源和探测器之间为理想屏蔽体。探测器记录能量>0.15 MeV光子，并使统计误差<1%。

图1 计算模型Fig.1 The MC simulation model.

2 γ源的准直孔形状

密度测井中，γ源和探测器在油井的同一侧，探测器的地层散射γ计数与γ源的准直孔形状有关[8]。现有密度仪γ源基本都采用图2所示楔形和窗形准直孔，图中ψ为γ源准直孔开口角度。

由图3，对窗形和楔形γ源准直孔，探测器计数均随准直孔开口角度增大；对高密度纯灰岩与40%孔隙度含水石灰岩，两种形状的准直孔所得的探测器计数差别很小。因此，仅由探测器计数率的大小，不易区分两种形状准直孔的优劣。

图2 辐射源准直孔形状Fig.2 The collimation aperture shape of radioactive source.

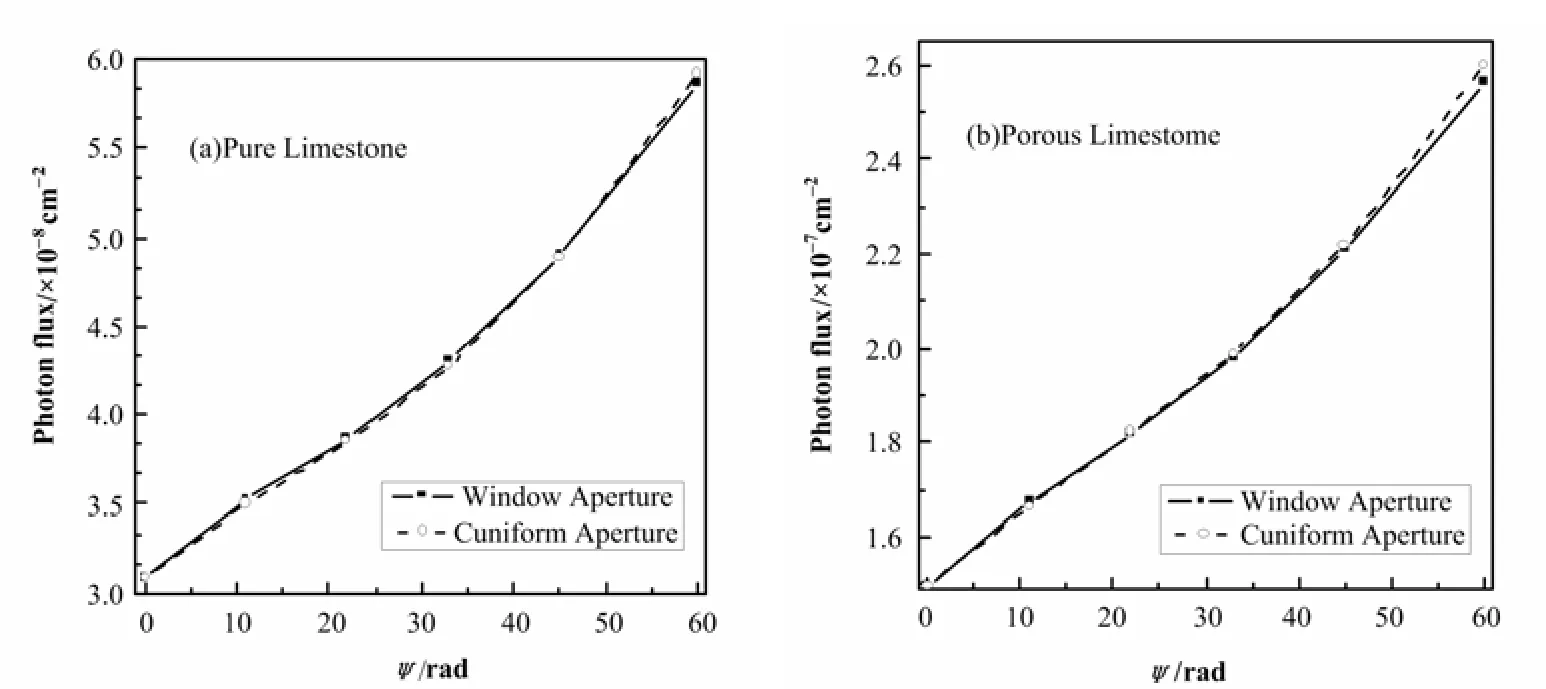
图3 探测器计数与γ源准直孔开口角度的关系Fig.3 Scattering γ-ray counts from different formations vs the opening angle of the γ-ray source aperture.

由图 4，随着准直孔开口角度的增大，两种情况下探测器的灵敏度均降低。比较而言，在准直孔开口角度一定时，楔形准直孔时的探测器灵敏度高于窗形。因此，可选择楔形准直孔作为γ源的准直孔开口形状。

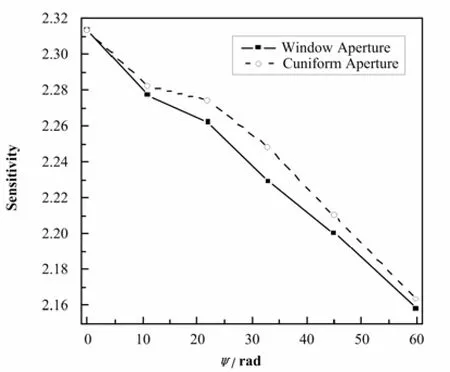
图4 探测器灵敏度与γ源准直孔开口角度的关系Fig.4 The detector sensitivity vs the opening angle of the γ-ray source aperture.

3 γ源的开口角度及探测器准直孔形状和开口角度

3.1 γ源准直孔开口角度

密度测井中，须保证长源距探测器具有足够大的计数率，从而有足够的测量精度，这是在确定 γ源准直孔开口角度时必须考虑的。

计算时，设长源距为37 cm，探测器准直孔开口形状有窗形、楔形和槽形(图5)，图中θ为探测器准直孔开口角度。γ源和探测器准直孔开口角度均按 0°、11°、22°、33°和 45°变化，计算结果见图 6、图7，两图中N和A分别表示计数率和探测器对地层的灵敏度。

由图6，窗形、楔形或槽形探测器计数率均随γ源准直孔开口角度增大，增长幅度较快；当γ源开口角度一定时，计数率随探测器开口角度变化的幅度很小，甚至可以不考虑。可见，在对探测器的计数率贡献中，γ源准直孔开口角度处于绝对主导地位。

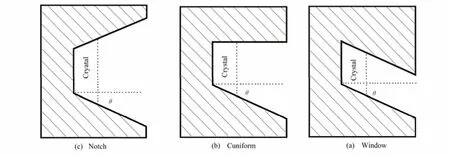
图5 三种形状的探测器准直孔Fig.5 Detector opening shapes.

图6 纯灰岩中长源距探测器计数率与探测器和γ源开口角度的关系Fig.6 The relationship between long-spacing detector count and the opening angle of source in pure limestone.

图7 长源距探测器灵敏度与探测器和γ源开口角度的关系Fig.7 The relationship between long-spacing detector sensitivity and the opening angle of source.

由图 7，对窗形、楔形或槽形准直孔，长源距探测器对地层密度灵敏度均随着γ源开口角度增大而减小；当源窗开口角度一定时，灵敏度随探测器开口角度呈一定变化，但其对灵敏度的影响程度明显小于源窗开口角度对灵敏度的影响。γ源准直孔开口角度从0°–45°，灵敏度变化程度不超过6%。

综合图6和图7，γ源开口角度对长源距探测器的灵敏度影响较小，对计数率影响很大。对长源距探测器，得保证计数率有足够好多统计误差。因此，高分辨密度测井的γ源开口角度以45°为宜。

3.2 长源距探测器的开口形状和角度

选择长源距探测器准直孔形状和开口角度应以计数率为主要考虑对象，兼顾考虑灵敏度。由图6、图 7，不同开口角度的三种形状探测器准直孔对探测器计数率的影响很小，因此，探测器准直孔可以是窗形、楔形和槽形中的任意一种，为减少井眼对探测器的影响，探测器准直孔开口角度以0°为宜。

3.3 中源距探测器的开口形状和角度

设中源距为21 cm，由图8，窗形、楔形或槽形探测器的计数率均随γ源开口角度增大，增长幅度较快，趋势稳定；当γ源开口角度一定时，计数率随探测器开口角度增加，增幅较小。可见，γ源窗开口角度对探测器计数率的贡献仍处于主导地位。

图8 纯灰岩中中源距探测器计数率与探测器和γ源开口角度的关系Fig.8 The relationship between middle-spacing detector count and the opening angle of source or detector in limestone.

由图 9，三种形状的中源距探测器对地层密度灵敏度均随γ源开口角度的增大而减小，减小幅度较快；当γ源开口角度一定时，灵敏度随探测器开口角度的变化幅度不大。探测器开口角度变化对灵敏度的影响明显小于γ源开口角度的影响。

图9 中源距探测器灵敏度与探测器和γ源开口角度的关系Fig.9 The relationship between middle-spacing detector sensitivity and the opening angle of source.

图8、9显示，γ源开口角度45°、三种形状准直孔开口角度5°–15°时，探测器计数率和灵敏度均较大。为减少井眼影响，准直孔形状以窗形为佳。因此，探测器为窗形，开口角度为5°–15°时，中源距探测器将有较高的测量精度。

3.4 短源距探测器的开口形状和角度

图10 纯灰岩中短源距探测器计数率与探测器和γ源开口角度的关系Fig.10 The relationship between short-spacing detector count and the opening angle of source or detector in limestone.

图10、11是短源距为10.5 cm时的计算结果，三种形状准直孔探测器的计数率均随γ开口角度增大，增长幅度较快，趋势稳定；当源窗开口角度一定时，计数率随探测器开口角度增加的幅度明显大于中源距和长源距的情况。由于短源距探测器有足够大的计数率，计数率不是影响测量精度的主因。短源距探测器的源距较小，对地层的灵敏度较小，提高灵敏度是选择探测器开口形状和开口角度所要考虑的首要因素。

图11 短源距探测器灵敏度与探测器和γ源开口角度的关系Fig.11 The relationship between short-detector sensitivity and the opening angle of source.

图11中三种形状准直孔的短源距探测器对地层密度灵敏度均随γ源窗开口角度的增大而减小，幅度减小较快；当γ源窗开口角度一定时，灵敏度随探测器开口角度的变化幅度不一，槽形变化幅度较小，窗形和楔形变化较大。当γ源开口角度为45°时，窗形和楔形的探测器灵敏度随开口角度的变小而增大，开口角度为零时，灵敏度最大，因此，短源距探测器的开口角度为0°，即探测器为窗形准直孔。

4 结论

γ源的准直孔形状和开口角度对测量精度的影响远大于探测器准直孔形状和开口角度；γ源和探测器的准直孔形状和开口角度对计数率的影响远大于对地层灵敏度的影响。为使高分辨率密度测井仪达到较高的测量精度，γ源的形状以楔形，开口角度 45°为宜；长源距探测器准直孔形状和开口角度以窗形，0°为宜；中源距探测器准直孔形状和开口角度以窗形，5°–15°为宜；短源距探测器准直孔形状和开口角度以窗形，0°为宜。

1 Eyl K A, Chapellat H, Chevalier P,et al. Soc Pet Eng,SPE-28407, 1994: 467–480

2 Stoller C, Darling H L, DasGupta T,et al. Density logging in slim holes with a novel array density tool, In: SPE Annual Technical Conference and Exhibition, SPE38650,1997

3 钟振千, 何清源, 王瑞平. 岩性密度测井及应用. 北京:石油工业出版社, 1994. 5–60 ZHONG Zhenqian, HE Qingyuan, WANG Ruiping.Litho-density logging and its use. Beijing: Petroleum Industry Press, 1994. 5–60

4 裴鹿成, 张孝泽. 蒙特卡罗方法及其在粒子输运中的应用. 北京: 科学出版社, 1980. 5–50 PEI Lucheng, ZHANG Xiaoze. Monte Carlo method and its use in particletransport. Beijing: Science Press, 1980.5–50

5 Briesmeister J F (Ed.). MCNP-A General Monte Carlo Code for Neutron and Photon Transport, Version 3A,Monte Carlo Section, Los Alamos Radiation Transport Group, 1986

6 吴文圣. 用Monte Carlo方法模拟三探头核测井响应及数据处理方法. 山东: 中国石油大学, 2002. 51–102 WU Wensheng. Simulating Three-Detector Nuclear Logging Response and Data Process Method with Monte Carlo Method. Doctor Thesis, Shandong: China University of Petroleum, 2002. 51–102

7 吴文圣, 黄隆基.地球物理学报, 2004, 47(1): 164–170 WU Wensheng, HUANG Longji. Chinese J Geophys,2004, 47(1):164–170

8 黄隆基. 放射性测井原理. 北京:石油工业出版社,1985. 81–100 HUANG Longji. The principle of radioactive logging.Beijing: Petroleum Industry Press, 1985. 81–100