灰色GM（1，1）模型在干旱预测中的应用

魏光辉

（新疆农业大学 水利与土木工程学院，乌鲁木齐 830052）

灰色系统理论［1］是80年代初由我国著名学者邓聚龙教授提出的。它把一般系统论、信息论、控制论的观点和方法延伸到社会、经济、生态等抽象系统，并结合数学方法，发展成为一套解决信息不完备系统即灰色系统的理论和方法。应用该方法对各种自然灾害进行预测，是减轻灾害和作出科学决策的重要措施之一。本文以蚌埠市气象站气象站27a的实测年降雨量资料，用灰色系统理论GM（1，1）对未来干旱灾害进行预测。干旱预测严格说是异常值预测，主要是干旱灾害出现时间的预测，即干旱出现的年份。预测过程是建立在实测数据和严格的数学基础上的，预测结果可作为在实际工作中的参考。

1 灰色系统预测模型理论

灰色系统理论认为一切随机量都是在一定范围内、一定时段上变化的灰色量及灰色过程，对灰量数据通过一定方式处理后使其成为较有规律的时间序列数据，再建立模型［1］。灰色系统GM（1，1）预测模型是一阶、一个变量的微分方程模型，适合于对系统行为特征值大小的发展变化进行预测。灰色GM（1，1）模型［2-4］是将随机数经生成后变为有序的生成数据，然后建立微分方程，寻找生成数据的规律，再将运算结果还原的一种方法，其基础是数据的生成。常用的生成方式有累加生成和累减生成。

1.1 GM（1，1）模型的数列预测原理

设某原始序列：X（0）={X（0）（1），X（0）（2），…，X（0）（n）}

对其进行一次累加生成，得到生成序列：

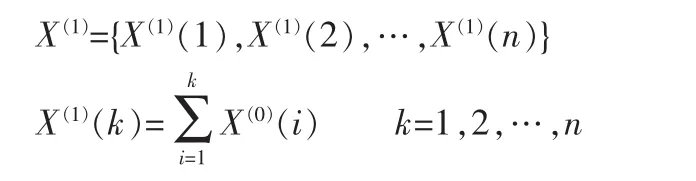
则GM（1，1）模型相应的微分方程为：

式中 α为发展灰数，α的可容区为（-2，2）；μ为内生控制灰数。

1.2 α赞为待估参数向量，可利用最小二乘法求解

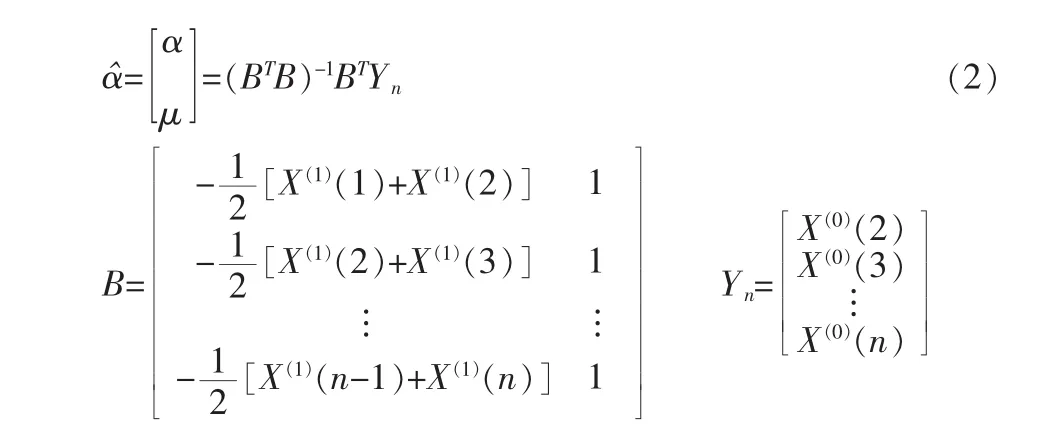
求解微分方程，得预测模型：

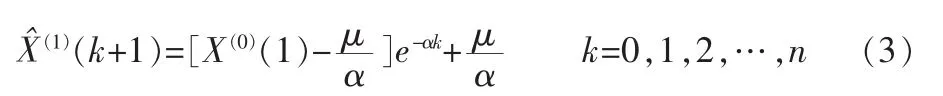
累减还原得：

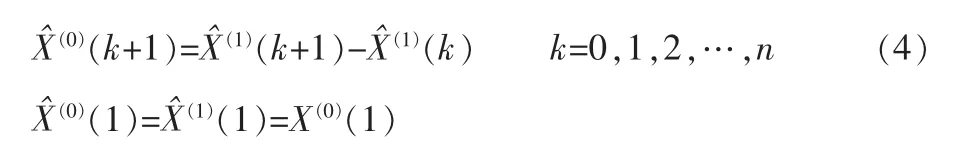
式（3）、（4）即为GM（1，1）模型进行灰色预测的基本计算公式。

1.3 模型残差检验和后验差检验［5-7］

1.3.1 残差检验

残差检验就是计算相对误差，以残差的大小来判断模型的好坏。

则ε（k）越小越好，p越大越好，一般要求ε（k）<20%，p>80%；最好是ε（k）<10%，p>90%。 X（0）为原始数据列，X赞（0）是预测数据列。

1.3.2 后验差检验

后验差比：C=S2/S1

式中 S1为原始数列的X（0）均方差；S2为残差序列{Δ（k）}的均方差；C越小，模型越好。

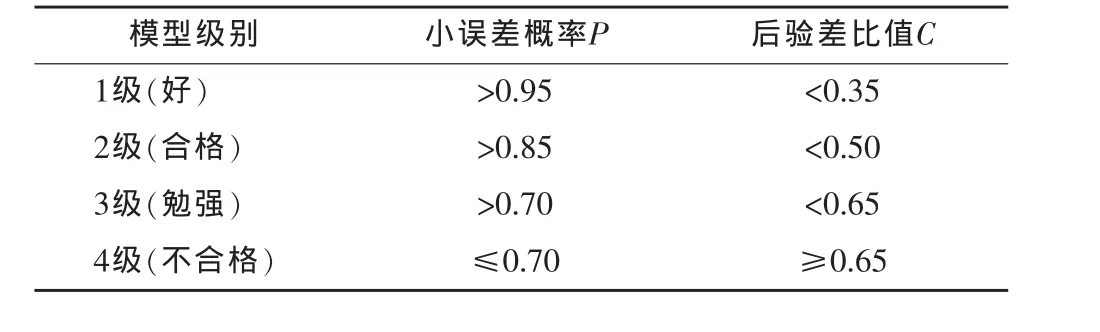
表1 检验指标等级标准

2 应用分析

蚌埠市降水量年际变化较大，在偏枯和枯水年份，蚌埠市水资源较为紧缺，严重影响本地区经济发展。因此对蚌埠市年降水量进行预测分析有着非常重要的意义。

本文采用蚌埠市气象站1980～2006年多年降水量资料，见表2。

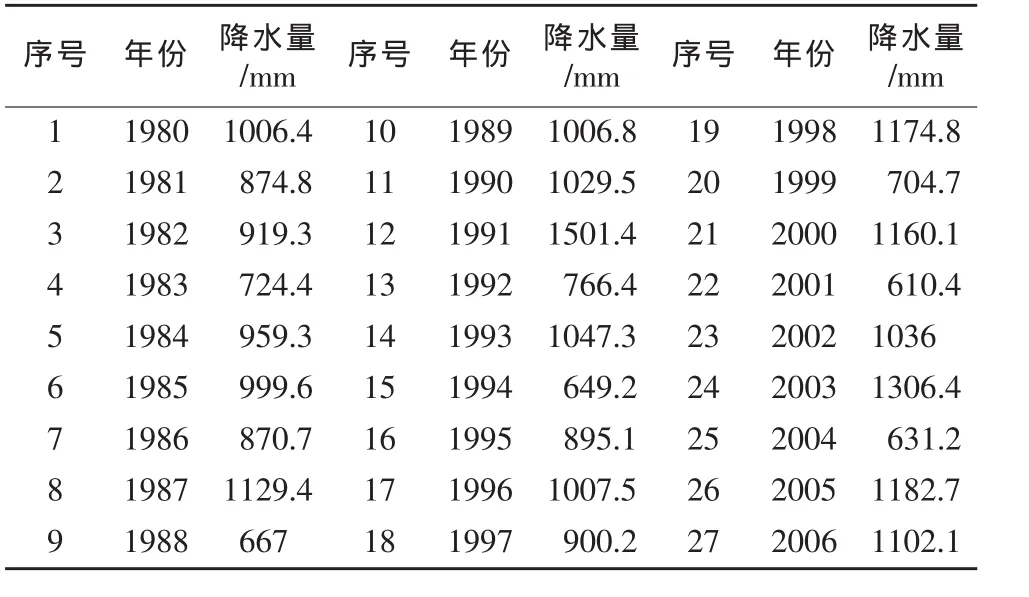
表2 蚌埠市1980～2006年降水量统计

2.1 干旱年阈值的确定

根据鞠笑生、孙荣强等人的理论［8］，判断一个地区某一年份是否为干旱年，可由参数Ipa决定：

式中 pi为某年年降水量（mm）为序列平均年降水量（mm）。

一般地，把某一地区Ipa≤-20%作为判别干旱的标准。把符合这一标准的年份挑选出来，定为干旱年。由式（5）可以求得干旱年降水量阈值为766.3mm，即年降水量小于766.3mm的年份为干旱年，由此可以得到该地区的干旱年序列X（0）（k）。

2.2 GM（1，1）模型的建立

（1）建立干旱年累加生成序列。 对X（0）（k）做一次累加求得一次累加序列，结果见表3。

表3 一次累加生成数列

（2）采用最小二乘法求解参数α与μ

依据灰色模型原理建立GM（1，1）模型，并求得模型参数：α=-0.250604，μ=8.605972，最终得模型计算式为：

X赞（0）（k+1）=38.3409e0.250604（k+1）-38.3409e0.250604kk≥1

利用建立残差模型方法进行修正，求得残差模型参数：α=0.241724，μ=0.538704，最终得残差模型计算式为：

ε赞（0）（k+1）=-1.9271e-0.241724（k+1）+1.9271e-0.241724kk≥1

将上述两式相加即得到残差修正GM（1，1）模型：

X赞（0）（k+1）=38.3409e0.250604（k+1）-38.3409e0.250604k-1.9271e-0.241724（k+1）+1.9271e-0.241724kk≥1

2.3 模型检验

2.3.1 残差检验

经检验，相对误差值为-1.30%～0.78%，见表4。

表4 模型拟合及误差计算

其残差平均值0.63%<10%，平均精度p=99.37%>95%，模型拟合精度较高，模型判为优。

2.3.2 后验差检验

经计算，后验差比值C=0.0198<0.35，小误差概率P=1，模型级别为好。

2.4 灾变点预测

模型经检验达到精度要求后，可以进行外推预测，未来蚌埠市干旱年预测结果，见表5。

由表5预计未来3个干旱年在2012年、2021年与2032年。

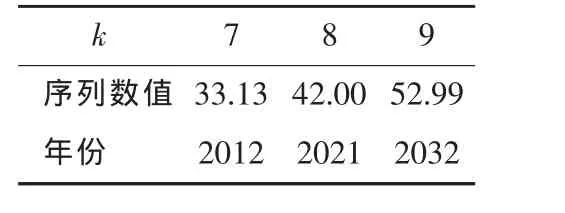
表5 蚌埠市未来干旱年预测

3 结语

灰色模型作为一种预测理论在各行各业得到充分应用。由于GM（1，1）模型要求数据较少，原理简单，计算量适中，预测精度较高等诸多优点。但需要指出的是GM（1，1）适合于短期的预测，不能用于较长时间的预测，否则会产生较大的偏差。要对较长时段的趋势值进行预测，需要引入新参数，才可以确保预测的可靠性。另外原始序列本身规律的好坏，也将影响预测模型的预测能力。

根据灰色理论建立灾变模型预测干旱年的预测过程是建立在严格的数学基础上的，预测结果可做为农业抗旱工作的参考。

［1］邓聚龙.灰色系统基本方法［M］.武汉：华中理工大学出版社，1987.

［2］刘俊民.灌区地下水年最高水位的灰色预测［J］.地下水，1993，15（3）：93-96.

［3］张大海，江世芳.灰色预测公式的理论缺陷及改进［J］.系统工程理论与实践，2002，22（8）：140-142.

［4］邱淑芳，王泽文.灰色GM（1，1）模型背景值计算的改进［J］.统计与决策，2007（3）：129-131.

［5］王劲松，郭江勇，周跃武，等.干旱指标研究的进展与展望［J］.干旱区地理，2007，30（1）：60-65.

［6］任焕莲.基于灰色GM（1，1）模型的城市需水量预测研究［J］.水利建筑与工程学报，2007（2）：52-54.

［7］张艳芳.基于GM（1，1）的残差修正模型及应用［J］.水科学与工程技术，2005（6）：51-53.

［8］孙凤华，袁健.辽宁省近50年降水序列变化规律及干旱预测［J］.气象，2004（6）：32-34.