小区进行多边形划分方法的改进
2010-06-26岳军
岳 军
(中国移动通信集团设计院有限公司 北京 100080)
1 现有小区区域划分的方法
现有小区划分算法是主要是分别进行Delaunay三角形生成,Voronoi图生成,方向角平分线剖分这三个步骤。以下先将现有的划分方法进行介绍。
1.1 Delaunay三角形生成
以独立站点位置信息参与计算生成Delaunay剖分三角形。
三角剖分的数学定义为:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段,E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件以下条件:
(1)除了端点,平面图中的边不包含点集中的任何点;
(2)没有相交边;
(3)平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包(点集的凸包是指一个最小凸多边形,满足的点或者在多边形边上或者在其内)。
最常用的三角剖分是Delaunay三角剖分,它是一种特殊的三角剖分,它需要满足2个准则,分别为:
(1)空圆特性:Delaunay三角网是唯一的(任意4点不能共圆),在Delaunay三角形网中任一三角形的外接圆范围内不会有其他点存在。
(2)最大化最小角特性:在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲,Delaunay 三角网是“最接近于规则化的”的三角网。具体的说是指在两个相邻的三角形构成凸四边形的对角线,在相互交换后,六个内角的最小角不再增大。
根据它的准则可以推断Delaunay剖分所具备以下的优异特性:
(1)最接近:以最近临近的三点形成三角形,且各线段(三角形的边)皆不相交。
(2)唯一性:不论从区域何处开始构建,最终都将得到一致的结果。
(3)最优性:任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么两个三角形六个内角中最小的角度不会变大。
(4)最规则:如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
(5)区域性:新增、删除、移动某一个顶点时只会影响临近的三角形。
(6)具有凸多边形的外壳:三角网最外层的边界形成一个凸多边形的外壳。
以上特性决定了很容易通过现有的Delaunay来进行相邻站点的判断,而且它的特性决定了算法实现的效率很高。
在站点划分中可以理解每一端点都是一个独立站点,过每一点的所有线段的另外一侧端点组成了当前站点的第一圈紧邻站点,这一部分的结果为随后的Voronoi剖分提供基础。
1.2 Voronoi图生成
Voronoi图,又叫泰森多边形或Dirichlet图,它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点,按照最邻近原则划分平面;每个点与它的最近邻区域相关联。
在站点区域划分中使用的直线即是上一步Delaunay生成后的直线。这一步的生成效果如图1所示。
1.3 方向角平分线剖分
以上一步Voronoi图的结果按照每一独立站点包含的小区的方向角平分线来进行分割,得到小区的模拟覆盖区域,这就是现阶段各类软件可达到的小区模拟划分的结果,划分效果如图2所示。
1.4 现有剖分的误差
现有的剖分实际上可以理解为相邻站点采用中垂线进行剖分,但实际现网小区存在着挂高、下倾角、天线类型、海拔高度、发射功率等差异,采用垂直平分线进行剖分肯定和现实情况差异较大。
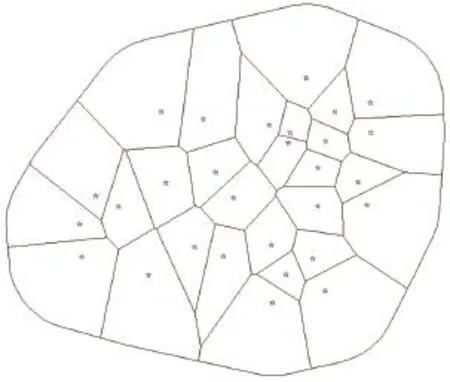
图1 Voronoi图的站点效果
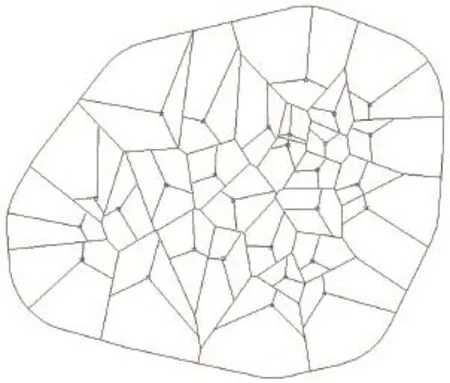
图2 Voronoi图的小区效果
但三角形的三条边的垂直平分线相交于外接圆的圆心,这一特点导致只有通过垂直平分线才能保证区域被完整分割。这也是Voronoi图的基本出发点,如果通过简单的更改剖分的位置点必然导致三角形内部划分混乱。可以说如果还在此基础上进行改良很难得到能够表示小区覆盖区域的模拟剖分多边形。
2 新划分方法的引入
2.1 新方法的整体思路
考虑只使用简单的自由空间传播损耗公式,不考虑地物类型也可以对电平情况进行简单预估,预估的结果用来进行小区区域的划分。考虑到绝大多数区域的邻近小区间的地物类型应该相同,海拔差异不会很明显,使用自由空间传播损耗公式可以得到比较真实的最佳小区划分。
整体思路为:首先按照之前的Voronoi图生成过程使用中垂线的划分方式得到粗略的小区区域划分,接着对站点分布区域生成预定义大小(50×50)的栅格,对小区所属站点周边站点区域范围内的每一栅格点按照自由空间传播损耗公式:LS=32.45+20lgF(MHz)+20lgD(km)进行预测,对每一栅格点只保留最大场强的小区标示,预测电平。随后将同一属性的栅格进行合并,边界进行平滑处理得到小区模拟覆盖区域。
每一栅格点的预估场强= 小区的有效发射功率-(32.45+20lgF(MHz)+20lgD(km))+天线的标称增益+天线水平方向增益+天线垂直方向增益。
以上公式中对于每一栅格点存在变化的有距离D;天线水平方向增益;天线垂直方向增益。其余参数对于特定的小区来说都是常量。
2.2 新方法的大体过程
(1)按照前面已述方法生成小区的Voronoi划分区域,见图3所示。
(2)生成网格,判断A小区的Voronoi相邻区域及自身作为A小区的预测区域,见图4所示。
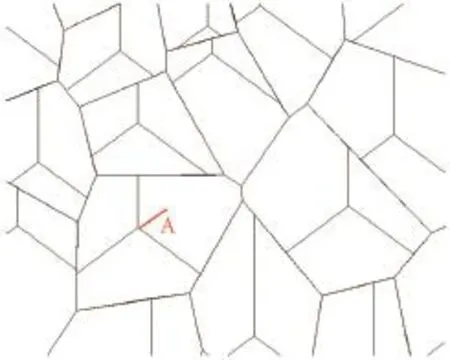
图3 小区的Voronoi划分异
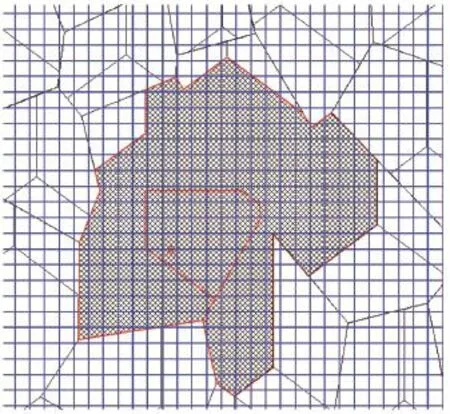
图4 判定小区的预测区域

图5 传统方式和新方法小区划分的对比
(3)读取小区的天线配置及工程参数,对上述区域的每一网格点都进行场强值的计算,场强值=小区的有效发射功率-(32.45+20lgF(MHz)+ 20lgD(km))+天线的标称增益+天线水平方向增益+天线垂直方向增益,将网格属性值(归属小区,场强)进行更改;
(4)对所有室外小区都完成同样3~7步的计算,用最大值替换网格属性;
(5)将同一属性的网格进行合并,并将外围平滑化。
2.3 新方法效果
图5分别是同一区域使用传统方法得到的小区边界划分和新方法划分的对比。
总体比较,从划分效果上新的模拟划分效果更加贴近小区的实际覆盖,在运行效率上同一台电脑上进行比较,对923个小区进行运算,规划软件耗时866s,新算法划分耗时20s。算法刚刚实现还存在优化的可能,优化后运算时间还能有所提升。
3 总结
由上可知采用新的方法可以在不使用三维数字地图的基础上高效地生成非常贴近实际网络覆盖情况的小区多边形,这为很多依据小区多变形划分的应用打好了基础。
