神经网络模糊直接转矩控制在感应电机中的应用研究*

乔维德

（常州市广播电视大学，江苏 常州 213001）

1 引言

感应电机（IM）直接转矩控制（DTC）是一种新型交流调速系统,与传统的感应电机矢量控制系统相比，不仅具有控制直接、计算过程简化的特点，而且在一定程度上克服了矢量控制中控制结构复杂，系统易受电机参数变化和外界因素扰动影响等问题。但直接转矩控制中，由于转矩和磁链调节器采用滞环比较器，不可避免地造成了转矩脉动，而且在感应电机运行一段时间后，电机温度升高，定子电阻的阻值发生变化，使定子磁链的估计精度降低,从而导致电磁转矩出现较大的脉动。此外，逆变器开关状态的选择也会影响转矩脉动的大小与系统的控制性能。因此，为了抑制转矩脉动，有效提高感应电机直接转矩系统的动、静态性能，本文提出基于神经网络和模糊逻辑的感应电机直接转矩控制策略，即利用神经网络构造定子磁链观测器，应用模糊逻辑推理设计逆变器状态开关选择器，从而使感应电机直接转矩控制系统获得较强的鲁棒性和优良的动态性能，对此进行了仿真分析,并利用TMS320F2407A数字信号处理（DSP）芯片进行实验验证。

2 感应电机神经网络模糊直接转矩控制系统

2.1 控制系统结构

图1 感应电机神经模糊直接转矩控制结构

感应电机神经网络模糊直接转矩控制系统结构如图1所示。

图1中，ω*为给定角速度，ω为实际转子角速度为给定电磁转矩，Te为实际电磁转矩为给定定子磁链，ψsα、ψsβ为定子磁链在 α-β坐标中的分量；usα、usβ为电压在 α-β 坐标中的分量；isα、isβ为电流在α-β坐标中的分量；θ为磁链位置角。

利用电压电流检测单元检测感应电机的定子三相电流 iA、iB、iC和电压 uA、uB、uC，通过 3/2 变换成两相值 isα、isβ和 usα、usβ，输入至神经网络定子磁链观测器。通过神经网络模型输出两相磁链ψsα、ψsβ，然后利用转矩模型和磁链模型分别计算电机的转矩、磁链和位置角大小［4］-［6］。计算公式为：

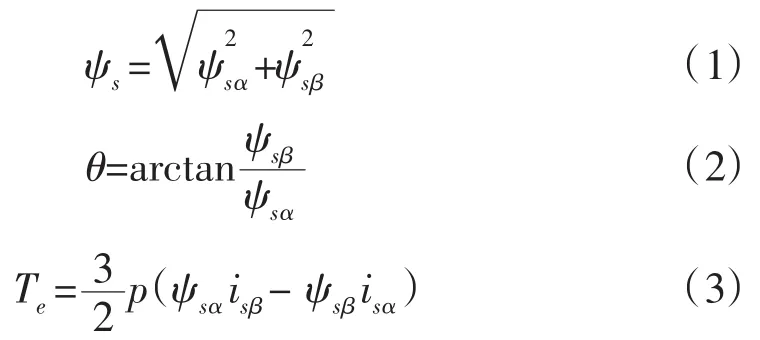
图1中采用模糊控制器取代常规直接转矩控制系统的磁链和转矩控制器。将给定的电机转矩、磁链值和实际计算值Te、ψs相比较得到的转矩误差eT、磁链误差eψ直接用于开关状态的选择，这里引入模糊控制逻辑后，则可以通过区分eT和eψ的大小作出不同决策来优化输出开关状态，并经逆变器控制IM定子的三相电压和电流，使电机能按控制要求输出转矩，最终达到调速的目的。

2.2 神经网络定子磁链观测器的设计

2.2.1 神经网络结构

应用三层前向BP网络设计定子磁链观测器，神经网络结构模型如图2所示。

图2 神经网络结构模型图

第一层为输入层，输入层的各个节点直接与输入变量连接，其节点数取决于输入信号，输入信号共有 5 个，即 S1-S5，分别对应定子电压 usα、usβ，定子电流isα、isβ以及电机角速度ω。

第二层为隐含层，其节点数m是在网络学习过程中根据实际情况而定的，一般可按经验公式m=（输入节点数+输出节点数）1/2+a和神经网络训练过程中的实际输出磁链ψs（由ψsα和ψsβ计算合成）与期望输出磁链ψ*s的误差值来综合考虑设置，其中a为1-10之间的常数，这里m取为6。对于隐含层的第i个节点，设该节点与输入各节点的连接权值为ωij，则其输出为 yi=f（ΣωijSj+θi），其中 i=1，2，…m；j=1,2,…5；f为神经元的非线性作用函数，选取Sigmoid型变换函数，即f（x）=1/（1+e-x），x为神经元的输入值；θi为节点的阈值。

第三层为输出层，输出层有2个单元O1和O2，分别对应ψsα、ψsβ。输出节点与隐含层各节点的连接权重为Tki，节点阈值为θk，则输出节点为：Ok=f（ΣTkiyi+θk）其中 i=1，2，…，m；k=1，2。

2.2.2 神经网络的训练

神经网络的学习训练就是通过训练样本的学习，不断调整输入层到隐含层、隐含层到输出层之间的两组连接权值和阈值，即 ωij、θi、Tki、θk，从而使网络的误差逐步减小直至规定的目标精度。在对神经网络训练时，考虑到粒子群优化（PSO）算法全局寻优能力强和BP算法善于局部搜索的特点，本文采用将两者相结合的方法，即PSO-BP算法［4］。具体训练过程如下。

（1）随机初始化神经网络的各个连接权值ωij、Tki和阈值θi、θk，并对应为一群粒子的相应位置xi和速度vi。本文取粒子群体规模M=80，连接权值ωij、Tki和阈值 θi、θk的随机取值范围分别选取为［-1，+1］和［-10，+10］。

（2）给定惯性权重ω，加速因子（或学习因子）C1、C2，约束因子α，初始化第i个粒子目前为止搜索到的最优位置（与下面的最好适应度值对应）为Pi（i=1，2，…M）；群体所有粒子目前为止搜索到的全局最优位置记为Pg。神经网络输入层输入信号,对网络进行前向计算，并根据适应度函数（均方误差）公式f=λ|Ok-Qk|的计算结果来评价每个粒子的适应度。其中Ok为网络实际输出值，即定子磁链ψs；Qk为理想期望输出磁链值，λ为正常数。

（3）对每个粒子，将它的适应度和它经历过的最好位置Pi时的适应度相比较，如果比Pi时的好，则将其作为当前最好位置，将它的适应值和全局所经历最好位置Pg时的适应度作比较，若较Pg时的适应度好，则重新设置Pg的索引号，并记录Pg的值，采用公式（4）、（5）对粒子位置 xi和速度 vi进行调整［8］-［10］。

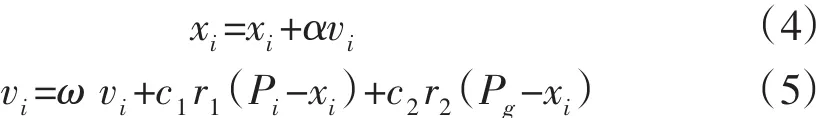
式中：i=1，2，…，M；惯性权重ω指示粒子保持运动惯性大小；加速因子C1、C2用来分别调节向全局最优粒子和个体最优粒子方向飞行的最大步长，通常取大于零的常数；r1、r2为介于［0，1］区间的随机数，约束因子α的作用是控制速度的权重。本文取 α=0.8，ω=0.5，C1=C2=2。

（4）粒子群在解空间进行搜索，若迭代次数小于最大迭代次数NCmax（本文取500）时，则转入步骤3），否则转至步骤 5）。

（5）在粒子群算法全局寻优的基础上，运行小步长反向传播BP算法，进行局部细致搜索，直至达到规定要求的收敛精度（0.001），输出神经网络的最终权值和阈值，结束网络训练。

3 模糊开关状态控制器的设计

在通常的直接转矩控制系统中，磁链误差eψ和转矩误差eT被直接用于逆变器开关状态的选择，无法区分eψ和eT的等级，不利于解决直接转矩控制系统中存在的电机或负载参数变化等不精确和不确定信息的控制问题。本文引入模糊控制之后，通过区分eψ和eT的大小来优化逆变器开关状态的选择,从而达到改善系统性能的目的。

3.1 模糊变量

在模糊控制器中，eψ和eT分别被模糊化为模糊变量 Eψ和 ET，Eψ在论域（-0.01，0.01）上定义 3 个模糊子集，语言值取为｛N（负），Z（零），P（正）｝。ET在论域（-2，2）上定义5个模糊子集，语言值取为｛NL（负大），NS（负小），Z（零），PS（正小），PL（正大）｝。为增强系统鲁棒性，以上两个论域中，均采用对称的全交叠的三角形隶属度函数，如图3、4所示。

图3 Eψ的隶属度函数

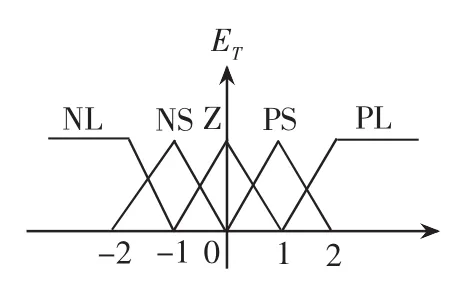
图4 ET的隶属度函数

另一个输入量—定子磁链位置角θ在论域0-2π 划分为 12个模糊子集（θ1-θ12），其变量隶属度函数分布如图5所示。

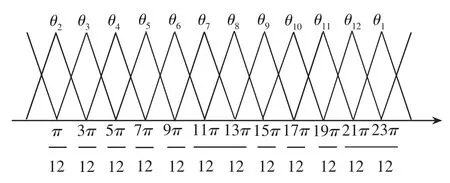
图5 θ的隶属度函数

模糊控制器的输出变量对应逆变器的8个开关状态，即 V0-V7，V0（000）和 V7（111）为两个零状态，逆变器输出电压为零，所以逆变器有效开关状态为6个 ，即 V1（011）、V2（001）、V3（101）、V4（100）、V5（110）、V6（010）。如输出 V3（101）表示逆变器的三相电压开关状态 SA=1，SB=0，SC=1（1为开通，0为关断）。

3.2 模糊规则及模糊推理［5］

根据直接转矩控制原理和控制经验，可确定180条控制规则，模糊控制器的每一条控制规则均使用 Eψ、ET、θ、V 来描述，其中第 i条规则为：

模糊推理采用Mamdani规则，输出开关量Vi取最大的隶属度对应的输出量作为逆变器的开关输出。用公式表示为：

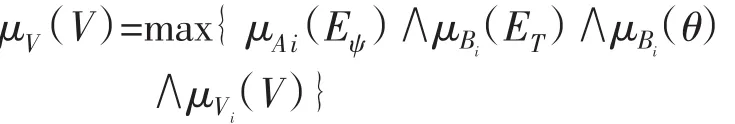
式中：i=1，2…180；μA、μB、μC分别为 Ai、Bi、θi的隶属度；μV为输出V的隶属度。

4 仿真研究

图6 常规DTC仿真响应曲线

基于上述控制策略，在Matlab/Simulink环境下建立感应电机直接转矩控制系统模型，分别对常规DTC以及神经网络模糊DTC进行了仿真。仿真用感应电机主要参数如下：额定功率Pn=2.2kW，额定电压Un=220V，额定电流In=5A，额定转速nn=1500r/min，定子电阻Rs=2.5Ω，转子电阻Rr=2.76Ω，定子电感Ls=0.06535H，转子电感Lr=0.08014H，定转子互感Lm=0.06265H，转子极对数np=3，转动惯量J=0.00158kg·m2。如图6和图7所示分别为常规DTC和神经网络模糊DTC的转矩、磁链、转速的响应曲线。从图 6（a）、图 7（a）明显得出，基于神经网络模糊控制下的系统转矩响应较常规直接转矩控制响应平稳，速度快，超调和脉动都很小。由图 7（b）和图 6（b）比较可以看出，在神经网络模糊直接转矩控制下转速从0上升到60rad/s只需要0.01s，从 60rad/s跳变到 120rad/s也不足 0.01s（约0.0085s），而且转速响应较传统DTC平稳、脉动小。图 6（c）和图 7（c）表明，神经网络模糊直接转矩控制下的磁链瞬时幅值的脉动显著减小。由此可见，在传统DTC基础上引入神经网络模糊控制后，控制系统转速和转矩响应快速、平稳，转矩及磁链响应脉动明显减小，从而使系统运行稳定，获得了比常规DTC更优异的动、静态性能。

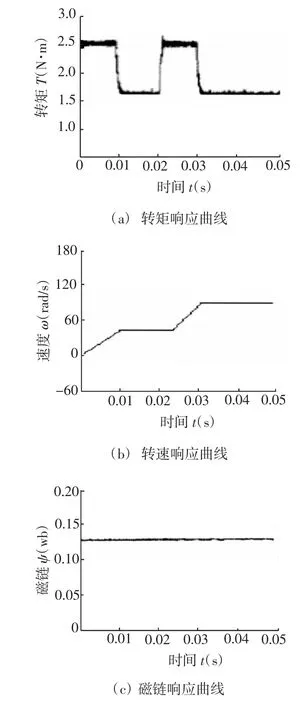
图7 基于神经网络模糊DTC仿真响应曲线

5 实验验证

实验电路中，采用TMS320LF2407A数字信号处理器（DSP）完成神经网络模糊直接转矩控制的部分实验。实验控制系统结构如图8所示。基于DSP的核心控制电路主要负责控制算法以及协调控制周边电路，DSP获得检测到的定子电流及电压信号后，完成神经网络、模糊控制算法和直接转矩控制的计算 (包括三相/二相变换、磁链和转矩计算、逆变器开关状态的控制等)，最后得到6路PWM控制信号，经驱动隔离后控制作为逆变器的功率模块IPM。采用CHB5-P型霍尔电流传感器来检测电流，采用OVW2-2048-2MD型旋转编码器进行转速检测。外部扩展电路主要完成电压、电流和速度信号的检测、数据显示以及DSP与上位机的通信等功能，并对逆变器IPM发出的各种故障信号进行综合处理形成总的故障信号送入TMS320F2407A的故障中断入口，用于系统保护和故障显示。PC机采用VB编写通信界面，主要负责转速和磁链的给定以及调速系统故障显示等功能。

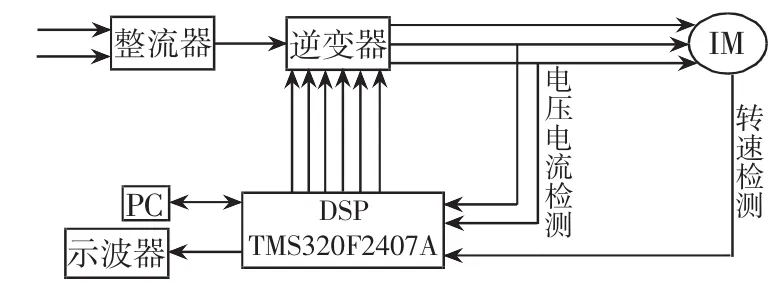
图8 系统结构框图

本实验系统软件的开发采用模块式结构，包括主程序和中断服务程序两部分。主程序完成DSP的初始化、参数设定和故障诊断。要实现的采样周期的定时、神经网络、模糊控制、直接转矩控制等系统的主要功能和控制算法由DSP的定时器1下溢中断服务程序来完成相应的感应电机控制策略。

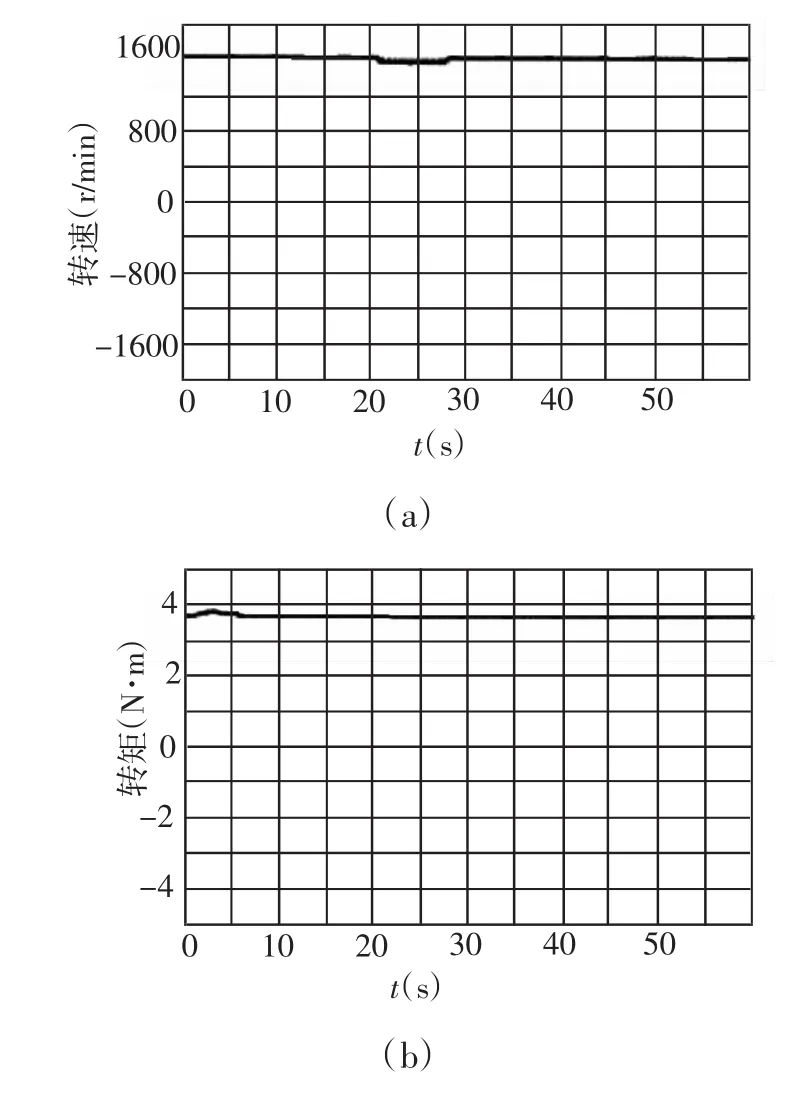
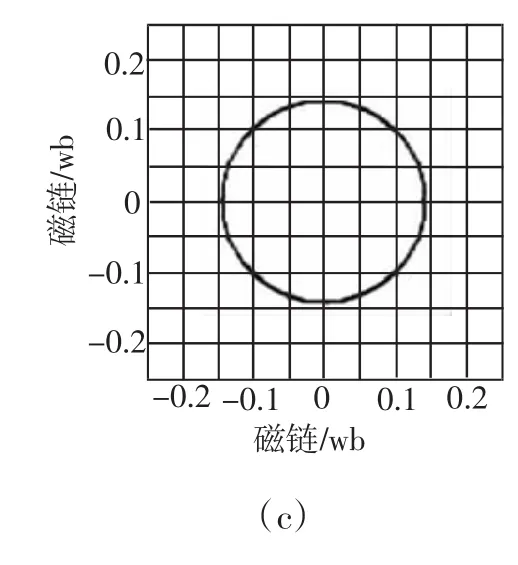
图9 转速响应曲线、电磁转矩波形及定子磁链轨迹

图9（a）显示本系统在跟踪恒定转速1500 r/min稳定运行并在t=20-30s突加2 N·m负载时的转速响应曲线；图9（b）、图9(c)分别为额定运行的电磁转矩波形和定子磁链轨迹。从图中可以明显看出，经过系统控制的磁链波形接近圆形，系统响应速度快，有效抑制转速脉动、转矩脉动和磁链脉动，能得到与仿真基本相似的实验结果。

6 结束语

感应电机直接转矩控制系统是一个具有深刻研究意义的的课题。本文在常规直接转矩控制的基础上，提出了基于神经网络和模糊逻辑的直接转矩控制方法。仿真分析与实验结果表明，该方法的使用有效地降低了系统的转矩脉动、磁链脉动等，系统具有优良的速度、转矩响应特性以及较强的鲁棒性和控制性能，从而为感应电机直接转矩控制系统的研究提供一种新的思路和方法，具有良好的应用前景。

［1］周华伟,刘国涛.感应电机直接转矩控制系统的研制［J］.微特电机,2007,35（5）:36-38.

［2］白华煜,刘 军,楚小刚.基于模糊控制感应电机直接转矩控制研究［J］.电气传动,2005,35（5）:6-9.

［3］乔维德.基于改进PSO-BP神经网络的短期电力负荷预测研究［J］.继电器,2007,35（17）:17-21.

［4］乔维德.遗传模糊神经网络在交流伺服系统中的应用［J］.江苏电器,2007,27（2）:29-31.