一种基于改进的模糊Smith预估器冷轧AGC控制系统

安连祥，马华民，刘新艳，刘永刚

（河北工业大学电气学院，天津300130）

1 前言

冷轧AGC 是带钢生产线上应用最广泛的厚度控制系统，其控制效果直接影响到带钢的最终质量。一方面，AGC 控制系统具有时滞、时变、大惯性、非线性等特征。另一方面，在实际应用中还要求具有超调量小、响应速度快以及抗干扰性强的特性。典型的AGC 控制系统可以简化为一个二阶对象和一个纯滞后环节，而时滞的存在会对控制系统的性能产生不利影响。用常规的PID 控制方法难以取得较好的控制效果，甚至出现不稳定现象。最常用的方法是采用Smith 预估器解决时滞的补偿问题，但由于其对模型的误差十分敏感，鲁棒性较差，因而限制了它在工业控制中的广泛应用。

近年来，由于模糊控制具有不需要精确数学模型，对参数变化不敏感，鲁棒性强等特点，被广泛应用于工业控制领域，故将Smith 预估器和模糊控制结合起来组成模糊Smith 控制系统来改善控制效果，但它并没有从本质上克服时滞给系统性能带来的影响，当模型误差较大时，控制效果仍很差，鲁棒性不强。鉴于此，本文提出一种改进的模糊Smith 预估控制系统，可以克服以上缺点，明显提高控制性能。

2 模糊Smith 预估控制器

常规Smith 预估控制器的结构如图1所示，图中G（s）e-τs为被控对象，当Smith 预估器的Gm（s）=G（s），τm=τ 时，模型无误差。不考虑模糊控制器，此时系统的闭环传递函数为：

图1 模糊Smith 控制系统结构图

可见此时系统的特征方程中已不含时滞环节，消除了纯时滞对系统品质的影响。相当于把G（s）作为控制对象，闭环传递函数分子上的时滞环节只说明输出比设定延时τ 时间。

虽然模糊控制器有许多优点，但它仍不能单独代替Smith 预估控制方案中的PID 调节器。因为模糊控制器的输出是根据偏差和偏差的变化进行推理而得到的，本质上属于PD 控制，无法消除系统的稳态误差。而且模糊控制器的控制效果不仅与控制规则有关，还与量化因子和比例因子的选择有关，量化因子和比例因子对模糊控制器的控制性能影响极大，而要得到一组合适的参数并不容易。同时，虽然模糊控制器对模型参数变化不敏感，但当Smith 预估器的模型与对象模型相差较大时，模糊控制器亦显得无能为力。本文提出的方法分别对模糊控制器和Smith 预估器进行改进，仿真结果表明，该方法可以显著提高控制性能。

3 改进的模糊Smith 预估控制器

3.1 模糊控制器的改进

改进后的模糊Smith 预估控制器的结构如图2所示。控制器根据厚度偏差e 的大小划分为三个不同的控制区域，在各个不同的区域中采取不同的操作，具体形式如下：

图2 改进后的模糊Smith 控制系统结构图

3.2 Smith 预估器的改进

虽然模糊控制器能够克服模型失配带来的不良影响，但只有在模型失配不大时才有一定程度的效果，随着模型误差的增大，其控制效果明显下降。因为原Smith 预估器反馈通道信号未考虑到过去的或历史的偏差数据对预估值的影响，所以当模型失配时，原Smith 控制结构存在不合理性。为克服这一缺点，新的控制方案考虑到过去偏差的影响，在主反馈通道中引入一个惯性环节1/（tf+1），对偏差进行了低通滤波处理，其中tf为滤波时间常数。

由图2可见，当模型无误差时，主反馈通道为零，与普通Smith 预估器没有区别。只有当模型失配时，即时间常数、时滞时间、放大倍数其中之一存在误差时，主反馈通道才不等于零。仿真研究表明，如果模型失配是由放大倍数引起的，则惯性环节的引入不但不能改善控制效果，反而会使控制性能下降,当放大倍数误差较大时，模糊控制器已经难以克服放大倍数的不良影响；对于其他参数引起的模型失配，惯性环节的引入对系统性能有较大的改善。为此，本文引入一个自适应机构，根据模型失配的原因对系统进行调节。其基本原理为：把对象输出值Y 和模型输出值Ym相除，若模型失配仅由放大倍数引起，则Y/Ym等于一个常数，其导数为零，据此利用自适应机构将模型Gm（s）乘以Y/Ym的值，使模型相配。若Y/Ym的值不等于常数，则模型失配是由放大倍数以外的其他参数引起，自适应机构不对系统起作用，惯性环节1/（tf+1）照常工作，从而改善控制性能。可令滤波时间常数tf等于模型时滞常数τm，tf取值过小则滤波效果不明显，控制性能与引进滤波器前改善不大；tf取值过大虽然有利于消除振荡，使响应曲线平滑，但这增大了系统的调节时间，不利于对象输出快速跟踪给定值。仿真结果表明，对参数波动较大的大时滞系统，该方法改善了系统控制特性，使系统具有较强的鲁棒性。

4 系统仿真

为验证改进后的模糊Smith 控制器在冷轧AGC 控制系统中的优越性，以下用该方法和普通模糊Smith 预估控制器对典型的AGC 控制系统进行了仿真。设其模型如式（2），模糊控制规则如表1所示。厚度给定为1mm，取A1=0.05mm、A2=0.4mm，开关控制的正值和负值分别为2 和-2。模糊控制器输入e，ec 的论域为［-6，6］，量化因子为6；输出u 的论域为［-10，10］，比例因子为0.5。PID 控制器的比例、积分、微分系数分别为5、0.6 和4。利用Simulink 进行仿真，固定步长为0.1s。

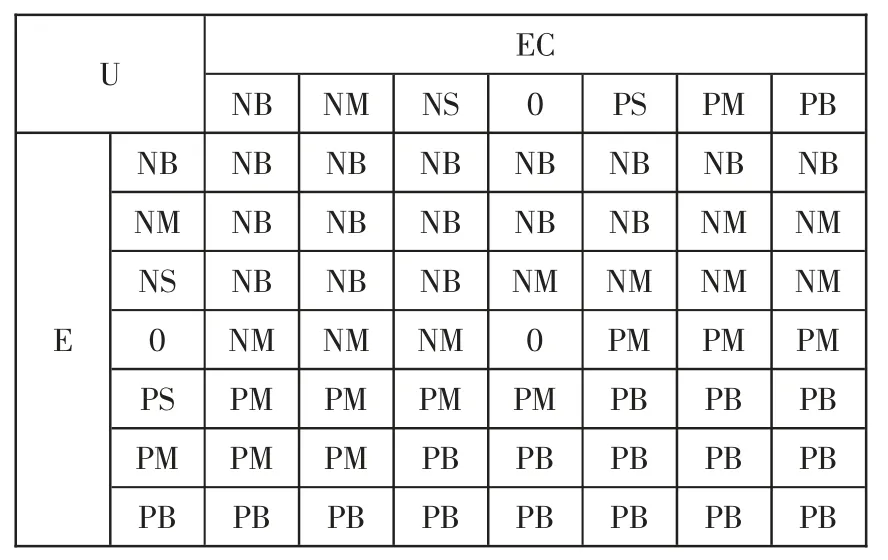
表1 模糊控制规则表

4.1 放大倍数引起的模型失配

自适应机构能够根据Y/Ym导数的值对模型失配原因进行判断。当模型失配由放大倍数引起时，自适应机构将Smith 模型乘以Y/Ym的值，使模型相配，相当于仅仅是被控对象的放大倍数改变了。当被控对象的放大倍数增大50%和减小50%，即当K=1 和K=3 时，仿真结果如图3（a）、3（b）所示，以下各图中data1 均为改进后的模糊Smith 预估器仿真曲线，data2 均为常规模糊Smith 预估器仿真曲线。

4.2 时间常数和滞后时间引起的模型失配

当模型失配是由放大倍数以外的因素引起时，主反馈通道的惯性环节起作用，利用过去的偏差对预估模型的反馈进行补偿。当模型失配由时间常数A 引起，A 增大50%和减小50%，即A=4.5 和A=1.5 时，仿真结果如图4（a）、4（b）所示。当模型失配由滞后时间τ 引起，τ 增大50%和减小50%，即τ=7.5 和τ=2.5 时，仿真结果如图5（a）、5（b）所示。

图3 K 改变时的仿真曲线

图4 A 改变时的仿真曲线

图5 τ 改变时的仿真曲线

5 结论

通过以上仿真研究可知,本文提出的改进的模糊Smith 预估控制方法,充分发挥了模糊控制器和Smith 预估器的优点,不仅能够抑制时滞带来的不良影响，而且对参数变化具有较强的适应能力，同时消除了常规模糊控制器由于缺乏积分作用造成的稳态误差，提高了系统控制精度，简化了模糊控制器的设计，增强了系统的鲁棒性和抗干扰能力，对系统的动、静态性能有很大的改善，为工业生产的大时滞过程提供了一种行之有效的控制方法。

［1］陶永华,尹怡欣等.新型PID 控制及其应用［M］.北京：机械工业出版社,1998.

［2］韩立强,李志宏.一种改进结构的Smith 预估器及在轧机AGC 中的应用［J］.河北大学学报，自然科学版2004,24（2）:130-133.

［3］杜安静，朱学峰.一类改进的模糊Smith 预估控制系统［J］.模糊系统与数学,2001,15（1）:97-102.