节能减排背景下的火电AGC机组组合优化研究

马一凯 雷霞 柏小丽 程政 孔祥清

（西华大学电气信息学院，成都 610039）

1 引言

节能减排发电调度[1]，要求在电力系统安全稳定运行和连续供电的前提下，最大限度地减少能源、资源消耗和污染物排放。在安排机组出力时，只考虑机组煤耗虽能达到节能降耗目的，但不能体现市场主体意愿；如果只考虑市场主体意愿，而忽视机组煤耗排放等因素，节能降耗将难以充分实现[2]。

经济和环保是两个互有矛盾性的优化目标，在现有的优化调度方法中多为单目标优化，而将二者有效衔接的实际模型较少。文献[3]探讨了无节能约束、节能约束、能耗最低等三种电力市场的解决方案，提出节能约束下的电力市场模式、基于年度、月度中长期电力市场，建立了市场竞价模型，提出了竞价算法，但没有分析减少污染排放对电力市场的影响；文献[4]提出了一种以能耗与污染物排放最少为目标的发电侧节能减排新模式。通过可变成本排序和污染物排放量排序确定机组上网电量，以达到节能减排的社会目标，但是没有考虑针对各个机组特点的约束条件；文献[5]详细论述了实行节能发电调度对推动电力行业低碳化发展的巨大效益，建立了适应不同电力调度模式的排放计算模型，并对相应的CO2排放轨迹做出了分析，提出了以机组年发电小时数差异为控制要素的电量分配方法，但并没有结合机组组合给出具体的分析结果。

本文提出的机组组合优化模型是在满足经济调度目标前提下，加入节能减排新要求的目标函数，通过引入排放成本系数和调度权重因子，将两目标优化函数转变为单目标优函数，通过动态规划法的前向算法来解模型，以达到经济、节能、环保的优化调度目的。

2 模型的建立

传统的机组组合模式[6]只以报价高低决定机组上网电量的多少，以发电成本最小为优化目标，未考虑机组能耗和排放问题；节能减排模式以能耗最小、排放最少为优化目标，将发电能耗和环境保护相结合。两种模式寻优目标不同，本文正是在传统机组组合模型的基础上，提出经济性兼顾节能减排的双目标AGC机组优化调度模型。

2.1 目标函数

（1）经济性目标

式中，F为发电费用成本函数，单位为元；T表示优化时段数，I表示待调度机组数目；Ci为发电费用函数，ui(t)=1时表示开机，ui(t)=0时表示机组关机，pi(t)为机组i在时段t的有功功率；Si为开机费用函数，xi(t)是以该时段前机组i最后一次开机的时段为时间起点，中间机组没有停机，这整个过程内的时段就为累计开机时间，其值为正；机组的连续累计停机时间和机组连续累计开机时间类似，这时xi(t)取负值。

（2）节能减排目标

式中，f为污染气体排放函数，单位为m3；ai、bi、ci为机组i的排放特性参数。

2.2 约束条件

（1）系统功率平衡：t∈{1⋅⋅⋅T},i∈{1⋅⋅⋅I}

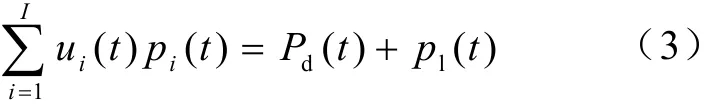
式中，pi(t) 为机组i的发电功率；pd(t)为系统网损；pl(t)为系统负荷。

（2）系统旋转备用约束：t∈{1⋅⋅⋅T},i∈{1⋅⋅⋅I}

式中，pr(t)为系统t时段的总备用要求。

（3）机组出力约束：t∈{1⋅⋅⋅T},i∈{1⋅⋅⋅I}

式中，Pi,min，Pi,max为机组i的最小、最大发电功率限额。

（4）最小开、停机时间约束：t∈{1⋅⋅⋅T},i∈{1⋅⋅⋅I}

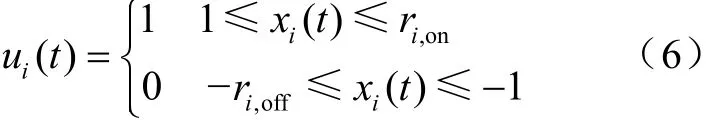
式中，ri,on、ri,off分别为机组i的最小开、停机时间。

（5）机组爬坡速率约束：t∈{1⋅⋅⋅T},i∈{1⋅⋅⋅I}

式中，Pi,up为机组i时段爬坡功率的最大值。

3 解模型

机组组合优化是一个高维数、非凸、离散、非线性的混合整数优化问题。众多学者提出了各种解决方法。文献[7]分类综述了从 60年代起该问题的主要解法，比较了启发式方法，动态规划法，混合整数规划法，拉格朗日松弛法，遗传算法等优化方法的优缺点，并提出了尚待研究的问题。

动态规划法把 UC问题看成按时间分段的多步决策过程，即把多时段问题分解成相互关联的一系列单时段问题，在整个周期范围内确定机组起停过程，以寻找各时段内机组状态的最优路径。本文正是应用动态规划法的前向算法对所建机组组合模型进行求解。

动态规划法[8-9]分为前向算法和后向算法。后向法的解决方法是从最后时段开始，直至倒推到初始时段，因此当处理的数据量较大、阶段数较多时，后向算法并不能包含许多实际情况，例如：如果机组的起动费用是它离线时间的函数，那么前向算法就更加适合，因为每个阶段的机组先前的历史数据可以计算得到。使用前向法，还存在着其它一些实际原因，即有利于起始条件具体化，只要计算存储空间足够，计算就一直能够及时前向进行。

本文通过引入排放成本系数iβ，即机组i在单位排放量下消耗的标准煤的费用，对其定义说明如下

式中，mi(t)为t时间段内机组i的燃煤费用，fi(t)为第t时段内机组i的废气排放量，单位为m3，本文中的βi由各机组本身的特性决定。于是将机组发电成本和机组排放最小的多目标问题转化为如下单目标问题：

基于动态规划前向算法的基本方程[10]和本文所建数学模型，计算时段 t内组合 k的最小费用的递推公式由下式给出：

式中，（t,k）表示t时段的第k种机组组合 k∈{1⋅⋅⋅2I}，Qmin(t, k)为状态（t,k）下的最小总费用，(1−λ)C(t, k )为状态（t,k）时的经济机组的运行费用，S(t−1,m|t, k )表示从前一状态(t−1,m )到后一状态（t,k）的机组开停机转换费用，λ G(t, k)为状态（t,k）下减排机组的运行费用。

算法步骤概括如下：

第一步：从时段 t=1开始，枚举所有满足约束条件的K个可行组合，在这点上，经济调度问题将执行计算阶段t时每个可行的组合费用

第二步：对于阶段t+1，枚举所有满足约束条件的J个可行组合，计算此时新的负荷水平下的每个可行的组合费用

第三步：计算所有从阶段(t, k)到阶段(t+1,j)可行的转换，如果该机组满足约束条件，那么就要计算开机费用，如果同时有多台机组开机，则

n是从阶段(t, k)到阶段(t+1,j)开机的机组数目。

第四步：利用递推公式（10）实现从阶段 t到阶段t+l的转换的总费用，即前面所有时段的累计费用和当前状态的最小费用之和：

第五步：保存最小值，同时保存此最小值对应的路径。

第六步：进行下一阶段，重复步骤二至五。

第七步：当到达最后阶段，计算最小总费用，并回溯找到最优路径。

上述步骤的流程如图1所示。

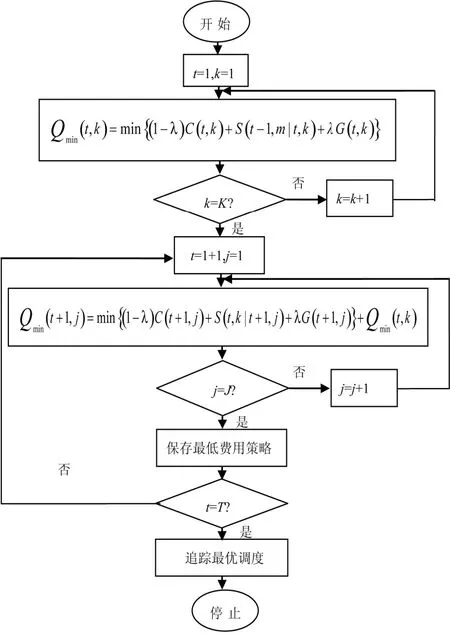
图1 算法流程图

4 算例仿真

下面对6机组8时段（每时段取1小时）的电力系统进行算例仿真。系统旋转备用取系统总负荷的8%，火电机组详细数据和系统负荷参见文献[11，12]。λ的取值则由系统调度员根据上级下达的减排指标确定，不同的减排指标下对应的λ值的大小不同，可以通过变步长迭代法来确定[13]，本文实现的是按系统减排10%调度AGC机组，这时λ取0.2。采用 Mat1ab7.0实现相应的算法计算程序，应用动态规划法的前向算法分别对目标函数（1）、（2）、（9）式进行计算。所得结果如表1所示。

对比综合优化和经济优化可以看出，排放降低9.96%时的最小调度费用为137564.4元。表2所示的是不同优化调度方式下的开停机计划。

表1 三种不同目标函数的优化结果

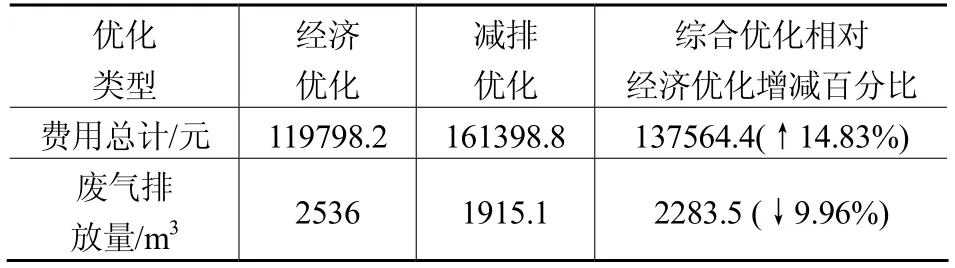
表2 三种不同优化目标的机组开停计划

5 结论

在节能减排背景下，从经济性和环境保护角度出发，针对火电AGC机组提出了发电费用最小和污染气体排放最小的多目标优化调度模型，由于AGC机组运行的经济型和节能减排是相互矛盾的优化目标，要解决这个问题，必须找到合理的方法[14-15]。本文所建模型处于一种折中的考虑，即在达到相应的减排目标的前提下实现机组的调度总费用最小，算例仿真表明，该模型能较好兼顾火电AGC机组的运行成本和环境保护的利益要求，适应了可持续发展战略的要求。

[1]中华人民共和国中央人民政府门户网站.国务院办公厅关于转发发展改革委等部门节能发电调度办法(试行)的通知(国办发[2007]53 号)[EB/ OL].http∶//www.gov.cn/zwgk/2007-08/07/content_708486.htm, 2007-08-07.

[2]胥传普,杨立兵,刘福斌.关于节能降耗与电力市场联合实施方案的探讨[J].电力系统自动化.2007, 31(23)∶ 99-103.

[3]耿建,高宗和,杨争林,等.节能电力市场设计初探[J].电力系统自动化,2007,31(19)∶18-21.

[4]苗增强,谢宇翔,姚建刚,等.兼顾能耗与排放的发电侧节能减排调度新模式[J].电力系统自动化,2009,33(24)∶16-20.

[5]陈启鑫,周天睿,康重庆.节能发电调度的低碳化效益评估模型及其应用[J].电力系统自动化,2009, 33(16)∶24-29.

[6]刘维烈.电力系统调频与自动发电控制[M].北京∶中国电力出版社,2006∶116-126.

[7]陈皓勇,王锡凡.机组组合问题的优化方法综述[J].电力系统自动化,1999,23(4,5)∶51-56.

[8]Momoh.J.A,Yi Zhang. Unit commitment using adaptive dynamic programming[J]. IEEE.Intelligent Systems Application to Power Systems, Proceedings of the 13th International Conference on. 2005∶523-526.

[9]J.Si,A.G.Barto,W.B.Powell,andD.C.Wunsch. Handbook of Learning and Approximate Dynamic Programming[J].IEEE Press Series on Computational Intelligence.2004∶561-596.

[10]胡良剑,丁晓东,孙晓君.数学实验-使用 Matlab[M].上海∶上海科学技术出版社.2001∶180-192.

[11]Basu M An.lnteractive fuzzy satisfying method based on evolutionary programming technique for multi objective short-tem Hydro them al scheduling[J].Electric Power Systems Research, 2004,69(2-3)∶ 277-285.

[12]Ma Haili, Shahidehpour S M,M arw ali M K C.Transmission Constrained Unit Commitment Based on Benders Decomposition[A].Proceedings of the American Control Conference[C].A lbuquergue,New Mexico,1997∶ 2263-2267.

[13]徐致远,罗先觉,牛涛.综合考虑电力市场与节能调度的火电机组组合方案 [J].电力系统自动化,2009,33(22)∶14-17.

[14]袁晓辉,袁艳斌,等.电力系统中机组组合的现代智能优化方法综述[J].电力自动化设备,2003,23(2)∶73-78.

[15]李学斌.机组负荷分配的多目标优化和多属性决策[J].电力系统及其自动化学报,2010,22(1)∶142-145.