炸药爆轰驱动水的初期过程*
2010-06-21龙新平蒋治海黄毅民
龙新平,韩 勇,蒋治海,黄 辉,黄毅民,洪 滔
(1.中国工程物理研究院,四川 绵阳 621900;
2.中国工程物理研究院化工材料研究所,四川绵阳 621900;
3.北京应用物理与计算数学研究所,北京 100088)
1 引 言
液体在炸药爆轰的驱动下变形、破碎及雾化过程是流体动力学具有广泛应用背景的领域。在民用建筑拆除方面,在爆破拆除的同时,通过炸药爆炸抛撒形成一定空间的气溶胶云团,达到抑制粉尘的目的[1]。在军事应用中,云爆武器是典型的应用范例,原理是在战斗部里装填燃料,作用时通过爆炸抛撒将燃料分散在空气中形成可爆炸性的燃料-空气气溶胶云团,在一定条件下引爆,气溶胶云团发生爆炸,产生高温高压,从而对爆炸覆盖区域及以外一定距离的物体造成不同程度的破坏[2-4]。这需要对炸药爆轰驱动液体力学过程的深入了解。
液体爆炸抛撒主要包括以下几个过程[5-8]:首先是早期的驱动阶段,从爆炸产物冲击波在液体介质中的传播及其对液体介质的作用,到流体团块的冲出;其次是近场流体团块或由流体团块形成连贯的流体环的失稳和破碎、整个流体界面形成湍流混合,到流体团块破碎成液滴颗粒;然后是远场液滴颗粒与气流的混合过程,在此过程中液滴颗粒之间发生碰撞、二次破碎、聚合、凝并、汽化或蒸发等,以及颗粒、颗粒群与湍流气流的相互作用现象,最终形成气溶胶云团。针对液体爆炸抛撒过程已进行了大量的工程及基础研究工作,但对炸药爆轰产物驱动液体的初期过程少有文献报道。通过对爆轰产物驱动液体内界面的初期过程进行实验和数值模拟研究,能够获得液体内界面膨胀过程的物理特性和变化规律、液体中冲击波的传播规律,为爆炸抛撒液体外界面的运动规律和失稳过程、液体初级破碎形成液滴的研究提供指导,并为后期液体抛撒过程的数值模型和模拟特性参数的选择奠定基础。因此,对爆轰产物驱动液体内界面的初期过程进行实验和数值模拟研究显得非常重要。
本文中,借助于高速分幅相机FJZ-250,利用阴影照相技术研究炸药爆轰产物驱动液体——水的初期过程,并利用LS-DYNA程序对实验进行数值模拟。
2 实验介绍及结果分析
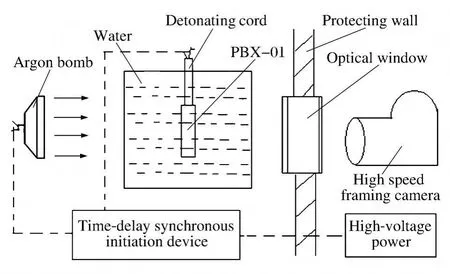
图1 实验测试系统示意图Fig.1 Sketch of experimental arrangement
实验测试系统如图1所示,其中水置于边长为300 mm的正方体玻璃容器内,PBX-01炸药尺寸为∅10 mm×30 mm,炸药及氩气弹均由延时同步起爆装置控制起爆时间。采用阴影照相技术记录炸药爆轰产物驱动水介质界面的运动轨迹。转镜式高速分幅相机的摄影频率为 0.5 μs-1。

图2 炸药爆轰产物驱动水介质不同时刻照片Fig.2 Photos of water expansion driven by detonation product at different times
由图2,当t=0时,爆轰波在铅导爆索中传播,即将进入PBX-01炸药,可清晰地分辨出冲击波在水中的迹线;当t=4 μs时,爆轰波在 PBX-01炸药中传播,未反应炸药阴影保持原来形态,已反应炸药爆轰产物则在水中膨胀形成鼓包,水中冲击波迹线进一步扩大。当t=8 μs时,PBX-01炸药已全部变为爆轰产物,根据PBX-01药柱的长度和爆速,也可得出此时炸药已完成爆炸,这与观察到的实验现象一致,这时水中的冲击波迹线与爆轰产物的形态较为相似。当t=12,16,20,24,28 μs时 ,由 PBX-01炸药爆轰产物在水中的膨胀,以及水中的冲击波迹线发展过程,通过每幅图中PBX-01炸药柱的初始静止像,可精确确定不同时刻炸药爆轰产物的膨胀位置,如图3所示。此外,由图2,冲击波迹线的轮廓由圆锥状较快地演变为类似球形,后期与炸药爆轰产物的形态基本无关,这也可以通过后面不同时刻冲击波迹线示意图形象地表示。实验过程中,爆轰产物和水介质2种不相混的流体之间交界面的不稳定性主要是Rayleigh-Taylor不稳定性,在实验观察的时间范围内(约40 μs),爆轰产物与水介质的接触面轨迹光滑,没有尖钉出现,说明界面没有发生明显的失稳现象。

图3 不同时刻炸药爆轰产物形态示意图Fig.3 Detonation products shapes at different times
3 数值模拟
采用有限元LS-DYNA程序对PBX-01炸药爆轰产物驱动水介质内界面的初期发展过程进行了数值模拟。计算模型中,由于炸药产物和水均有大变形发生,采用多物质ALE单元描述,玻璃属于比较脆的固体材料,在变形过程中有可能破碎,采用LAGRANGE单元描述,并采用流固耦合方法使流体与固体之间发生相互作用。模型初始网格如图4所示,模型中加入了轴对称约束,忽略了铅导爆索,直接采用PBX-01炸药上端面中心点起爆方式。节点44 410为炸药柱一半高度位置处与水接触的一点,节点44 389为炸药底部端面中心点。

图4 计算模型Fig.4 A lattice model for numerical simulation
PBX-01炸药采用高能炸药燃烧模型,爆轰产物状态方程为JWL形式

参数采用VLW热力学程序计算获得[9],密度ρ=1.86 g/cm3,爆压P=37.0 GPa,爆速U=8.8 km/s,A=304.30 GPa,B=11.05 GPa,R1=3.5,R2=1.14,w=0.50,E0=0.012 7。
水采用Gruneisen状态方程[10]
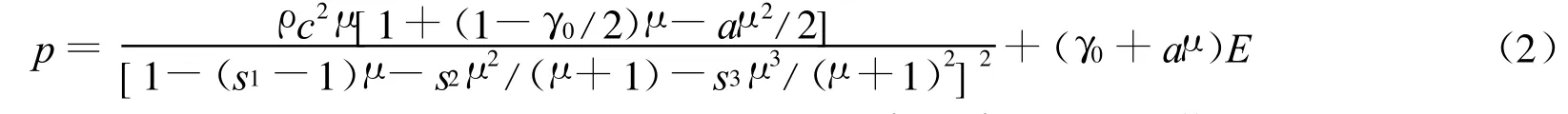
式中:c=1.46 km/s,s1=2.24,s2=-0.278 s/km,s3=0.033 6 s2/km2,γ0=0.5[11]。玻璃采用理想弹塑性材料,ρ0=2.3 g/cm3,剪切模量为4 GPa,屈服强度为0.12 GPa[12]。
图5为12 μs后冲击波阵面示意图。由图可见,冲击波阵面的实验结果与模拟结果基本一致。

图5 冲击波阵面Fig.5 Front of shock wave
沿径向距节点44 410分别为0、10、20、30、40和50 mm等单元的数值模拟压力历程如图6所示,各单元的峰值压力分别为3.01、1.27、0.72、0.43、0.29和0.20 GPa。根据J.M.Walsh等[13]估算温度的方法,在压力为3 GPa时,水的温度约342 K。由于水在常压条件下的相变温度为373 K,根据文献[14]可知,水在2.7 MPa条件下的相变温度为500 K。随着压力的升高,水的相变汽化温度将增加,在本文中的峰值压力下,水的相变温度将远高于342 K,图2中未发现与水相变汽化有关的现象。因此,由以上分析可得水在PBX-01炸药爆轰产物的驱动下,未发生相变汽化。
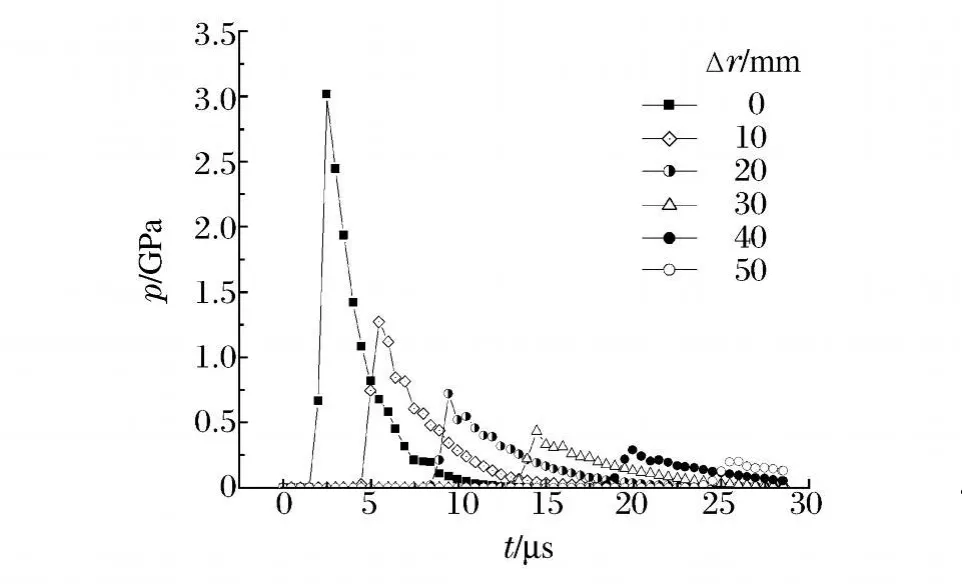
图6 压力历程Fig.6 Histories of pressure

图7 轴向速度Fig.7 Axial velocity
根据实验测得的爆轰产物驱动水介质膨胀的分幅底片,采用大型工具显微镜进行判读,得到不同时刻水界面膨胀轨迹的位移-时间曲线,从而获得中心点爆轰产物膨胀的轴向速度和径向速度,其中径向速度为所选择的基准点相对于基准像的膨胀速度(忽略了轴向速度的影响)。节点44 389的轴向速度如图7所示,计算结果与实验结果基本一致;节点44 410的膨胀径向速度如图8所示,计算结果与实验结果也基本一致。通过冲击波迹线的发展过程、爆轰产物膨胀的轴向和径向速度等实验结果与模拟结果的比较,说明数值计算所选用参数是适宜的。
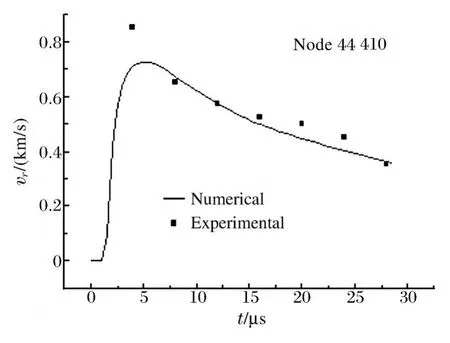
图8 径向速度Fig.8 Radial velocity
4 结 论
(1)采用阴影照相技术能够可靠获得炸药爆轰产物驱动水初期过程的图像;
(2)在炸药爆炸初期,水中的冲击波迹线与爆轰产物的形状相似,但冲击波迹线很快演变为类似球形,后期与爆轰产物的形状基本无关;
(3)通过实验、数值模拟和理论分析表明,水在爆轰产物作用下的最高瞬间温度为约342 K,尚未达到水在实验压力条件下的相变汽化温度;
(4)本文中采用的实验和计算方法也可用于研究炸药爆轰产物驱动其他液体介质内界面的初期发展过程。
[1] 薛里,颜事龙.爆炸水雾降尘机理探讨[J].安徽理工大学学报(自然科学版),2004,24(增刊):93-97.
XUE Li,YAN Shi-long.Discussions on the mechanism about dust-reduction using explosive water mist[J].Journal of Anhui University of Science and Technology(Natural Science),2004,24(supple):93-97.
[2] Abrahamson G R.Explosive dissemination from spherical devices[R].AD 804-6221,1996.
[3] Glass M W.Far-field dispersal modeling for fuel-air-explosive devices[R].SAND 90-0528,1990.
[4] 贵大勇,王海福,冯顺山.固液装药结构的FAE爆炸抛撒试验研究[J].弹箭与制导学报,2002,22(2):42-49.
GUI Da-yong,WANG Hai-fu,FENG Shun-shan.Experimental study on explosive dispersion of solid-liquid fuels for FAE devices with a special charge structure[J].Journal of Projectiles Rockets Missiles and Guidance,2002,22(2):42-49.
[5] 姚干兵,解立峰,刘家骢.水爆炸抛撒成雾的研究[J].弹箭与制导学报,2006,26(3):113-116.
YAO Gan-bing,XIE Li-feng,LIU Jia-cong.Investigation on the explosive dispersion process for water cloud[J].Journal of Projectiles Rockets Missiles and Guidance,2006,26(3):113-116.
[6] 胡栋,韩肇元,张寿齐,等.炸药爆炸变形和首次破碎的研究[J].高压物理学报,2004,18(3):198-202.
HU Dong,HAN Zhao-yuan,ZHANG Shou-qi,et al.Studies on explosion distortion and first break down under explosive detonation[J].Chinese Journal of High Pressure Physics,2004,18(3);198-202.
[7] Samirant M.Dynamic measurements in combustible and detonable aerosols[J].Propellants,Explosives,Pyrotechnics,1989,14:47-56.
[8] 郭学永,惠君明,解立峰,等.燃料爆炸抛撒过程的实验研究[J].高压物理学报,2005,19(2):25-31.
GUO Xue-yong,HUI Jun-ming,XIE Li-feng,et al.Experimental study on the process of fuel explosive dispersion[J].Chinese Journal of High Pressure Physics,2005,19(2):25-31.
[9] 龙新平.VLW爆轰产物状态方程及纳米含铝炸药爆轰特性研究[D].北京:北京理工大学,1999.
[10] Lee E,Breithaupt D,Mcmillan C,et al.The motion of thin metal walls and the equation of state of detonation products[R].Albuquerque,NA,USA:Lawrence Livemore National Laboratory,1985.
[11] Walsh J M,Rice M H.Dynamic compression of liquid from measurements on strong shock waves[J].Journal of Chemical Physics,1957,26(4):815-823.
[12] 彭福泉.实用非金属材料手册[M].吉林:吉林科学技术出版社,1991:389.
[13] Walsh J M,Christian R H.Equation of state of metals from shock wave measurements[J].Physical Review,1955,97(6):1544-1556.
[14] 李梦龙.化学数据速查手册[M].北京:化学工业出版社,2003:223.
