一种针对频率分配问题的改进ANTS算法

徐 奇,熊 晖,李 钊,陈大勇

(1.国防科技大学,湖南长沙410073;2.第二炮兵驻石家庄地区军事代表室,河北石家庄050081)

0 引言

在现有的频率分配算法中,模拟退火算法和蚁群算法[1]得到了广泛应用。模拟退火算法在Mettropolis原则的基础上允许做一些使目标函数增大的“上坡式移动”(Uphill Moves),以便解能从绝大多数局部驻点中脱离出来,具有快速全局搜索的特性,但它不能利用系统的反馈信息,这导致了过多的无用迭代和求解效率的低下。而ANTS算法通过信息素的积累和更新实现了分布式、平行搜索和全局收敛,在求解FAP问题时,表现出非常好的特性。但由于在初始阶段信息素的缺乏,同样存在着收敛时间过长的缺点,参见文献[2]。

为了克服每个算法的局限,同时充分利用它们的优点,本文提出了一种新的针对FAP问题的算法。首先,利用模拟退火算法在规定时间里求解FAP问题,利用它的快速收敛特性获得一组次优解。然后,利用获得的次优解来分配初始的信息素。最后,利用ANTS算法的平行搜索和正反馈特性来求解最佳解。

1 基于频率分配的算法

1.1 ANTS算法

1.1.1 算法原理

ANTS算法的主要元素是 ants——独立得、反复地构造问题的解的简单计算代理;求解过程中问题的部分解决方案被称为states(状态);每只蚂蚁从状态a转移到状态b,相应得构造了一个更加完整的局部解决方案。在每一步,每一个蚂蚁k都会计算出它当前状态的可能扩展状态,然后依概率相应的移动到下一个状态。对每只蚂蚁k,从状态a移动到状态b的概率Pkab依赖于动作的吸引力μab(由表明动作先验概率的启发式信息计算出来)和动作的轨迹水平 τab(表明在之前选择该动作的收益,也即该动作的后验概率)2个值的联合,参见文献[4]。

轨迹在每一个迭代之后都进行更新,增加好的方案的组成动作的轨迹水平,同时降低那些不好方案的动作的轨迹水平。在每一个动作,定义概率分布的相应公式都会用到tabuk,它指出了每一个蚂蚁每一次选择的禁忌动作。

在每一个时间,m只蚂蚁形成一个群体,完成一个方案。每一只蚂蚁完成方案的相应动作的轨迹水平由下式改进:

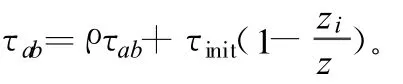
式中,系数ρ的函数(1-ρ)表明在2个方案形成过程中轨迹水平的衰减程度;τinit为轨迹信息素水平的初始值;¯z为之前由算法构造的L个方案的平均动作代价(当不足L个方案时则少于L个),而zi为蚂蚁k构造的第i个方案的代价。如果zi低于¯z,则构成该方案的动作的轨迹信息素水平相应得就增加,否则就减少,即保证了只有好的动作的信息素水平才增加(在蚂蚁的实际寻优过程中没有相应的这种机制)。

1.1.2 局部搜索

当每一个蚂蚁构造的方案完成后,在对其评价赋值之前,都会运用一个本地搜索程序(LS)来改善方案质量。通过不断试验验证,以下2种更新方案比较快速、简单和易于实现[4]:

①LS1:随机选择方案中得某一台站(发射机),然后选择频率域中的频率替换该台站(发射机)频率,如果替换后的新方案在代价上优于原方案,则用新方案替换旧方案,否则保留原方案。反复这一过程,直到所有的台站被选择一遍;

②LS2:所有的台站(发射机)都被反复扫描且以一定的概率w被选中。被选中的台站(发射机)进行随机排序且依此顺序被重新分配能使代价最小化的频率。同样在此搜索中,只有产生改进的方案才被保留,否则保留原方案。

在每一次迭代过程中,既可以单独使用LS1或者LS2,也可以把二者结合起来使用。譬如在前十分之一时间使用LS1而在后十分之九时间使用LS2(LS2效果更好而速度较慢)的。假设所需分配频点数为n,则一般m=n/10,ρ=0.4,τinit=0.7,ξ=0.7,参见文献[3]。

1.2 SA算法

一般的模拟退火算法的步骤如下:

①初始化,随机得到初始解,并计算代价cost;

②设置退火参数。分别设置初始温度T,冷却系数k,终止温度Tend;

③随机生成新个体,计算其cost′和cost′-cost=Δcost;如果 Δ cost＜0,则接受新解,否则以概率exp(-Δ cost/T)接受新解;

④使T=KT,如果T＞Tend或在规定迭代次数内解无停滞现象,则转步骤③,否则算法终止。

1.3 改进的ANTS算法SA-ANTSLocal

在ANTS算法的基础上对其进行改进,产生了一种新的SA-ANTSLocal算法。首先,利用模拟退火算法(SA)生成一个次优解,对次优解分配初始信息素,再利用ANTS算法寻找全局最优解。整个算法流程如图1所示。

图1 SA-ANTSLocal算法流程

在步骤①中的函数SADistribute伪代码如下:

τab=0

For(m solutions)do

{

τab=C+τab;

}

应用local optimization procedure寻找局部最佳方案时,本文使用的是LS1。在LS1中,对每一个台站采用穷举的方法来选择它的最佳频率。为了进一步缩短收敛时间,对LS1进行了改进。步骤如下:

①计算每只蚂蚁搜索得到的方案中所有台站的违约数,并依从大到小的顺序进行排序;

②按排序顺序选择违约数最大的P个台站,对每个被选择台站,依次选择频率域中的频率替换原频率。如果替换后得到的新方案优于原方案,则该方案替换原方案,否则保留原方案。

在改进的local optimization procedure中,关键是步骤2中P的选择。P选择过小则局部寻优得到的不一定是局部最优方案,P选择过大则起不到缩小收敛时间的作用,造成很多无谓的迭代。在下面的试验中,将进一步探讨P的选择。

2 算法测试

2.1 问题描述

2.1.1 FAP问题描述

FAP是典型的最佳分配问题,即利用有限的信道在满足如下电磁兼容约束限制的条件下,进行充分分配:

①同信道约束:相同的信道不能同时分配给某些小区;

②临信道约束:某些相邻的信道不能同时分配给相邻小区;

③同址约束:某些间隔较小的信道不能同时分配给同一小区。

根据实际的应用,常将频率指配问题从优化目标的角度分为4类:最少频点频率分配问题、最低阻塞概率频率分配问题、最小跨度频率分配问题和最小干扰频率分配问题。本文中主要从最少频点和最小干扰的角度来考虑。

信道分配问题可以用图着色问题来描述,因为图着色问题是N-P问题,所以信道分配问题也是N-P问题,它获得最佳解的时间随着解决问题的规模而指数性增长。

2.1.2 Philadelphia实例

比较智能优化算法的重要指标关键看2个方面:是否收敛以及在单位时间内的收敛率。为了验证SA-ANTSLocal算法的有效性,采取存在公认理论边界值的Philadelphia实例(21小区模型)为测试对象,参见文献[4]。21小区模型是最早研究的实例之一,是典型的蜂窝网络移动通信模型,每个小区都由一个基站与大量的移动台组成,通信方式为双工方式,基站分别与每个移动台之间占用一对频点,用正六边形表示小区,每个小区需要一定数量的频点,由于干扰具有对称性,也即基站与基站的频率约束间隔同移动台与移动台之间的频率约束间隔是相等的,故可取待分配主体为基站,移动台分配的频点只需在基站频点的基础上加一固定间隔即可。该问题的实例可由需求向量D、约束矩阵C、同频复用距离d、相邻小区频率间隔acc来描述。需求向量D表示的是各个小区的所需分配的频点数,约束矩阵C表示的是小区之间的约束关系。21小区问题具体的实例数据参考文献[4]。

2.2 试验仿真和结果

为了验证算法的有效性,针对典型21小区问题分别利用模拟退火算法(SA)、蚁群算法(ANTS)和改进的混合算法(SA-ANTSLocal)进行仿真,选取其中典型的6个问题,且对每个问题都限制用理论最小信道数进行分配。仿真是在CPU位Intel Celeron M 723 1.20GHz,内存为1 G的计算机上进行,采用Matlab语言编程,对上述算法分别进行10次仿真,每次迭代次数为30次。其中,若实例中待分配台站数为L,一般P设为L/2。仿真结果如表1所示。

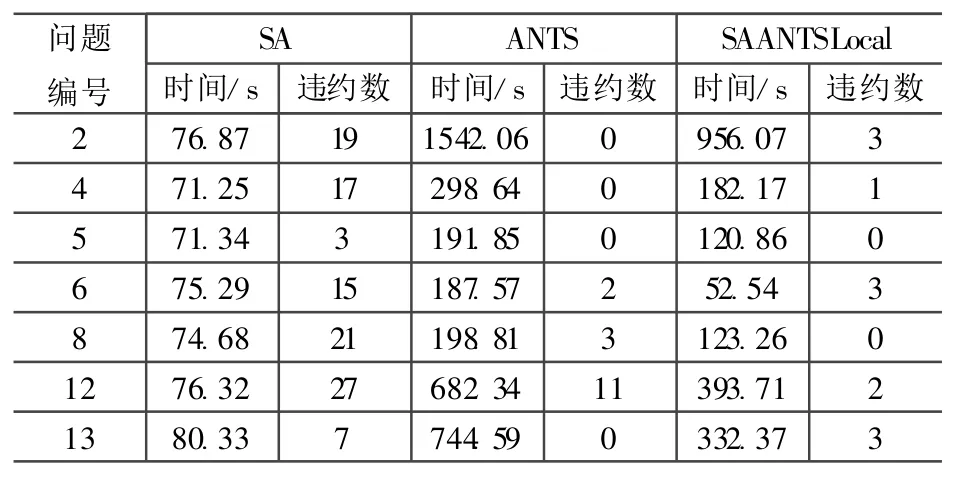
表1 4种算法的仿真结果比较

从表1可以看出,SA算法收敛时间最短,但很难得到最佳解,只有在极简单的情况下才能得到可用解。收敛时间由低到高依次是SA、SA-ANTSLocal、ANTS。其中,在解质量相当的情况下,SA-ANTSLocal要比ANTS算法节约大概1/3～1/2的时间。尤其在可用频点数较宽裕、对解质量要求不是特别高的情况下,可以通过设定P值的大小,进一步缩短收敛时间。

3 结束语

本文针对FAP问题提出了一种结合模拟退火算法的ANTS算法。与模拟退火的算法相比,该算法能够较好地避免陷入局部收敛,特别是在解决较难较复杂的频率分配问题时能取得更优的分配结果。与单纯的ANTS算法相比,该算法在保证一定的收敛率和违约数情况下,明显加快了运行速度,能较快得到分配结果。该算法不仅适用于频率分配问题,还可以应用到其他优化问题中。该算法有待在实际工程中进一步验证。

[1]COLORNI A,DORIGO M,MANIEZZO V.An Investigation of Some Properties of an Ant Algorithm.Proc.of the Parallel Problem Solving from Nature Conference(PPSN'92)[C].Brussels,Belgium:Elsevier Publishing,1992:509-520.

[2]MANIEZZO V.Exact and Approximate Nondeterministic Treesearch Procedures for the Quadratic Assignment Problem[J].Inform.J.Computing,1999,11(4):358-369.

[3]THAVARAJAH A,LAM W H.A Heuristic Algorithm for Channel Assignment in Cellular Mobile Systems[J].IEEE Transactions on Vehicular Technology,1998,45(6):1690-1694.

[4]MONTEMANNI R,SMITH D H,ALLEN S M.An ANTS Algorithm forthe Minimum-span Frequency-assignment Problem With Multiple Interference[J].IEEE Transactions on Vehicular Technology,2002,51(5):949-953.