一种基于输入缓冲交叉开关的调度算法
2010-06-14宣二勇王蕴珠
宣二勇,王蕴珠
(1.中国电子科技集团公司第五十四研究所,河北石家庄050081;2.河北大学计算机中心,河北保定071002)
0 引言
随着Internet中业务量爆炸性增长以及链路传输速率的不断提高,能够线速完成IP包转发与交换的网络核心设备,特别是核心路由器和交换机已成为制约网络性能的主要瓶颈之一。Crossbar开关因其固有的非阻塞特性以及易于实现等特点,被广泛应用于高速交换系统的研究和设计中。Crossbar开关主要用于ATM交换系统的设计,采用固定长度的信元交换方式,变长的IP包在输入端口被分割为多个固定长度的信元,通过交换开关后在输出端口处再被重组为变长的IP包。
开关结构和调度算法影响甚至决定着Crossbar开关的性能,因此采用合适的开关结构和高效的调度算法将成为设计高速大容量交换设备的关键。
1 系统模型
一个N×NCrossbar开关具有N2个交叉点,通过交叉点的闭合与断开可以同时完成N个信元的并行传输。根据缓冲区位置的不同,Crossbar开关分为输入缓冲和输出缓冲,输入缓冲Crossbar开关由于其内部交换速率只要求为输入链路速率,具有良好的扩展性,非常适合大容量高速交换系统的要求,因此得到了广泛关注和应用。
然而采用单一先入先出(FIFO)缓冲方式的输入缓冲Crossbar开关存在着严重的队头阻塞,队头阻塞表现为当队头信元得不到调度时,排在其后的所有信元均得不到调度,即使该信元发往空闲输出端口。队头阻塞使得开关的最大吞吐量仅仅为58.6%[1]。研究表明,采用虚拟输出排队(VOQ)策略可以完全消除队头阻塞:在每一个输入端口为每一个输出端口分配一个单独的队列,这样送往不同输出端口的信元被缓存在不同的队列中,从而各输入队列中的信元之间相互不会产生阻塞。
本文研究的模型采用基_于VOQ的输入缓冲Crossbar开关,如图1所示。
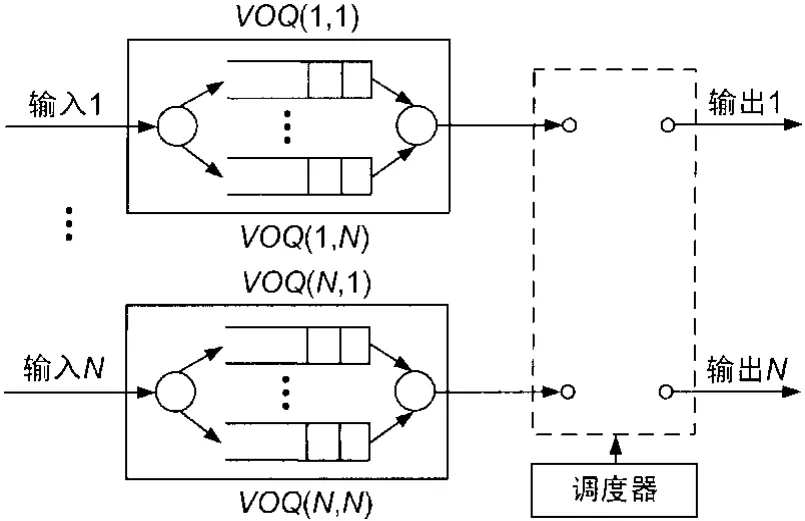
图1 基于VOQ的输入缓冲Crossbar开关
2 PB-RRM2算法分析
输入缓冲Crossbar开关需要高效调度算法的支持。调度算法的作用为在每一信元时隙产生配置信息以决定哪一个输入端口与哪一个输出端口相连。算法的设计基于如下原则:即每个信元时隙,任意一个输入端口至多可以发送一个信元,同时任意一个输出端口至多只可以接收一个信元。在实际的交换系统设计中,算法应高效简单,即算法在尽可能短的时间内应产生尽可能多的匹配,同时易于在硬件中实现。
衡量调度算法性能的主要指标[2]包括吞吐量、信元平均时延和公平性。
2.1 优先级列表
在并行迭代匹配算法中,Round Robin指针需按照一定的规则进行修改,合适的指针修改规则可以保证算法具有较少的迭代次数、更高的吞吐量和好的公平性。本文采用一种称为优先级列表 Round Robin指针修改规则,使得算法具有较高的性能。优先级列表的构造原则如下:
①如果输入端口Ii是输出端口Oj的第k优先级,则输出端口Oj也是输入端口Ii的第k优先级;
②一个输入端口只可以是一个输出端口的第k级优先级,同时一个输出端口只可以是一个输入端口的第k级优先级。
根据上述原则,优先级列表的产生方法为:假设{I1,I2,…,IN}和{O1,O2,…,ON}分别是输入端口和输出端口的集合,若输出端口Oj是输入端口Ii的第k优先级,1≤i,j≤N,则
k=((j+N-i)modN)+1。
由上式可知,起始时输入端口Ii分别是输出端口{Oi,Oi+1,…,Oi-1}的第i优先级,反之输出端口Oj分别是输入端口{Ij,Ij+1,…,Ij-1}的第j优先级。
根据优先级列表的构造方法,Round Robin指针修改原则如下:
①第i次调度时,输入输出端口的Round Robin指针位置处于优先级列表的第i条主对角线上,这样保证了在N次调度中任意一输入输出端口对将有一次调度过程中成为最高优先级匹配对,从而保证了算法的公平性;
②在每次调度的每次迭代过程中,输入端口从当前指针位置开始根据优先级列表按照从左到右的顺序选择非空的VOQ发送请求;输出端口同样从当前指针位置开始根据优先级列表按照从下到上的顺序授权接收到的请求信号;
③前面迭代中已匹配的输入输出对在后续迭代中不参与调度,未匹配的输入输出端口在后续迭代过程中继续参与调度,直到找到极大匹配。
2.2 算法步骤
现有调度算法如并行迭代匹配(PIM)算法[3]、iSLIP[4]算法等,每次迭代包含请求、授权和接受3个步骤。本文通过将请求和接受2个步骤进行合并,提出了一种2步调度算法,算法步骤如下:
①每个未匹配的输入端口按照Round Robin指针的优先级指示向一个空闲输出端口发送一个请求;
②如果一个空闲输出端口接收到任何请求,它根据Round Robin指针的优先级指示,接受具有最高优先级的输入请求,并通知所有输入端口该请求是否被接受;
③每次调度完成后,按照优先级列表的规则修改Round Robin指针,即次高优先级修改为最高优先级,而最高优先级修改为最低优先级。
PB-RRM2算法与已有的迭代算法的相比,一方面,由于在请求阶段每个输入端口仅产生一个请求信号,因此当该请求被授权时即意味着该输入端口与某一输出端口建立了匹配,从而算法将原先的3步迭代减少为2步迭代,缩短了每次调度所需的时间,从而提高了开关的运行速度。另一方面,由于输入和输出端口的指针采用优先级列表的方式进行配置和修改,保证了在每次迭代过程中输入端口和输出端口的Round Robin指针不会产生同步,提高了开关的吞吐量。
2.3 算法特性
通过上述对算法的描述,总结出PB-RRM2算法特性如下:
①算法采用2步迭代方式,缩短了每次迭代的时间,提高了开关的运行速度,非常适合于高速交换系统的设计中;
②由于在每次迭代中,每个输入端口仅发送一个请求,从而大大减少了输入输出端口间的交互信息,简化了输入输出端口仲裁逻辑的硬件设计,减少了所需的硬件逻辑资源;
③由于输入输出端口的Round Robin指针在每次调度后均被修改,保证了指针之间不会产生同步,因此消除了指针同步产生的吞吐量下降问题[5];同时可以证明当采用一次迭代时,PB-RRM2算法的吞吐量要大于iSLIP算法;
④由于N次调度中,任意(Ii,Oj)总会在某次调度期间成为具有最高优先级的输入输出对,从而算法不会出现“饿死”现象,保证了算法的公平性;
⑤可以证明,算法在独立同分布keepfull到达条件下,即任何时刻所有的VOQ不空时,一次迭代获得的吞吐量可以达到100%。
3 性能仿真
3.1 均匀分布
由于当输入链路速率较高时,调度的时间长度将受到限制,因此算法在实现中一般采用固定次数的迭代算法,下面的仿真结果给出了固定次数迭代算法的性能指标。
假设各输入端口的信元到达服从独立同分布(i.i.d)贝努利过程,负载为 λ,采用 16×16端口的Crossbar开关;同时假设每一输入端口到达的信元均匀地分布于各输出端口,算法每次调度迭代2次。
PB-RRM2算法和iSLIP算法在均匀的独立同分布贝努利到达条件下带宽利用率和信元平均时延的比较如图2所示。
由图2(a)可见,2种算法在λ<0.55时带宽利用率基本相同,这是由于当λ较小时,算法均类似于随机匹配。而当λ>0.55时,PB-RRM2算法的带宽利用率大于iSLIP算法。
由图2(b)可见,当λ<0.8时,2种算法具有几乎相同的信元平均时延,而当λ>0.8时,2种算法的信元平均时延呈现突发性增长,但PB-RRM2算法的信元平均时延要比iSLIP算法小得多。
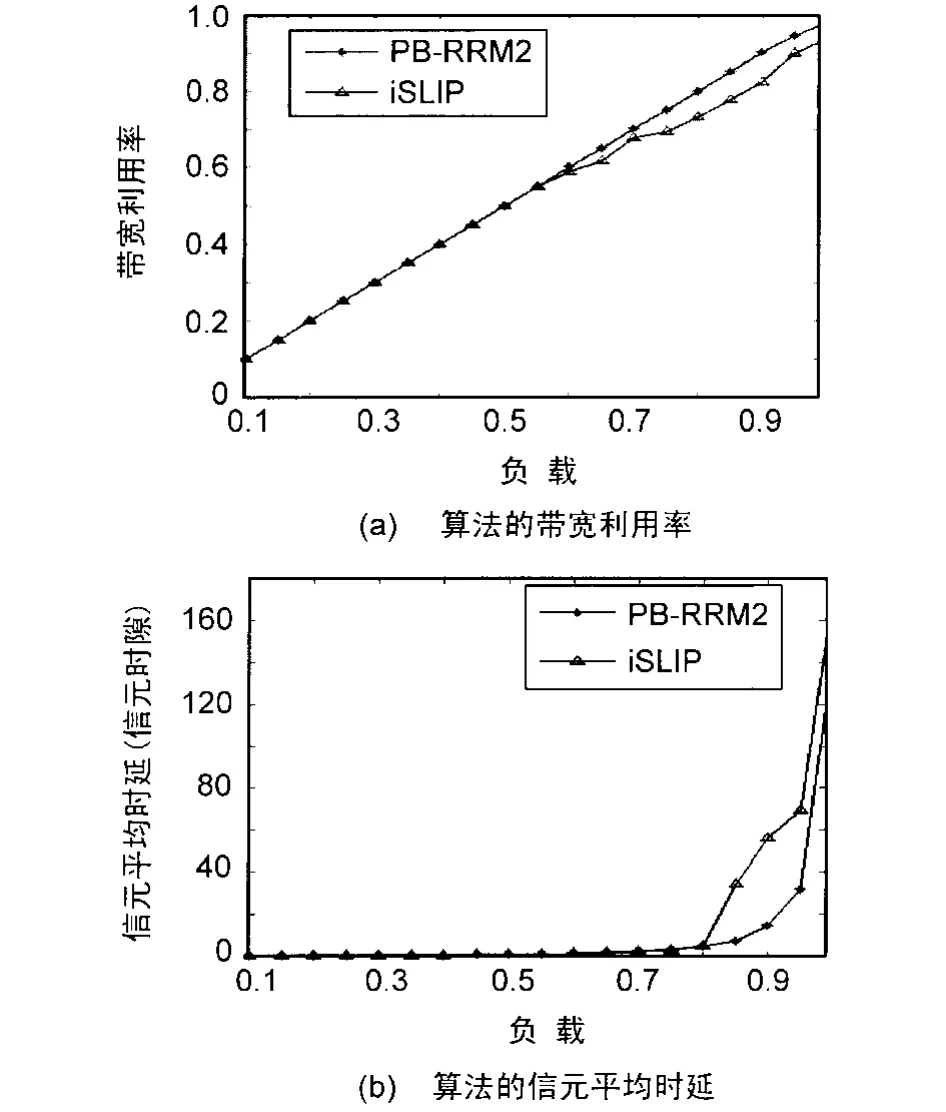
图2 i.i.d条件下的带宽利用率和信元平均时延
3.2 突发分布
PB-RRM2算法和iSLIP算法在突发到达情况下的吞吐量和信元平均时延如图3所示。
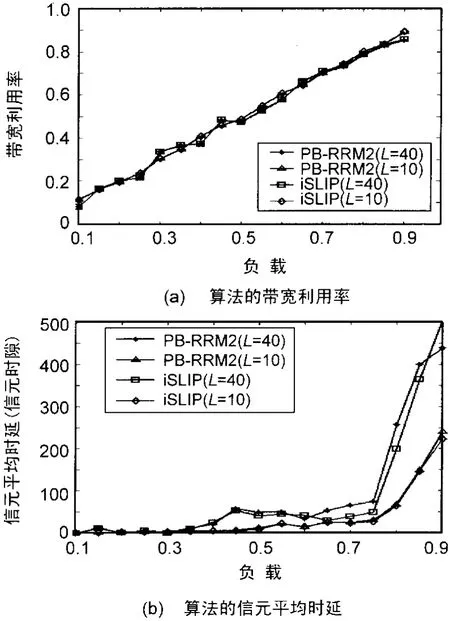
图3 on-off条件下的带宽利用率和信元平均时延
假设业务到达服从on-off过程,负载为λ,同时假设每次突发产生的信元具有相同的输出端口,突发长度L分别为10个和40个信元。
由图 3可以看出,在 on-off到达条件下,PBRRM2算法和 iSLIP算法的带宽利用率基本相同。而由图3(b)可见,当λ<0.6时,PB-RRM2算法的信元平均时延与iSLIP算法基本相同,当λ>0.6时,PB-RRM2算法的信元平均时延要稍>iSLIP算法。同时可以看出信元平均时延随着突发长度L的增加而增大。
4 结束语
在基于VOQ的Crossbar开关的基础上提出了PB-RRM2调度算法,通过计算机仿真表明,在均匀的独立同分布贝努利到达条件下,当负载较重时,该算法的性能要优于iSLIP算法,在突发到达条件下,2种算法的性能基本相同。PB-RRM2由于采用了2步迭代和基于优先级列表的Round Robin指针配置方式,减少了每次调度的时间,提高了开关的运行速度,同时消除了现有的Round Robin算法中由于指针同步所带来的吞吐量下降问题;另外根据算法2步迭代的运行方式相同这一特点,整个交换开关的设计中只需要一组Round Robin指针,减少了硬件逻辑资源。当采用流水实现时,算法硬件设计简单,非常适合大容量高速交换系统的应用场合。
[1]KAR OL M J,HLUCHYJ M,MORGAN S.Input Versus Output Queueing on Aspace Division Switches[J].IEEE Trans.on Communications,1988,35(4):1347-1356.
[2]孙志刚.路由器高速交换开关调度算法的研究实现[D].长沙:国防科技大学,2000:5-6.
[3]ANDERSON T E,OWICKI S S,SAXE J B,et al.High Speed SwitchScheduling for Local Area Networks[J].ACM Trans.on Computer Systems,1993,11(4):319-352.
[4]MCKEOWN N.The iSLIP Scheduling Algorithm for Input Queued Switches[J].IEEE/ACM Trans.Networking,1999,7(2):188-201.
