复杂电磁环境下跳频信号检测及拼接算法

方 志,贾 峰

(1.中国电子科技集团公司第五十四研究所,河北石家庄050081;2.空军驻石家庄地区军事代表室,河北石家庄050081)

0 引言

作为一种低截获概率技术,跳频数据传输具有较好的抗干扰性、安全保密性和组网能力,采用跳频技术的各类收发信机得到了广泛的应用,也向数据传输对抗提出严峻的挑战。开展对跳频信号侦察的研究,寻求截获跳频信号的方法,对于当前数据传输对抗具有重大的意义。

目前跳频信号检测技术的主要分析方法有自相关检测法、信道化接收法和时频分析法等。其中,时频分析法用于分析跳频信号有很大优势。但是在复杂电磁环境下,定频干扰信号的存在严重影响了对跳频信号的检测性能。因此,提出了一种针对跳频信号中的定频干扰信号进行频谱对消的方法,并将其作为跳频信号检测的预处理环节。该方法能较好地抑制定频干扰信号,提高跳频信号的检测概率。

跳频信号自动拼接是对已知参数的跳频信号在指定中频上完成拼接处理。这是介于网台分选和跳频信号解调之间的过程,其关键技术为时域校时,需要准确计算出每一跳信号的起始时刻和终止时刻进行信号提取,但是在低信噪比和时域信号包络不唯一的条件下,往往会有较大的校时误差。在大量仿真研究的基础上,提出了一种补零法则,能很好地克服这一难点,大大提高校时精度。

1 跳频信号检测

在复杂电磁环境下,跳频信号中常见的背景信号有定频信号、突发信号和随机噪声信号等。定频信号主要指连续定频信号与断续定频信号;突发信号主要指偶尔出现的信号;随机噪声信号主要指信道中各种噪声及接收机噪声信号。因此,如何有效地检测出该波段的跳频信号问题,就转化为如何有效地剔除其他信号的问题。

1.1 STFT跳频分析

采用短时傅里叶变换(STFT)来进行时频分析,给定一个时间宽度很短的窗函数 η(t),让窗滑动,则信号的短时傅里叶变化定义为:

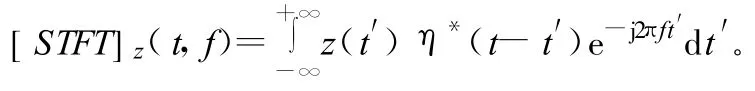
由定义式可见,信号z(t′)在时间t的短时傅里叶变换就是信号z(t′)乘上一个以t为中心的“分析窗”η*(t′-t)所做的傅里叶变换。由于乘一个相当短的窗 η*(t′-t)等价于取出信号在分析点t′=t附近的一个切片,所以短时傅里叶变换直接是信号z(t′)在“分析时间”t附近的“局部谱”。为了去除边缘效应,各段之间应有一些重叠,一般取FFT点数的一半,这样既有很好的效果也不至于运算量太大。

由于在时间t的STFT是被窗函数η*(t′-t)预加窗后信号z(t′)的谱,所以位于以时间t为中心的局部窗间隔内的所有信号特性都会在时间t的STFT内显示出来。因此,STFT的高时间分辨率要求一个较短的窗η*(t′-t);另一方面,STFT的高频率分辨率要求一个窄带分析窗,根据不确定性原理,时间分辨率和频率分辨率互相矛盾,所以只能牺牲时间分辨率以换取更高的频率分辨率,或反过来用频率分辨率的牺牲换取时间分辨率的提高。

1.2 跳频检测处理

跳频数据传输中载波频率变化的规律称为跳频图案。设R为跳频信号的跳速,p为占空比,则跳频周期Ts=1/R,跳频驻留时间TH=Ts×p。

应用STFT对某跳频信号进行时频图分析,图1(a)是时频图上某个时间点的原始频谱图,图1(a)中1、3为定频干扰,2为跳频信号,可见在复杂电磁环境下跳频信号中含有大量的定频干扰信号,并且定频信号可能存在于某一跳的频带内,这样就为跳频信号的时频检测带来困扰。此外,在频域上噪底呈现出不均匀分布,这样就使跳频信号的检测门限难以确定,为了达到较好的检测效果,必须对复杂的电磁信号环境进行处理,去除定频干扰和均匀化噪底。

跳频检测处理算法:首先将[STFT]z(t,f)二维频谱数据以非线性形式表示,并设时间分辨率为Δt;将[STFT]z(t,f)每个时间点上的频谱数据以ΔT的间隔时间前后进行对消处理,其中 ΔT=T/Δt(TH＜T＜Ts),考虑到可能存在连续两跳信号在同一频点上,因此需要将每个时间点上前后对消的结果进行比较,保留较大的对消值;通过时频图功率谱的非线性对消处理,不仅可以很好地去除定频干扰,而且还能改善噪底,使噪底趋于均匀。但是,频谱非线性对消处理会使噪底的抖动变大,将真实信号淹没,为了弥补这一缺点,加入二维中值滤波处理,不仅可以平滑噪声,还大大改善了信噪比,使真实信号很好的凸显出来,提高了信号的检测概率。

跳频信号检测处理结果如图1(b)所示,与图1(a)相比,可见频域上存在的大量定频干扰和其他一些噪声干扰经过频谱非线性对消处理已经完全被去除,并且噪底在频域上均匀分布,便于检测门限的确定。该处理算法较传统的时频分析方法可以有效地解决跳频信号和定频信号发生频谱碰撞时,跳频信号的检测问题,并且处理过程简单易于硬件实现,对于工程中在现代战场复杂电磁环境下,进行电子侦察处理具有一定的实际意义。

图1 频谱对消前后时频图上某时间点的频谱图对比

2 跳频信号拼接

跳频信号自动拼接是介于网台分选和跳频信号解调之间的过程,目的是将已知跳频参数的跳频信号在指定中频上完成拼接,以便于后续的解调处理。跳频信号自动拼接的处理过程可以简述如下:

首先从原始采样数据中检测出已知参数的跳频信号,然后通过校时算法准确计算出每一跳信号的起跳时刻和终止时刻,并进行信号提取,此外还需要测量出每跳信号的中心频率,用于下变频处理。

2.1 校时算法

跳频信号自动拼接处理的关键是进行时域校时,通常采用计算斜率求拐点的方法来实现。简述如下:

首先将两跳时长的跳频信号在频域上进行滤波处理,由此在时域上可以得到跳频信号的包络,并将包络进行积分。将积分后的信号分别对起始点和终止点求斜率,在2次处理结果中最大斜率处称为包络的左右拐点,即为跳频信号准确的起跳时刻和终止时刻。

2.2 补零法则

在低信噪比条件下,信号包络很不平滑,并且由于滤波阶数较小或相邻跳在同一频点上等原因,使得时域上信号包络并不唯一,这样就使校时结果存在较大的误差,为后续的解调处理带来困难。为了解决这一难题,通过大量仿真研究发现在进行校时处理时,采用前后补零的方法来延长数据的长度,可以精确定位出拐点的位置。根据校时时可能存在的种种情况,推算出补零法则的范围公式:

计算左拐点时:

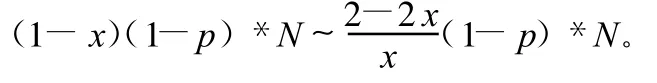
计算右拐点时:

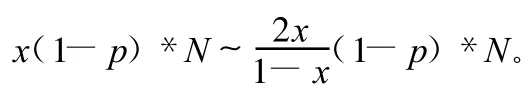
式中,0≤x≤1表示校时时可能存在的不同情况,p(p≠1)为占空比,N为一跳信号的时长,如图2所示,若要准确确定出图中所示的拐点位置,需要在数据的前后补充一定长度范围的零点。

图2 准确校时补零法则

2.3 校时效果

根据跳频检测结果提取一段跳频数据(至少包含一个完整的跳频信号)进行校时,根据补零法则一般取补零范围的中间值作为补零长度,在原始采样数据的前后添加相应长度的零点采样数据,然后将延长后的跳频数据根据校时算法计算左右拐点,定位跳频信号的起始时刻和终止时刻。

通过上述处理,得到的校时结果如图3所示。由图3(c)可以清楚地看到改进的校时算法计算出的拐点位置精确的定位到跳频信号的终止时刻上。因此,补零法则改进的校时算法可以很好的克服时域包络不平滑和信号包络不唯一的情况,实现校时误差为零,为后续解调处理奠定良好的基础。

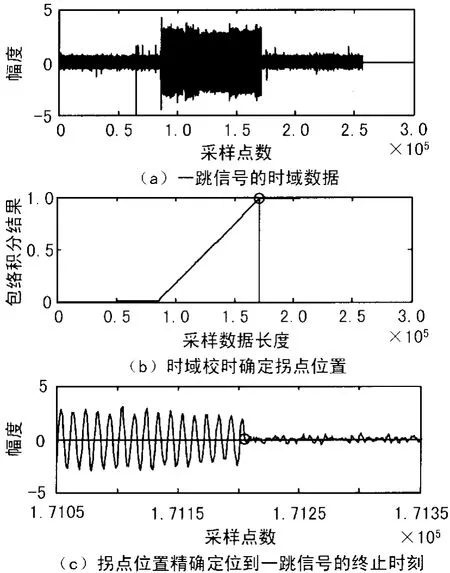
图3 改进的校时算法精确计算出一跳信号的终止时刻

3 结束语

基于时频图跳频图案进行功率谱非线性对消的跳频信号检测算法不仅可以去除跳频信号中的定频干扰,改善信噪比,还可以对不均匀的噪底进行均匀化处理,使跳频信号的检测概率大大提高。算法处理过程简单,易于硬件实现,适于在工程实践中应用,具有很高的推广价值。

同时,补零法则改进的校时算法可以精确定位拐点的位置,很好地克服时域包络不平滑和信号包络不唯一的情况,提高了校时精度。通过仿真验证,可以实现校时的零误差,为后续解调处理奠定了良好的基础。

[1]张贤达.现代信号处理(第2版)[M].北京:北京出版社,2002.

[2]张 丹,吴 瑛.STFT在跳频信号分析中的应用[J].计算机应用,2005(10):60-61.

[3]温晓敏,刘作学,代建美.复杂电磁环境中跳频信号检测算法研究[J].装备指挥技术学院学报,2008,19(6):100-103.