联台大桥部分斜拉桥振型分析

赵琦彦

0 引言

一般来讲,连续梁以受弯、受剪来承受竖向荷载,斜拉桥以梁的受压和索的受拉来承受竖向荷载,而部分斜拉桥由于采用了拉索的形式,通过索塔的高度将体内预应力筋移出梁体,使其与梁体形成了一个水平夹角。一方面,通过水平方向的分力形成偏心弯矩来帮助梁体受力,起到了预应力筋的作用;另一方面,通过竖直方向的分力抵消了梁体的重力,在梁体上形成了许多弹性支点,减小了梁体的“跨度”,起到了斜拉索的作用,所以它以梁的受弯、受压和索的受拉来承受竖向荷载。因此,其结构性能必然同连续梁桥和斜拉桥有所不同,是介于连续梁桥和常规斜拉桥之间的一种新桥型。

联台大桥属于部分斜拉桥,位于南安市福溪村,横跨西溪,跨越河槽部分主桥长300 m,两岸引桥长分别为33.50 m和63.5 m。桥面全宽为30.5 m(含构造跨度),双向六车道。梁体为单箱三室变高度斜腹板箱形截面,主跨(136 m)墩顶处梁高 4.5 m,跨中处梁高及边跨直线段采用2.6 m,中跨及边跨梁底曲线线型采用二次抛物线。桥塔为钢筋混凝土矩形截面,主跨塔高(梁顶以上17 m),塔柱均采用矩形截面,顺桥向长3.0 m,横桥向宽2.0 m。

1 计算模型

各主要组成部分在动力计算模式中的模拟方式分述如下:

1)箱梁计算模式。梁体模型采用壳单元(Shell63)来模拟,对于梁体、桥墩部分、桥塔均采用实际截面尺寸和形状建模,主梁刚度采用其实际刚度。2)斜拉索的计算模式。斜拉索采用空间杆单元模拟,考虑到其垂度引起的非线性,每一根索均按照Ernst公式进行了弹性模量折减。3)桥塔及桥墩的计算模式。为了考虑桥墩对桥梁动力特性的影响,动力分析模型中加入了桥墩部分,桥塔、桥墩均采用实体单元来模拟,并且梁与下部结构之间的连接采用耦合关系来处理。二期恒载化为均布荷载加在相应的节点上,得到了如图1所示的计算模型。

2 模态分析

基于上述斜拉桥有限元模型的建立,采用ANSYS大型有限元程序,进行了该桥的模态分析。表1列出了计算得到的前10阶振型频率、周期及振型的描述。

联台大桥主桥桥跨布置(82+136+82)m,单索面部分(矮塔)斜拉桥,单箱三室变截面预应力混凝土箱梁截面,桥宽30.5 m,塔梁固结,仅在3号墩设置了一个固定支座,其余为定向支座。2号,3号桥墩为薄壁实体墩柱。

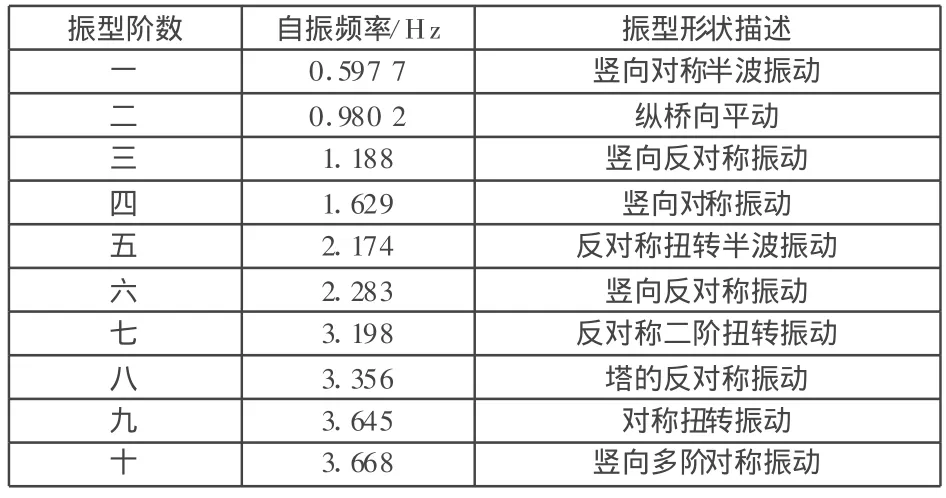
表1 联台大桥自振频率及振型特性

桥梁的第一阶振型频率ω1=0.5977Hz,相应振型为以主跨半波弯曲振动为主的竖向一阶对称振动。主跨为一个半波,两边跨各为一个半波。显现出桥梁跨度大、上部结构的高度较小而横向宽度又较宽,桥梁上部结构的竖向刚度与其横向、扭转及桥墩刚度相比较小,振型表现出对称的特点。

桥梁的第二阶振型频率ω2=0.9802Hz,相应振型表现为桥梁整体的纵向平动伴随着主梁一阶反对称竖向弯曲振动,振型频率比一阶频率提高64%,这是由于本桥塔梁固结,上部结构仅在3号墩设置了一个固定支座,且桥墩属于薄壁式桥墩,其纵向弯曲刚度较小,因而桥梁二阶振型表现为桥梁整体的纵向平动伴随着主梁一阶反对称竖向弯曲振动。显然,随着3号墩水平刚度的减小,二阶频率必然降低。

第三阶自振频率为ω3=1.188Hz,振型表现为一阶反对称竖向弯曲振动的特点,主梁呈现出四个半波,属二阶竖向弯曲振动,并伴随以3号桥墩为主的纵向弯曲振动。振型频率比一阶竖向提高98.8%。

桥梁的第四阶振型频率ω4=1.629Hz,相应振型表现为主跨结构的三阶竖向对称弯曲振动,全桥呈现出五个半波的振动特点。频率比一阶提高1.73倍。

桥梁的第五阶自振频率为ω5=2.174Hz,相应振型表现为主梁主跨一阶半波反对称扭转振动。振动频率比一阶竖向振动频率竖向基频高2.64倍。桥梁主跨箱梁的一阶扭转振动在主梁竖向对称、反对称弯曲振动和桥梁整体的纵向平动之后出现,充分反映出桥梁单箱三室斜腹板预应力混凝土箱梁抗扭刚度大的特点。

桥梁前5阶振型,随频率的提高主梁竖向一、二、三阶竖向振动,纵向一阶平动,扭转振动交错出现,说明桥梁整体上竖向和扭转刚度均衡,同时反映出桥梁上部结构构造对称的特点。

桥梁的第六阶自振频率ω6=2.283Hz,振型表现为边跨结构为主的二阶竖向反对称弯曲特点,主跨和边跨呈现出两个半波的振动态势。频率比一阶提高2.82倍。

桥梁的第七阶振型频率ω7=3.198Hz,相应振型表现为主跨的反对称二阶扭转振动的特点,频率比第一阶提高4.35倍。

桥梁的第八阶振型频率ω8=3.356Hz,相应振型表现为主塔的反对称面外或横桥向弯曲振动,说明本桥虽然是单索面桥梁,但由于其塔“矮”,横向弯曲刚度相对较大的特点,这也是区别斜拉桥的一个显著特点。频率比第一阶提高4.61倍。

桥梁的第九阶振型频率ω9=3.645Hz,相应振型表现为以梁的主跨三阶对称扭转伴随边跨扭转振动和主塔的对称横向弯曲振动的特点。桥梁的五、七、九阶振型分别为桥梁箱梁的一、二、三阶扭转振动,一方面说明本桥单箱三室箱梁扭转刚度大的特点,同时也反映出本桥桥面宽的特点。频率比第一阶提高5.09倍。

桥梁的第十阶振型频率 ω10=3.668Hz,相应振型表现为以主梁高阶竖向弯曲振动为主伴随塔的侧向弯曲振动的振动特点。频率比第一阶提高5.13倍。

3 结语

通过对前10阶振型进行分析,可以得到如下结论:从桥梁的前10阶振动频率和振型,各阶振动竖向、纵向及扭转的频率相差不大,桥的竖向一阶振动、纵向平动、竖向二、三阶振动、扭转振动、竖向多阶振动和对称、反对称振动交替出现,说明箱梁结构的梁高变截面曲线设置以及腹板的设置方式均在合理范围之内。梁的抗扭刚度的增大使扭转振型后移,这将有利于增强桥梁的抗风性能。由十阶振型没有出现整体横向弯曲振动的特点可知该桥横向刚度比较大。同时说明本桥有限元计算模型正确,边界条件模拟符合工程实际。

[1] 倪燕平.兰州银滩黄河大桥地震反应分析[D].兰州:兰州铁道学院硕士学位论文,1998.

[2] 郭继武.建筑抗震设计[M].北京:高等教育出版社,1991.

[3] 范立础.桥梁抗震[M].上海:同济大学出版社,1996.

[4] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.

[5] 沈志林.独塔单索面斜拉桥稳定性计算方法的探讨[J].铁道标准设计,2003(9):31-32.

[6] 范立础.桥梁抗震[M].上海:同济大学出版社,1997.

[7] 刘世忠,欧阳永金.独塔单索面部分斜拉桥力学性能及建设实践[M].北京:中国铁道出版社,2006:3.