实索振动试验中最低测点位置的初步研究*

张 鹏 淡丹辉

0 引言

近年来,斜拉桥作为一种美观实用的桥型受到广泛的青睐,拉索研究也日益深入。拉索振动试验是进行拉索模态分析、索力识别和振动控制的重要试验方法。但是,在实际的试验中,测点布置是有一定讲究的。本文主要研究内容就是探索拉索振动试验中测点的布置问题。为了解决上述问题,本文自建的有限元模型,通过振动理论分析得到FEM上几个典型节点的加速度功率谱密度谱,并且得到前几阶频率的PSD值沿索长的变化图,在理论上证明拉索振动试验时最低测点的存在;接着通过实索试验得到振动的加速度信号,并对信号进行频谱分析,得到加速度功率谱密度谱及PSD值沿索长的变化图,证明理论分析的正确性。

1 有限元模型理论分析

本文的有限元模型是建立在传统的有限元方法基础上[1-4],考虑轴力和弯矩影响的小应变几何非线性单元刚度矩阵的情况下,利用自编的有限元模型程序,对拉索进行模态分析,得到其加速度和位移的反应谱。在对拉索模型进行模态分析时,本文主要采用了虚拟激励法[5,6],并且假设地面激励为白噪声且为单点激励,那么根据结构动力学方程,离散化结构在地面加速度激励下,其表达式为:

在零初始条件下,设其单点激励的白噪声功率谱密度为S0,则对式(1)进行傅立叶变换得到:

由此,可以得到位移的功率谱与加速度功率谱:

为了与试验情况相比较,该拉索有限元模型中的各项参数均取试验拉索的实际值,索的线密度 96.85 kg/m,索长95 m,初始张拉索力146 t,索的直径125mm,材料的弹性模量2.0×1011Pa,索的内阻尼比为2%。

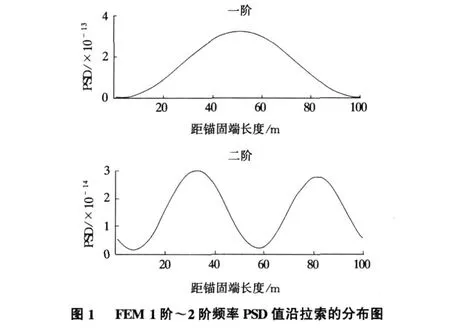
由频差法求得拉索振动的基频为 f=0.7 Hz,则1阶～2阶各阶频率的PSD值沿索长的分布图见图1。从图1中可以看出,PSD值在索端均是从小到大变化。因此,拉索振动试验中最低位置的测点理论上是存在的。

2 实索试验分析

为了进一步证实理论的正确性,本文安排了一个在广西柳州欧维姆机械股份有限公司进行的实索试验,实索参数同上述理论分析实例,两端锚固。试验时,4个加速度传感器布置在距离锚固端2 m,7 m,12 m,17 m的地方,其编号分别为1,2,3,4,试验过程中不做任何人工激励,且没有任何外部阻尼器,仅测量在大地脉动作用下拉索的振动信号。试验时间设定为20min,采样频率为25.6 Hz。对加速度信号进行分析[7]。

3 理论分析与试验数据对比

3.1 基频比较

由频差法得到理论与试验基频值分别为0.7 Hz和0.82 Hz,相对误差为14.6%。其原因主要是拉索模型参数与实索有差异,需要进行模型修正。有限元分析中的拉索参数是理想化的取值,与实际有差别会对理论值与实测值的比较产生差异。

3.2 PSD值沿拉索变化趋势比较

由理论分析,拉索1阶～4阶频率的PSD值在达到第一个峰值时所在的位置应该对应于索的1/2,1/4,1/6,1/8处。在实索试验时,对应的点应分别为距锚固端47.5 m,23.75 m,15.83 m,11.875 m处。从图2可以看出前三阶的PSD值的变化均是从小到大,而第4阶频率的PSD值在测点距锚固端12 m处达到峰值。但是由于试验条件所限,测点布置过于稀疏,因此对3阶,4阶频率的PSD值的第一个峰值左右的情况描述不够细致,趋势是吻合的。

4 结语

从理论分析可知,对拉索第 n阶频率,其PSD值在索的(2m-1)/2n(m=1,2,…,n)处达到最大值,在索的(m-1)/n(m=1,2,…,m+1)处取值为零。因此,在实索试验当中,传感器应该放置在PSD值峰值附近,且尽量避免靠近PSD值取零的区域。在后续试验中,可对传感器的布置进行加密,得到更加精确细致的拉索PSD值沿索的分布情况,进而得到测量时索噪声较大区域的范围,为试验测点布置提供经验。在后续理论分析中,要建立更加符合实际的有限元模型,并且进行索在不同的荷载(如风、地震)下索PSD值分布的研究。

[1] 张运波,沈锐利.单索结构振动特性的有限元分析[J].公路,2002(10):46-49.

[2] 王焕定,吴德伦.有限单元法及计算程序[M].北京:中国建筑工业出版社,2001.

[3] G.Ricciardi,F.Saitta.A continuousvibration analysis model for cables with sag and bending stiffness[J].Journal of Sound and Vibration,2008(317):127-141.

[4] H.M.Irvine.Cable Structures The MIT Press,Cambridge,MA,1981.

[5] 林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004.

[6] Lin J H,Zhang W S,Williams F W.Pseudo-Excitation Algorithm for Non-Stationary Random Seismic Responses Engineering Structures,1994(16):270-276.

[7] 乔陶鹏,严普强,邓 焱,等.斜拉索索力估算中振动信号处理方法的改进[J].清华大学学报(自然科学版),2003,43(5):644-647.