电磁炮发射轨道受指数函数磁压力的变形计算
2010-06-06白象忠张海军
刘 文,李 敏,白象忠,张海军
(1.燕山大学理学院,河北秦皇岛 066004,liuwen1961@hotmail.com;2.燕山大学建筑工程与力学学院,河北秦皇岛 066004)
电磁炮发射轨道受指数函数磁压力的变形计算
刘 文1,李 敏1,白象忠2,张海军1
(1.燕山大学理学院,河北秦皇岛 066004,liuwen1961@hotmail.com;2.燕山大学建筑工程与力学学院,河北秦皇岛 066004)
为解决电磁炮发射轨道受力变形的精确计算,以利于延长导轨的使用寿命并提高发射精度,将某型电磁炮的发射轨道模拟为移动载荷作用下弹性基础上的简支梁,采用欧拉梁理论建立梁的力学模型,推导出受任意指数函数磁压力控制方程的解析解,改变了长期以来利用均布压力近似代替变力求解问题所造成的误差;运用MATLAB软件对弹性基础的弹性系数、阻尼系数、轨道质量和载荷的出口速度对梁变形的影响进行了数值分析.结果表明,弹性基础的弹性系数、移动载荷的出口速度对梁变形的影响比较显著,阻尼系数、轨道质量的大小对梁变形没有明显的影响.为求解电磁炮发射轨道受任意函数的磁压力作用时的变形以及推动电磁炮的实用化奠定了理论基础.
电磁炮;发射轨道;欧拉梁;指数函数磁压力;拉格朗日方程;解析解
电磁炮是一种全新概念的武器,其技术不仅在军事领域,而且在航空、航天、交通运输、工业生产、科学研究等领域具有不可估量的应用前景,各发达国家均从战略高度予以重视并不断加大力度开展研究.80年代以来,尤其是最近十年来,随着新技术、新材料的不断发展,电磁发射技术在发射装置、发射重量、弹丸速度、大功率电源等方面的研究取得了一系列成果.美国的苏伦斯·利弗莫尔国家实验室和洛斯·阿拉莫斯国家实验室曾合作,将2.2 g的弹丸加速到10 km/s的超高速.中国工程物理研究院流体物理研究所率先建造了我国第一台电磁轨道发射试验装置,把0.34 g的弹丸加速到16.8 km/s.相比之下常规火炮的发射速度仅能达到2 km/s,这一速度已接近物理极限,使射程不可能更远.相反电磁发射系统的推力比火药发射的推力大10倍,能把弹丸加速到每秒几公里至每秒几十公里的高速度,使弹丸具有巨大的动能和极强的穿透力,从而大大提高了武器的射程和威力[1-3].
T.Tzeng[4]采用弹性基础梁作为电磁发射装置轨道的力学模型,并给出了控制方程的数值解.胡宇伟[5]针对电磁轨道炮的工作过程进行了理论剖析、模型建立及仿真分析.王胜[6]采用了傅里叶变换研究了空间上欧拉梁表面移动荷载引起的位移场的计算.
上述的研究都将磁压力近似为均布力并忽略了阻尼力对梁变形的影响,毫无疑问,这种情况的计算都存在力学分析和计算时的缺陷.作为高技术高精度的电磁发射装置,工程上要求对其进行精确的理论分析与计算,然而,至今尚未有人给出其精确的解析解,“非线性问题没有通解,而且历史上得到的一些特解少得如同珍宝.”[7]因而推出变压力之解析解是非常有意义的.事实上,各学科中的理论解析解,包括工程实际问题的解析解,都是非常有意义的.一方面它可以全面彻底地阐明它所表达的力学图景,另一方面它可作为标准解,促进广泛应用的各种数值解的产生.
本文考虑了阻尼力,并将轨道作为弹性基础上的简支梁,建立了移动载荷作用下的力学模型[8-9],利用分离变量法和计入阻力的拉格朗日方程,推导出控制方程的解析解,并对弹性基础的弹性系数、阻尼系数、轨道的质量以及移动载荷的出口速度对梁变形的影响进行了数值分析.
1 力学模型
图1给出了由电源、导轨、电枢组成的电磁轨道发射装置的工作原理示意图.电流经过导轨、电枢后流回电源,构成闭合回路.流经导轨、电枢的电流在它们围成的区域内形成强磁场,该磁场与流经电枢的电流相互作用,产生强大的电磁力,该力将推动电枢和置于电枢前的发射载荷沿着导轨作加速运动,直至将发射载荷发射出去.
图2为该问题的力学模型——弹性基础上受随时间变化的非线性载荷作用的简支梁.考虑阻尼力对梁的影响,根据欧拉梁理论,得到移动载荷作用下的弹性基础梁的控制方程为一个瞬时四阶微分方程[10]:
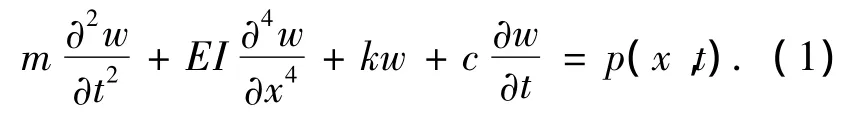
其中w为梁的挠度,m=ρbh为梁的单位长度的质量,ρ为轨道材料的密度,b和h分别为轨道梁横截面的宽和高度,EI为该梁的抗弯刚度,k为弹性基础的弹性常数,c为弹性基础的阻尼系数.式(1)中的函数p(x,t)=q(x)[1-(x-vt)]是指以速度v沿着轨道向前传播的电磁力,v由Heaviside单位阶跃函数 H(x- vt)表示[11],q(x)=q(abx+c).

图1 电磁轨道发射装置发射原理简图

图2 模拟成弹性基础梁的轨道力学模型
2 齐次方程的通解
齐次方程为一个四阶偏微分方程,采用分离变量法求解,目的是使问题转换为常微分方程.
式(1)所对应的齐次方程的通解可表示为

把式(2)代入式(1)的齐次方程得

也可以表示为如下的形式:

由式(4)假设

和

即

式(5)的解可以表示为

其中
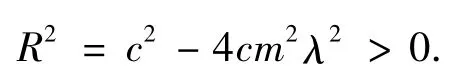
根据简支梁的边界条件

式(7)的解可以表示为[12]

因此

由于 θi(x)的正交性[13],满足
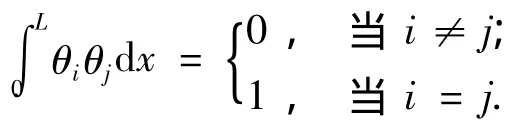
w(x,t)可以表示成θi的线性组合,即

其中Ai,Bi可以由初始条件确定.
3 控制方程的解析解
式(1)的解析解可以由下面的计入阻力的拉格朗日方程求得,其中T为梁的动能,U为梁的总变形能,G为耗散函数.

梁的动能T可以表示为[14]

梁的总变形能由梁的应变能Ub和弹性基础的应变能Uf组成.
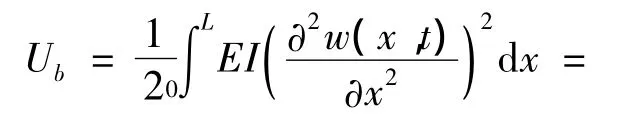

总的变形能U为

耗散函数G为
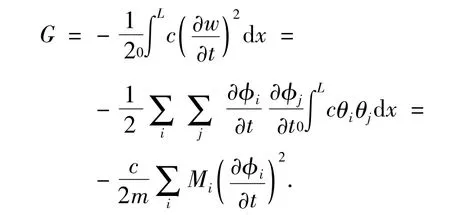
电磁力 p(x,t)=q(x)[1 -H(x-vt)]在虚位移δφi下所做的虚功可以表示为
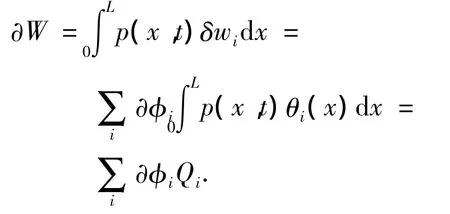
其中Qi表示广义力

将T,U,G,Qi代入计入阻力的拉格朗日方程,可以得到微分方程:
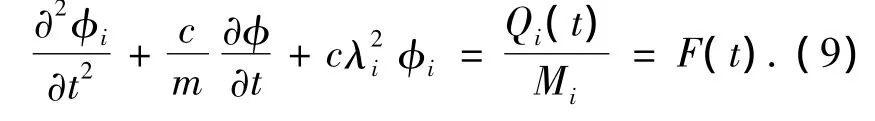
其中
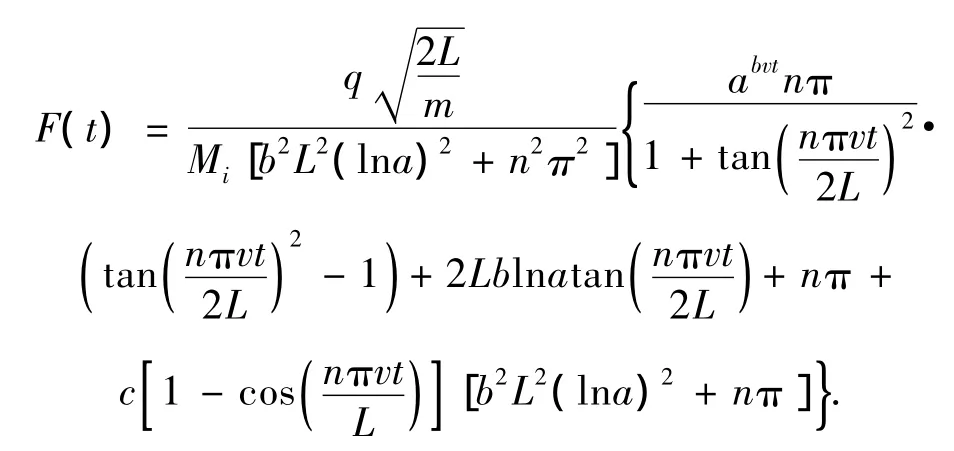
式(9)的通解为

由此,式(1)的解可以表示为

由初始条件
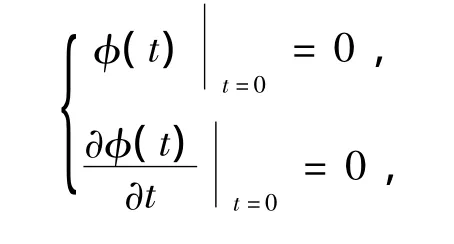
有

因此,将式(11)的解代入到式(10)就可以得到方程(1)的解 w(x,t).由 w(x,t)可以进一步得到轨道上的弯矩和剪力,为更全面地讨论电磁发射装置的动力响应提供依据.
4 数值分析
由于电磁轨道发射装置制作材料的差异,弹性基础的弹性系数和阻尼系数、轨道的质量以及载荷的出口速度可能会对轨道的变形产生影响[15],因此有必要对其作比较分析.
已知轨道材料[16]的杨氏模量E=120 GPa,弹性基础的弹性系数k=2.532×1010Pa,轨道材料的质量密度ρ=8 700 kg/m3,截面宽度b=3×10-2m,高度 h=1×10-2m,轨道长度为 L=2 m,电磁载荷q(x)=110sin(1/2)x MPa.
图3给出了弹性基础的弹性系数对梁的动态响应[18-19].时间 - 挠度曲线随着弹性系数 (k)的增加而呈下降的趋势.在本文所给的计算条件下,k=2.532×1010Pa的材料在t=1×10-3s时,梁的挠度(w)为7×10-3m,而 k=5.064×1010Pa的材料在 t=1×10-3s时,梁的挠度(w)为3.4×10-3m,前者比后者增加了106%.

图3 不同弹性基础的弹性系数下的挠度变化图
图4给出了弹性基础的阻尼系数对梁的动态响应.时间-挠度曲线随着阻尼系数的增加而呈缓慢下降的趋势.

图4 不同弹性基础的阻尼系数的挠度变化图
图5给出了轨道质量(m)对梁的动态响应.对比铝轨道与铜轨道,时间-挠度曲线随着m的增加并没有出现明显的变化,因此,在选择轨道的材料时,可以选择性价比更优的铝材料.

图5 不同轨道质量下的挠度变化图
图6给出了载荷的出口速度对梁的动态响应.时间-挠度曲线随着载荷移动速度(v)的增加而呈增加的趋势,在本文所给的计算条件下,v=1 000 m/s的材料在t=1.6×10-3s时,梁的挠度(w)为8×10-3m,而v=1 200 m/s的材料在t=1.6×10-3s时,梁的挠度(w)为 12.5×10-3m,前者比后者减小了56%.

图6 不同载荷出口速度下的挠度变化图
5 结论
1)考虑了非线性磁压力及阻尼力,将轨道看作是弹性基础上的简支梁,建立了电磁发射装置的力学模型.
2)利用分离变量法和计入阻力的拉格朗日方程,推导出齐次方程的解及受指数函数分布压力控制方程的解析解,丰富和发展了弹性力学理论,为解决电磁轨道受任意分布压力之解析解的难题奠定了理论基础.
3)通过MATLAB软件分别进行了地基的弹性系数、阻尼系数、轨道质量和载荷的出口速度对梁变形的影响:地基弹性系数越大,梁变形的越小.载荷的出口速度越大,梁的变形越大,而梁的质量和阻尼系数对梁的变形几乎没有影响.
[1]SMITHA N,ELLISR L,BEMARDEJ S,et al.Thermalmanagement and resistive rail heating of a largescale naval electro - magnetic launcher[J].Trans on Magnetizes,2005,41(l):235 -240.
[2]FAIR H D.Progress in electromagnetic launch science and technology [J].Trans on Magn,2007,43(1):93-98.
[3]FAIR H D.Electromagnetic launch science and technology in the United States enters a new era [J].Trans on Magn,2005,41(1):158 -164.
[4]TZENG J T,SUN Wei.Dynamic response of cantilevered rail guns attributed to projectile/gun interaction-theory[J].Transactions on Magnetics,2007,43:207 -213.
[5]胡玉伟.电磁轨道炮系统的建模与仿真[D].哈尔滨:哈尔滨工业大学,2007.
[6]王胜.弹性半空间上欧拉梁表面移动荷载引起的位移场[D].哈尔滨:哈尔滨工业大学,2007.
[7]郑哲敏.郑哲敏文集[M].北京:科学出版社,1994.
[8]LIU Wen,SHAN Rui.Mathematic model and analytic solution for a cylinder subject to exponential function[J]. Chinese Journal of Mechanical Engineering,2009,22(4):587 -593.
[9]LIU Zhubai,SHAN Rui,LIU Wen,et al.Solution of a hollow thick-wall cylinder subject to quadric function pressures and its limit when l→∞ [J].Science in China(Series E),2004,47(2):229 -236.
[10]于艳丽.移动载荷作用下轨道系统和高架桥的动力响应分析[D].武汉:武汉理工大学,2002.
[11]TZENG J T.Structural mechanics for electromagnetic railguns[J].Transactions on Magnetics,2005,6:247-249.
[12]朱石坚.振动理论与隔振技术[M].北京:国防工业出版社,2006:36-66.
[13]张相庭,王志赔.结构振动力学[M].上海:同济大学出版社,2006:93-117.
[14]娄平,曾庆元.移动载荷作用下连续粘弹性基础之承无限长梁的有有限元分析[J].交通运输工程学报,2003,3:1 -6.
[15]TZENG J T.Dynamic response of electromagnetic railgun due to projectile movement[J].Transactions on Magnetics,2005,41:246 -250.
[16]JOHNSON1A J,FRANCIS C.Elastic waves and solid armature contact pressure in electromagnetic launchers[J].Transactions on Magnetics,2006,3:472 -475.
Deformation calculation of electromagnetic Launcher’s rail subjected to exponential magnetic pressure
LIU Wen1,LI Min1,BAI Xiang-zhong2,ZHANG Hai-jun1
(1.School of Sciences,Yanshan University,Qinhuangdao 066004,China,liuwen1961@hotmail.com;2.School of Civil Engineering & Mechanics,Yanshan University,Qinhuangdao 066004,China)
In order to accurately calculate of the force-deformation of electromagnetic launcher’s rail for the purpose of extending the rail life and improving the firing accuracy,the electromagnetic launcher’s rail was modeled as a simply supported beam on elastic foundation by moving load.The mechanical model of the beam was built by using Euler beam theory,and the analytical solution to the equation subjected to exponential magnetic pressure was derived,which can avoid the errors resulting from the uniform pressure used to replace the variable force.The influence of the elastic coefficient,the damping coefficient,the mass of rail and the load’s velocity on the deformation of beam was numerically analyzed with MATLAB.The result shows that the elastic coefficient and the load’s velocity have obvious effect on the deformation of the beam,while the damping coefficient and the mass of rail do not.The study lays a foundation for solving the electromagnetic launcher’s rail subjected to magnetic pressure of arbitrary function and promoting the practicality of the electromagnetic guns.
electromagnetic gun;launcher’s rail;Euler beam;exponential function magnetic pressure;Lagrange equation;analytical solutions
TJ399;O343.3
A
0367-6234(2010)08-1336-05
2008-11-27.
国家自然科学基金资助项目(50875230).
刘 文(1961—),男,副教授,博士研究生.
(编辑 刘 彤)
