反热源问题及其数值计算*
2010-06-05贾现正冯兆永
贾现正,冯兆永
(1.山东理工大学理学院,山东 淄博 255049;2.中山大学数学与计算科学学院,广东 广州 510275)
在本文中,我们将考虑下面这种类型的方程
其中Ω是Rn本身或者是Rn中的一个区域。我们讨论反热源问题,也即是反演函数g(x,t)的问题。反热源问题是一个很有实际价值的问题,例如在工程上,这个问题被用来确定湖水或河水水面的污染源。当然,作为实际的模型,我们必须考虑对流扩散反应方程,但是通过一个变换可以把这个模型转化为热传导方程。
对于反热源问题,已经有了很多结果。对于一般的热源项g(x,t),通过边界测量数据来确定它是很困难的。因此,我们往往对一些特殊的类进行研究。对于和时间无关的g(x,t)=g(x),Cannon[1]用谱理论,Engl等[2]应用近似可控方法进行了研究。在文[3]中,Yamamoto还把文[2]中
的结果推广到g(x,t)=α(t)f(x)的情况,其中α∈C1[0,T],α(0)≠0已知。Hettlich等[4]考虑了g(x,t)=χD(x)的情况,其中D是圆盘Ω的一个子集,他们证明了当测量了Ω的边界上的两个不同的点的数据,可以确定区域D,并且给出了数值算法。在文[5-6]中,考虑了g(x,t)是非线性函数的情况。
在本文中,我们考虑的是g(x,t)=f(t)φ(x)的情况,其中f(t)未知,φ(x)是一个具有紧支集的函数。在文[7]中,如果f(t)是个至多改变符号N次的连续函数,则可以得到一个Hölder型的稳定性估计,但是Hölder型稳定性估计不能给出唯一性。在本文中,我们对f(t)是分段常数的情况进行了研究,得到了一个Lipschitz型的稳定性估计,并且给出了数值计算结果。由于问题的不适定性,对带有误差的测量数据计算结果比较差,因此我们引入了正则化方法进行了计算。
为了简单起见,我们假设Ω∈C∞(见文[8])。考虑下面的问题
ut=Δu+f(t)φ(x),(x,t)∈Ω×(0,T)
(1)
u(x,0)=0,x∈Ω
(2)
u(x,t)=0, (x,t)∈∂Ω×(0,T)
(3)
其中φ是一个给定的函数,并且满足下面的条件
φ≥0且在Ω中不恒等于0
(4)
φ在Ω中有紧支集
(5)
给定
u(x0,t),0 其中x0∈Ω/suppφ。我们的主要任务就是得到未知的函数f(t),0≤t≤T,并且给出一个条件稳定性估计。 在文[7]中,为了得到条件稳定性结果,需要下面的不等式,这里我们简单叙述这些结果。 定理1 令p≥1,δ>0,0≤α 0≤f,g≤M<∞,0 则 ‖f‖Lp(α,T)‖g‖Lp(0,δ)≤ 特别地, 对α=0,有 在文[7]中,对Ω=Rn和f∈u得到了一个Hölder 型的估计。其中 u={f∈C[0,T];‖f‖C[0,T]≤M, fchanges the signs at mostN-times} 定理2 假设φ满足(4)-(5)以及下面的条件 φ∈C∞(Ω),ifn≥4 φ∈L2(Ω),ifn≤3 并且令 则任给δ>0,存在一个常数C=C(x0,φ,T,p,δ,u)>0,使得 对任意的f∈u都成立。 推论1 在定理2中,如果把Y换成 PN={f;f是一个阶数不超过N的多项式且‖f‖C[0,T]≤M} 则可以得到同样的结果。 注:定理2和推论1的结果是有缺陷的,结论中的Hölder型稳定性估计不能给出唯一性。 我们所感兴趣的是当f(t)是一个分段常数函数的情况,而在这种情况下,f(t)可以有无数个零点。对于这种情况,我们得到Lipschitz型的稳定性结果[9]。 对于问题(1)-(3)的解u(x,t),我们可以把它表示成下面的形式[10-11] x∈Ω,t>0 其中K(x,y,t)是问题(1)-(3)的基本解。关于这个表示形式可以参考文[11]。 同样地,从文[11]知道 K(x,y,t)>0,t>0 令 有 (6) 这是一个关于函数f的第一类Volterra型的积分方程。 下面考虑f∈F={f是一个[0,T]上的分段常数函数}的情况,得到如下结果。 定理3 (唯一性)对于问题(1)-(3)和已知的条件u(x0,t),如果函数f∈F,则除了有限个点以外,这样的f是唯一确定的。 按从小到大的顺序重新排列这些点,并且假设重排后的间断点序列为0=τ0<τ1<…<τI3=T,则对0 u(x0,t)-u(x0,t)=0 即 对于τ1 同样地可以得到f1(t)=f2(t),t∈(τ1,τ2)。因此重复上述步骤,可以得到f1(t)=f2(t),t∈(τj-1,τj),j=1,2,…,I3。这就得到了唯一性。 假设分段常数函数f在0=t0 定理4 (稳定性)如果φ满足条件(4)-(5),且x0∈Ω/suppφ。那么对任意p>1,存在一个常数C=C(x0,φ,T,p,F,δ)>0使得 ‖f‖Lp(0,T)≤C‖u(x0,·)‖Lp(0,T) 证明对于分段常数函数f(t),假设它在0=t0 由于μx0(t)是正的且有界,根据公式(6),有 取上式从0到t1的Lp模,得到 这样可以看到 f1|≤C1‖u‖Lp(0,t1) (7) 即 从而得到 ‖u(x0,t)‖Lp(t1,t2)+C2‖u(x0,t)‖Lp(0,t1)≤ C3‖u(x0,t)‖Lp(0,t2) 所以 f2|≤C‖u(x0,t)‖Lp(0,t2) 因此,由于ti-ti-1≥δ>0,i=1,2,…,I和(7)式,则有 ‖f‖Lp(0,t2)≤C‖u(x0,t)‖Lp(0,t2) 重复这个过程直到ti=T,从而得到了要证的结果。 对于问题(1)-(3),如果给定u(x0,t),我们需要重构函数f(t)。考虑下面的辅助问题 ut=Δu+φ(x),(x,t)∈Ω×(0,T) (8) u(x,0)=0,x∈Ω (9) u(x,t)=0,(x,t)∈∂Ω×(0,T) (10) 给定数据u(x0,ti),i=1,2,…,N,其中0=t0 i=1,2,…,N 假设f(t)=fi,t∈[ti-1,ti],i=1,2,…,N,则 从而,可以用上述公式来得到函数f(t)的离散解。 例1 选f(t)为下面的函数 选取Ω=(0,2),x0=1.5,φ(x)=1,x∈(0,1)且在(0,1)外面φ(x)≡0。给定数据u(x0,ti),i=1,2,…,N,则可以利用下面的公式来得到f(t)的数值近似 数值结果如图1,2所示。它们之间的误差如图3所示。 图1 数值计算的结果 图2 f(t)的真实解的图像 图3 误差 如果对测量数据加上2%的误差,可以看到计算结果会变得比较差,因此我们在下一节引入正则化算法来解决这个问题。 例2 现在给出一个二维情况下的例子,其中函数f(t)是一个分段常数函数,而且其中一段为零。假设问题同样是(1)-(3),区域Ω=(-1,1)×(-1,1),且 取x0=(0.7,0.8),T=3,数值结果如图4,5所示。 图4 数值计算的结果 图5 f(t)的真实解的图像 它们之间的误差如图6所示。 图6 误差 由于上面的数值算法对测量数据的误差非常敏感,也就是说测量数据即使只有很小的误差,而结果也会有很大的误差,因此,我们需要进行正则化处理,这里选取Tikhonov正则化方法。 对于上面的算法,离散后需要求解线性方程组Ax=b,而系数矩阵A是一个病态矩阵,因此可以对线性方程组实行Tikhonov正则化,来求解线性方程组(ATA+αI)x=ATb。假设给定数据的误差水平为δ,也即给定数据与实际数据之间的误差小于等于δ。故我们可以取α=δ2,参见文[12]。 数值例子:我们采用前一节的第一个例子,对给定数据加上2%的误差,并采用正则化的方法进行计算,数值结果如图7。 图7 正则化算法的数值结果 我们对热源项为f(t)φ(x)类型的反热源问题做了研究,其中f(t)是一个分段常数的函数。得到了这种带有特殊热源项情况的反热源问题的一个稳定性估计,并且对于这个问题提出了数值计算的方法并给出了数值例子以及正则化算法。 参考文献: [1] CANNON J R. Determination of an unknown heat source from overspecified boundary data[J]. SIAM J Numer Anal, 1968, 5:275-286. [2] ENGL H W, SCHERZER O, YAMAMOTO M. Uniqueness of forcing terms in linear partial differential equations with overspecified boundary data[J]. Inverse Problems, 1994, 10: 1253-1276. [3] YAMAMOTO M. Conditional stability in determination of densities of heat sources in a bounded domain, estimation and control of distributed parameter systems[M].Birkhäuser, 1994. [4] HETTLICH F, RUNDELL W. Identification of a discontinuous source in the heat equation[J]. Inverse Problems, 2001, 17: 1465-1482. [5] DUCHATEAU P, RUNDELL W. Unicity in an inverse problem for an unknown reaction term in a reaction-diffusion-equation[J]. J Diff Equations, 1985, 59: 155-164. [6] CANNON J R, DUCHATEAU P. Structural identification of an unknown source term in a heat equation[J]. Inverse Problems, 1998, 14: 535-551. [7] SAITOH S, TUAN V K, YAMAMOTO M. Reverse convolution inequalities and applications to inverse heat source problems[J]. J Inequal Pure and Appl Math, 2002, 3(5): Article 80. [8] ADAMS R A. Sobolev spaces[M]. New York: Academic Press, 1975. [9] IMANUVILOV O Y, YAMAMOTO M. Lipschitz stability in inverse parabolic problems by the Carleman estimate[J]. Inverse Problems, 1998, 14:1229-1245. [10] PAZY A. Semigroups of linear operators and applications to partial differential equations[M]. Berlin: Springer-Verlag, 1983. [12] CHENG J, YAMAMOTO M. One new strategy for a priori choice of regularizing parameters in Tikhonov's regularization[J]. Inverse Problems, 2000, 16: L31-L38.1 已有的结果


2 我们的结果

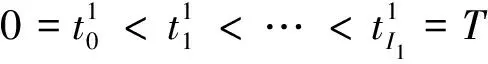






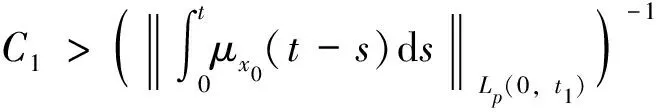






3 数值例子

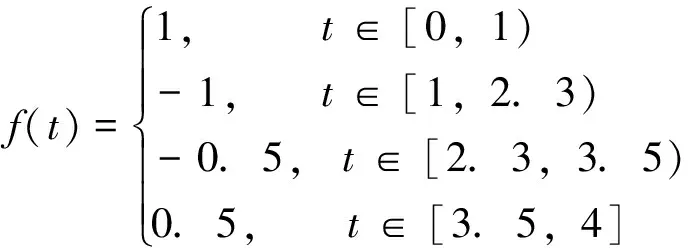








4 正则化算法

5 结 论
