管路连接中的约束设计(上)

李俊昇 文 放 刘 涛

（中航工业综合技术研究所，北京 100028）

1 问题的提出

约束分析是结构设计的重要内容，机械结构中的多数零件都是通过约束来确定其空间位置，再通过对约束的反作用来实现性能。管路系统设计中，约束同样是必须充分考虑的内容。在飞机和发动机管路设计中，由于对约束的分析不足，造成管系设计上的缺陷，会严重影响系统的可靠性与安全性。

采用管路的主要目的在于传递介质和介质压力（可能是正压也可能是负压）而不是作为结构承力件，从系统设计考虑，应在满足主要功能的前提下尽可能轻，所以，减少非介质压力的影响是管路设计优化的首要目标。

由于管路件的设计不是以参与结构受力为目的，所以与周围承力结构件相比，其抗拉压和抗弯扭强度和刚度都要弱得多。飞机和发动机都是弹性结构，在飞行中的结构变形很大，结构变形所产生的应力对较弱的冗杆影响最大，所以，一但导管成为结构中的冗杆，后果将是灾难性的。

除了机动载荷，装配过程中不可避免的工艺误差也会造成冗杆结构的初始应力，这对于导管来说同样可能是致命的。

因此，对于管路连接设计来说，精心设计约束状态，避免零件承受非介质压力引起的载荷，是提高系统可靠性与安全性的重要途径。

要达到上述目标，需要从连接件结构设计和管系布设设计两个方面共同努力。

2 刚性导管的基本约束模型

约束分析在机械结构初步设计和方案设计中是最简单也是最容易掌握的，但在实际设计中却少有人关注。在型号的管路系统设计中进行约束分析，是提高可靠性和安全性的一个简单可行的方法。

约束包括几何约束和力学约束，本文所讨论的约束属于几何约束。本文的目的，是为了提供一种简单的、容易掌握的定性分析方法。

一个固体一共有6个自由度，包括3个相互正交的轴向上的位移自由度和3个相互正交的轴向上的转动自由度，相应地就需要6个约束才能确定这个固体的状态。

如果约束的数量超过6个，就形成了过约束。过约束状态下，仅当所有约束间的空间尺寸完全协调时才不致造成固体上的静态应力。由于生产过程中特别是复杂装配体不可避免的误差和误差积累，这种完全协调的状态只在理论上存在，在实际产品上是不存在的。

对于需要避免结构应力的管路件来说，任何过约束都是不利的。但如果缺少了某个自由度，这个物体就成了自由体，在静态下，这固然不会导致固体中产生静态应力，但在存在振动或过载时，则可能产生冲击载荷，也不是我们所希望的。在某单位进行导管柔性连接件的脉冲试验时，就是因为在轴向上没有对试验件进行约束，因而导致连接提前破坏，这样的事如果发生在实际型号上，其结果可想而知。

不同轴不同类的过约束和欠约束是不能相互抵消的，这是约束的特点，是需要注意的。

管路最佳状态是相互正交的六约束状态。

见图1。假定有一根导管，它总是会有2个连接端A和B，导管的约束通常就是由这2个连接端提供的，在特殊情况下，还可能存在中间支撑来提供额外的约束C，我们把这3个部位的约束分别定义为约束组A、约束组B和约束组C，这就是一根刚性导管的基本约束模型。

图1 刚性导管的基本约束模型

所谓管路连接的约束设计，就是在保证管路基本功能（密封）的前提下，为每根导管提供恰到好处的6个约束，或者说将6个约束以最合理的方式分配给每根导管的各个约束组。

理论力学中的约束是以支撑来表示的，一般是以简单的刚支、铰支、滑支的方式描述，这种描述方法通常已经组合了多种约束类型，管路连接约束分析需要用进行更细致的划分，才能满足需要。

为此，我们在任一约束点定义迪卡尔坐标系xyz。这样，该点处的约束就可分为沿3个轴向的位移约束（Sx、Sy、Sz、）和沿3个轴向的转动约束（Rx、Ry、Rz），分别对应导管的6个自由度，其他位置的约束可以通过矢量分解的方法折算到这3个轴向。

约束虽然通过力而起作用，但与力并不是相同的概念。力是约束作用的方式，是有数值的，并与零件的材料直接相关，而约束则是一种边界条件，只取决于零件的几何特征，与材料无关，它是独立于力而客观存在的。管路连接的约束均是双向约束，因此我们在表示约束的时候，用双向的箭头表示更能体现它的特点。

约束是没有大小的，只有零和非零两个状态，我们把不为零约束定义为1，并可以进行算术加减。

两个同轴向的位移约束会因其轴线间的距离不同而表现为不同的约束形式，距离越短，则趋向于位移过约束，距离越远，则趋向于以约束偶的形式形成转动约束。

两个或多个位移约束是形成过约束还是形成转动约束，可以通过将这些约束用矢量分析法分解到3个相互正交的轴向上的方法进行分析，此时，其中一个轴要通过两约束组的作用点，如存在不止2个作用点时，需要逐对分析。如图2。

位移约束在作用点连线方向上的分量的算术和决定其是否过约束，分量和为0时欠约束，分量和为1时是有效约束，分量和大于1时为过约束。

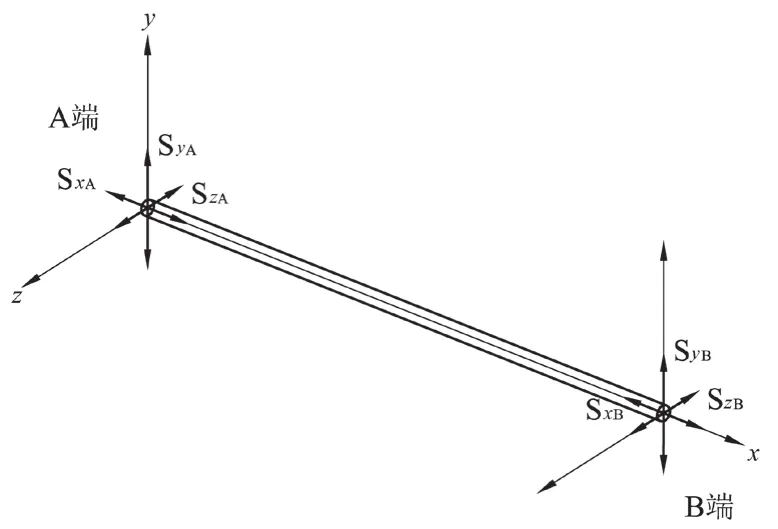
图2 简单两支点约束分析

与作用点连线方向正交的2个轴向上，约束分量的和为0时欠约束，为1或2时时形成有效位移约束，为2时以约束偶的形式形成一个有效转动约束。

约束偶的方向与两平行约束分量平面正交。

转动约束由距离足够大的约束偶提供时是最有效的，也可以仅由某一点的刚性固定构成，但在受力上是不良的，同时，同一轴向上的约束偶与支点自身的转动约束也将构成过约束。

图2中所表示的是由2个位置（A点和B点）的完整位移约束所共同构成的约束体系，经过3轴向分析可以知道：

x轴：位移约束SxA和SxB，和为2，过约束，记为S＋x；

y轴：位移约束SyA和SyB，和为2，构成有效位移约束和一个约束偶，记为Sy和Rz；

z轴：位移约束SzA和SzB，和为2，构成有效位移约束和一个约束偶，记为Sz和Ry。因此，总约束状态为S＋

x、Sy、Sz、Rz和Ry，为一个位移过约束且欠一个转动约束的状态。

上述约束状态在两端均为全向铰接支撑的简支梁结构中是通用的，与被支撑零件的形状无关，如果希望实现6个有效约束状态，需要将任一端的X方向位移约束消除，同时增加该轴向上的转动约束Rx。

导管的基本约束模型（图1）通常包括两点约束和三点约束两类，两端点的约束组一般是必不可少的。

3 约束机理与补偿性

导管连接中，约束均是通过零件间相互接触的表面实现的，如果2个零件间存在一对不相正交的接触面，因而限制在2零件间在某一空间方向上的相对运动，就构成了约束。一般来说，由于接触表面可以只有一个，所以约束也可以是单方向的，但对于管路连接来说，均为对称结构，单方向的约束并无实际价值，所以在讨论管路连接时，我们所定义的约束均是双方向的。

可以根据形成约束的力的形式来划分约束特性，也就是说：如果约束是以表面正压力而发生作用，则这个约束可理解为在表面的法向空间上不可移动，把这种约束定义为强约束；如果约束是以表面摩擦力的形式发生作用，则这个约束可理解为在卸去正压力后可以沿表面切向滑移，把这种约束定义为弱约束；如果不存在可以构成约束的正压力或摩擦力，则称为零约束。

单一接触表面对的接触状态，可以在构成位移约束的同时构成转动约束，这决定于接触面在某一方向上的接触尺寸。接触尺寸足够大，则认为在接触点的切面上，与这个尺寸正交的方向存在转动约束，否则就不存在转动约束。

根据上述定义，可以发现，如果某个结构是通过有足够接触宽度的圆锥面和与之同轴的端面共同构成连接时，除沿圆锥轴线方向是转动弱约束外，其余的5个约束均是强约束。

所谓补偿性或补偿能力，就是2个配合零件间在某个方向上的相对移动能力，可以分为动补偿、静补偿和无补偿3种。任何情况下均可移动时称为有动补偿性或能力，仅在未施加安装预紧力的条件下才能移动时称为有静补偿性或能力，任何情况下均不能移动的称为无补偿性或能力。

补偿性与约束特性是一一对应的，强约束对应的是无补偿性，弱约束对应的是静补偿性，零约束对应的是动补偿性。

绝对的强约束和绝对的零约束一般在实际结构中并不存在，因此绝对的补偿性在实际结构中一般也不存在。当约束力与相应方向上的结构强度（包括疲劳强度）相比足够小时，我们就认为是零约束，当接触应变与相应方向上的结构破坏（包括疲劳破坏）变形相比足够小时，就认为是强约束。

而补偿性也是有条件的，这个条件就是结构提供的相应方向上的位移空间，所以，如果要严格地定义补偿性，还必须加入补偿量条件，比如：“在x轴方向上相对端面在（+3～+18）mm范围内可补偿。”但在本文的分析中，我们均假定在某个方向上全尺寸可补偿。

当在某一个方向上存在多个同类约束时，并不就意味着过约束，此时还要看各约束的特性如何。如果在这些约束中最多只有一个强约束，其他均为弱约束，此时的约束是静补偿性的，因此应视为静态有效约束，但在动态载荷的作用下，弱约束也会发生作用，所以是动态过约束。如果在这些约束中强约束的数量超过一个，则无论静态还是动态都是过约束。

4 常用连接结构的约束

虽然我们希望尽可能实现六有效约束状态，但工程上导管的实际使用环境和条件是千差万别的，加上其他使用要求的限制，要完全达到理想的约束目的，仍然是有困难的。

法兰盘连接、扩口式导管连接、无扩口式导管连接，按照现在流行的叫法应该被称为刚性连接，与之对应的是柔性连接。

本文使用全约束连接和减约束连接的叫法，因为这更能体现连接结构的约束状态，更方便进行约束分析和约束设计。

刚性连接的特点是同时给导管提供6个约束，因此可称为六约束连接或全约束连接。柔性连接只提供2个约束（Sy和Sz），因此可称为减约束连接或两约束连接。还有介于两者之间的连接（球面连接和梁式密封连接），可根据具体约束数量命名或称为准刚性连接或准柔性连接。

过约束的数量越多，在结构中产生不良应力的可能性就越大，就越难控制。由于一根导管必有2个需要约束的连接端，所以只要任何一端采用全约束连接，就不可能实现最佳约束状态，而且没有好的补救办法，因此，刚性连接是最差的管路连接方式；两端均采用柔性连接时会出现欠约束，但这并不算糟糕，因为可以通过设计一个能提供余下的2个约束的中间约束组C来实现最佳约束状态。

由于导管连接中，密封是必须达到的功能要求，而密封本身需要在密封表面的法向上的强约束来解决，因此即使最好的导管连接结构，也需要至少一个强约束。

下面对不同导管连接结构的约束情况作一简单分析，为便于统一基准，我们约定连接端的导管轴向为x轴。

4.1 法兰连接

法兰连接有两类主要形式：整体式和压板式，见图3。从图中的结构形式可以看出，整体式法兰（图3（a）和（b））在任何情况下都是全约束，而且所有约束都是强约束，因此可称为强全约束。由于任何一个导管连接端都至少需要一个强约束，而采用整体式法兰时，便不可能没有过约束，所以整体式法兰对于导管连接来说永远都是不良结构。

压板式法兰如果采用非嵌入式结构（图3（c）），在螺栓未拧紧的状态下允许沿x轴转动和沿y轴、z轴的少量位移，但拧紧后这些自由度便不存在了，因此，它是一个三强三弱的全约束连接，其强约束为Sx、Ry和Rz，弱约束为Rx、Sy和Sz。

压板式法兰如果采用嵌入式结构（图3（d）），那么所有的位移自由度都被强限制，所以拧紧后就成为五强一弱的全约束连接，其弱约束为Rx。

可见，如果法兰连接是不得不采用的，也以非嵌入的压板式连接更好，或者，如果连接的密封面是端面的话，嵌入式连接的嵌入部分采用大间隙配合（此处指0.5mm以上），也可在配合间隙范围内形成非嵌入式压板同样的减约束效果。

4.2 扩口连接

扩口连接的原理如图4。

扩口连接的锥面既是密封面，又是约束面，同时限制了3个方向上的位移，并将y轴和z轴向的转动自由度也同时限制，所以是五强一弱的全约束连接，其弱约束为Rx。同整体式法兰和嵌入的压板式法兰一样，是最差的连接方式。

4.3 无扩口连接

无扩口连接的原理如图5。

单就无扩口的弹性线密封连接而言，无扩口连接允许有一定的摆动，加上管套凸肩后面的锥角，如果在安装时，尽量靠近最小拧紧力矩，无扩口连接可视为三强三弱的全约束，其强约束为Sx、Sy和Sz，弱约束为Rx、Ry和Rz。但由于飞机装配时工人操作倾向于尽可能拧紧，这种情况下两端面顶紧，所以多数情况下应视为五强一弱的全约束连接，其弱约束为Rx，也属于最差的连接方式。

4.4 球面连接

球面连接的原理如图6，包括球面连接和全球面连接2种。

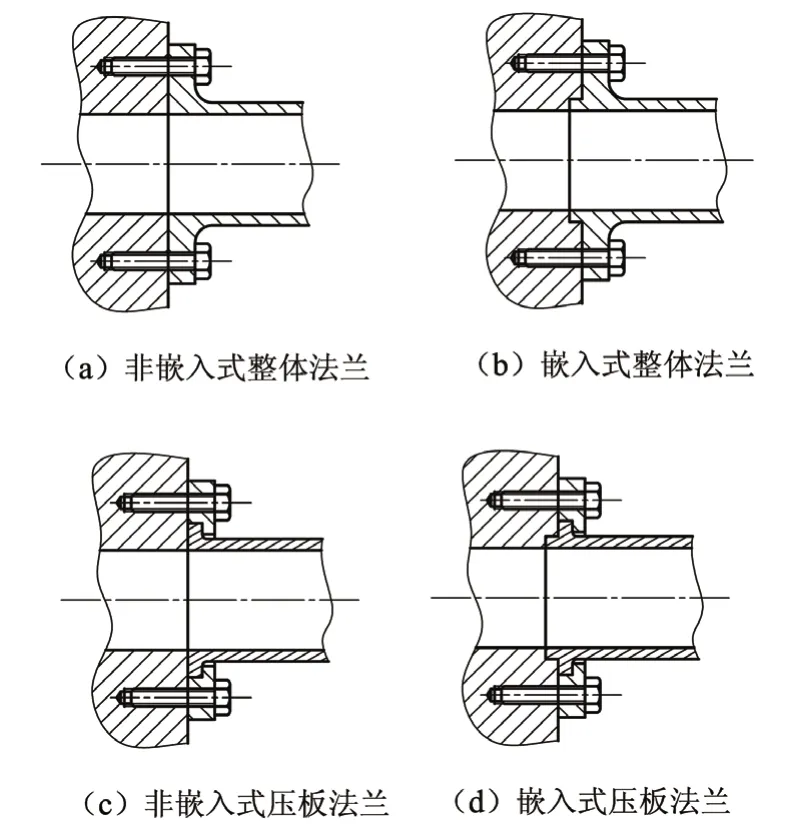
图3 法兰连接

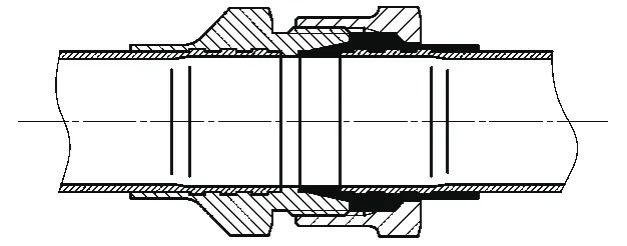
图5 无扩口连接

图6 球面连接

球面连接（图6（a））由于外套螺母在拧紧时与管嘴后端面呈强力压紧状态，因此与扩口和无扩口连接一样是五强一弱的全约束连接，其弱约束为Rx。

全球面连接（图6（b））在待拧紧状态下是3个位移约束，拧紧后，3个转动自由受到限制，形成三强三弱的全约束。其强约束为Sx、Sy和Sz，弱约束为Rx、Ry和Rz。

4.5 梁式密封连接

梁式密封连接的原理如图7。

梁式密封连接是允许在y和z轴上有一定位移自由度的，而且能允许沿y和z轴的转动，在拧紧后是一强五弱的全约束连接。其唯一的强约束是Sx，无疑是目前最好的准刚性连接形式。

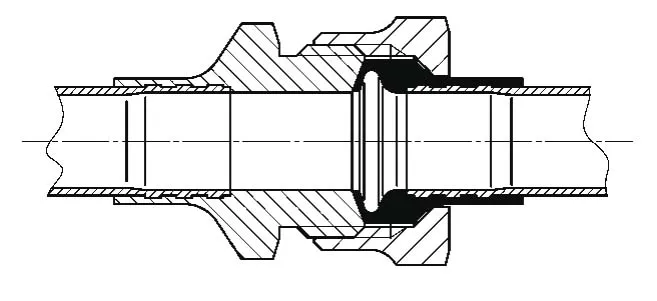
图7 梁式密封连接

4.6 柔性连接

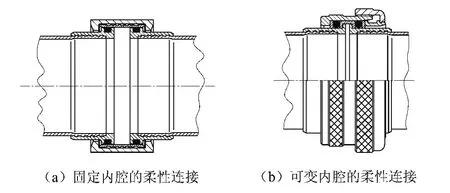
图8 柔性连接

如图8（a）和（b）。柔性连接分为固定内腔的连接和可变内腔的连接2类。从其结构上可以看出，2种连接即使是在安装状态下，也都只提供Sy和Sz两个轴向的位移约束，因此是真正的两约束连接。

4.7 插入式连接

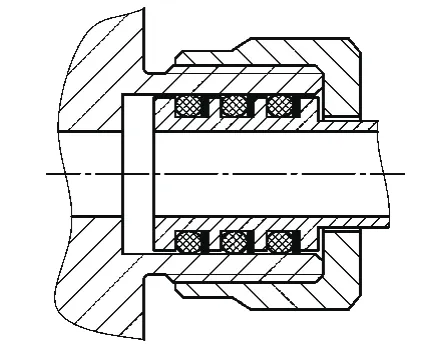
图9 插入式连接

如图9。插入式连接实际上是固定内腔柔性连接的半连接形式，所以理论上应视为Sy和Sz的两约束连接。但在实际使用中，由于工作压力比一般柔性连接高，所以密封圈的数量会随着压力的提高而增加，当只使用一个密封圈时，其约束形式与柔性连接相同，而随着密封圈数量的增加，其沿y和z的转动自由度受到越来越强的限制，因此可视为介于Sy和Sz两约束到两强两弱（强约束为Sy和Sz，弱约束为Ry和Rz。）的四约束之间。

（未完待续）