基于混合小波包的电能质量数据压缩算法

郑伟彦，吴为麟

(浙江大学电气工程学院，浙江杭州 310027）

基于混合小波包的电能质量数据压缩算法

郑伟彦，吴为麟

(浙江大学电气工程学院，浙江杭州 310027）

经典小波算法在分解电力系统监测系统的录波数据时，单一小波基难以与电能质量事件复合特征达到最优匹配，为了进一步提高电能质量数据小波压缩算法的效率，本文在单小波分解的基础上，针对电力系统数据特性提出混合小波包算法:首先通过MATLAB仿真产生不同类型的电网故障录波数据，再将仿真数据所对应的熵函数作为遗传算法寻优的代价函数，优化混合小波包基结构，最后利用新算例验证优化好的混合小波包。仿真实验的结果表明本文算法获得的压缩效果优于经典小波压缩算法。

电能质量;混合小波包;熵函数;遗传算法

现代电力系统管理和控制越来越依赖于实时监测系统的传输各个网点的录波数据。为了存储和传输海量的电网录波数据，首先要解决的问题就是研发高效的压缩算法。而电力系统数据压缩不同于其他领域的数据压缩［1］，压缩的数据必须保留故障诊断所需的扰动特征量。很多文献都采用了小波压缩算法:首先将录波信号进行小波分解，再筛选出特征系数，在保证重构波形不丢失的特征信息的前提下，要求保留的小波系数所占的存储空间必须尽可能的小。

小波变换相对于傅里叶变换的不同点在于小波分解可以根据信号特征选取不同的小波函数:选用恰当的小波函数，可以很好地分析信号的特征;相反，若小波函数选取不正确，分解系数很可能淹没信号的特征。目前经典小波中的小波空间和尺度空间是由对同一母小波函数进行伸缩，平移得到的［2］，构造起来简单，但单小波基难以与复杂数据的特征波形匹配。为此，文献［3］［4］提出了多小波电能质量压缩算法，将小波的光滑性，正交性，紧支性等完美结合起来，提高了压缩效果，但多小波计算需要对信号进行预处理，且需进行多次的小波分解构，大大增加了算法的复杂度。

为了获得多小波基的灵活性同时避免多小波计算量大的问题，文献［5］提出混合小波基的概念，并证明了混合小波基的存在。文献［6］在混合小波基的基础上提出混合小波包(Combined Wavelet Packets，CWP）。本文在此基础上优化混合小波包的算法:利用自定义的信息代价函数，通过遗传算法优化小波函数族，使得电网故障数据可以用最合适的混合小波包基来分解。与传统的小波包相比，在保持原有算法复杂度基本不变的情况下，获得更好的时频域特性和压缩性能。

1 混合小波包

1.1 小波包算法

经典小波算法具有小尺度大频窗，大尺度小频窗的时频分布规律，而电力系统中故障数据的暂态或稳态扰动通常只出现在特定频带，为了更好去除冗余，希望故障存在频带具有最大化时/频域分辨率，解决办法是在小波算法基础上推广小波包分解，使得频谱窗口进一步细化，以便找到合适的小波包树结构，用最少的小波系数提取出电力系统故障信息。

构造小波包是从长度的2N的滤波器h(n）和g(n）开始，定义函数族{wn(t）}，n=0，1，3…，当 n=0时，w0=φ(t）是尺度函数，w1=ψ(t）是小波函数，小波包WP1可以由下列递推式生成:

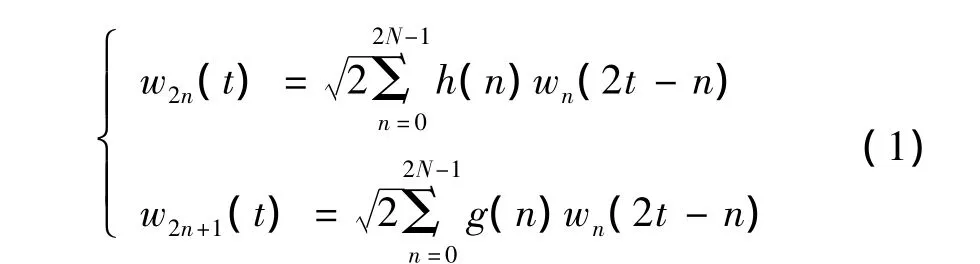
1.2 混合小波包

不同小波函数具有不同时频特性［7］:电网监测系统录波数据的低频基波部分通过高正则性，高消失矩的光滑小波基将最大部分信号能量集中;针对故障扰动，选用具有良好的时频局部性短支撑的小波基进行特征匹配，可以有效地表示系统故障的突变特征。混合的小波包可以在不同频段实现不同的小波分解，设小波函数族分别为 Ψ［1］(t），…，ψ［K］(t），对应的小波空间:({Vj}j∈z，φ［1］(t），…，{Vj}j∈z，φ［K］(t））由 k 个小波函数可以构成一组混合小波基，再由混合小波基来构造混合小波包，运用提升方案［10］构造有相同的空间结构小波包基，有φ［k］(t）∈V0⊂V1，ψ［k］(t）∈V1，k=1，2，…，K，而φ［1］(2t－n）是空间V1的正交基，所以存在∈R，∈R，使得混合小波包能够替换1.1中的小波包WP1函数形成的:

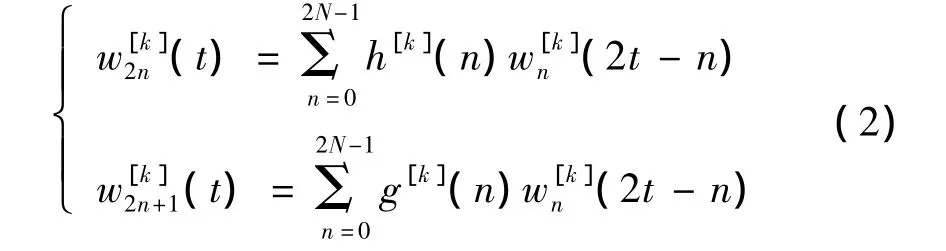
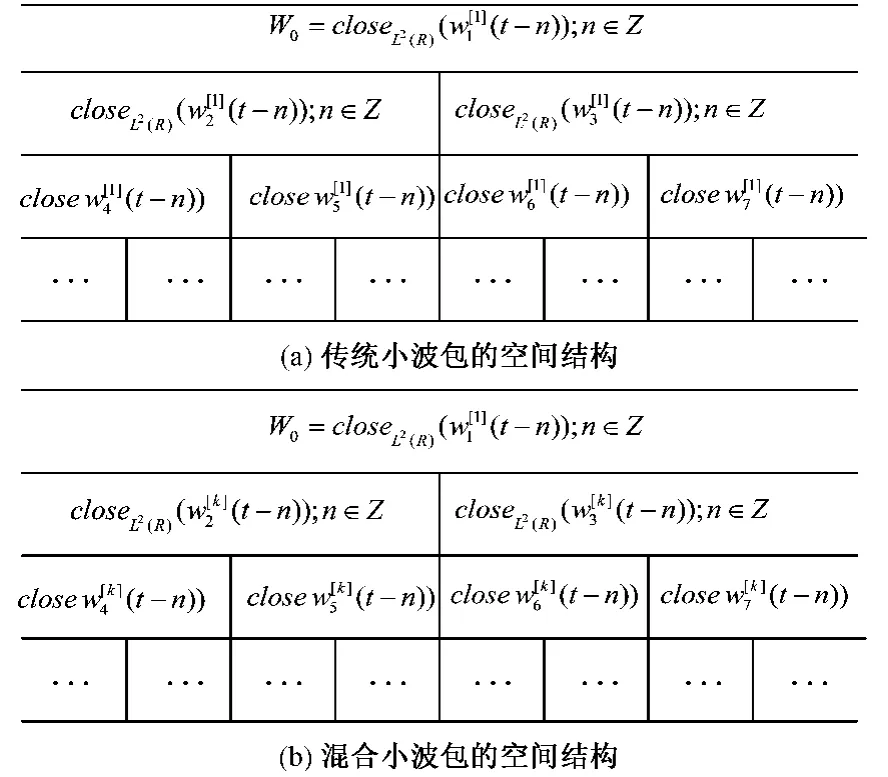
图1 混合小波包空间结构示意图Fig.1 Construction of combined wavelet packets

以电压暂降数据为算例，分别采用db1小波包，电力系统压缩最常用小波db4小波包以及混合小波包做2层分解，得到小波系数［7］，其中W20为低频系数，W21为细节系数。计算系数W21的能量集中性作为评价值1，具体原理见文献［6］，获得的数值越小表示能量越集中;计算W21系数的频带混叠性作为评价值2，具体原理见文献［9］，幅值越大表示频带混叠现象越严重。从表1可知混合小波包分解性能优于db4小波包。

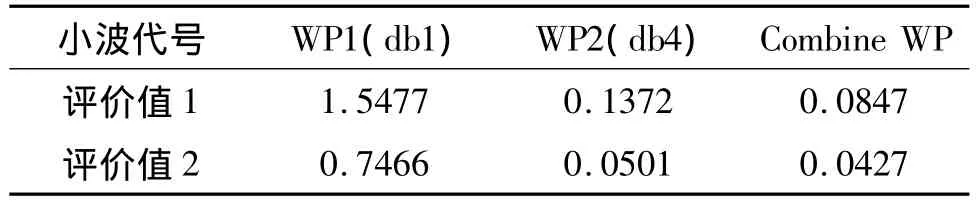
表1 传统小波包(db1 db4）和混合小波包分解效果Tab.1 Comparison between CWP and traditional wavelet

将db4和混合小波包分解的系数列出如图2，放大图2可以发现，混合小波包的对应W21中毛刺明显少于db4，说明混合小波包能量集中性好于db4小波包，更多的能量集中到低频系数W20中。

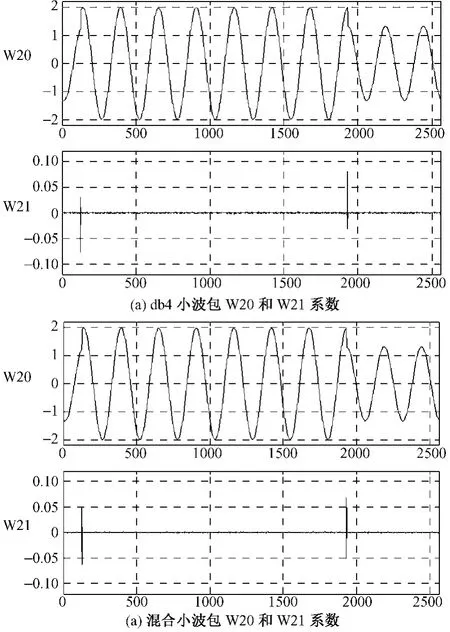
图2 传统小波包和混合小波包节点系数对比Fig.2 Coefficients of combined wavelet packets

2 优化混合小波包

2.1 基于熵准则的小波包基选择

选择小波包基的基本思想就是通过调整小波包树结构来获得最优基［9］，原始信号在小波包正交基上投影，获得一系列的系数，如果只有少数系数很大，那么用这几个少数系数就可以代表信号的特征。定义具有可加性代价函数M为代价函数。则称为M以可加性的信息代价函数。本文采用的是香农熵［7］，引入可加函数:

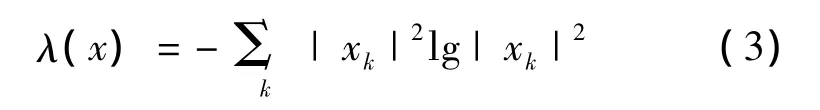
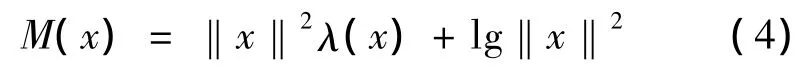
则M(x）可以表示为:将M(x）为代价信息代价的数字写在树的终端节点里。从最下层的小波包树的终端节点开始，对于非终端节点，我们采用文献［7］的步骤寻找最优树。当小波系数包含信息集中度最小时，M(x）达到最大值，反之，当信息集中度很大时M(x）对应一个极小值。因此只要计算出不同小波包基对应的M(x），具有最小M(x）值的小波包基为最优基。

2.2 遗传算法优化函数族

由上一节得到的熵函数作为遗传算法的代价函数，搜索最优小波函数族 ψ［1］(t），…，ψ［K］(t）。遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的自适应全局优化概率搜索算法［11］。它将问题的解空间组成的符号串表示为染色体，使用的遗传算子作用于染色体后进行种群繁殖，从而得到新一代种群，通过优胜劣汰完成对染色体的搜索过程。本文引入db小波，sym小波，bior小波，rbio小波，cdf小波构造混合小波函数族［13］，以3层小波包分解为例，采用6位二进制遍码构造小波函数族染色体:［w0 w1 w2 w3 w4 w5 w6 w7］，长度48位，选择方法为线性排名［11］。设定种群数量500，繁殖100代，交叉系数为250，变异系数位50，交叉算子取为整体算术交叉，变异算子采用多级变异。

按照2.1的熵函数M(x）判断染色体优劣，算法流程如下:

(a）随机初始化种群，计算M(X），保留当前最好解;(b）种群根据计算出的代价函数和选择策略确定选择概率来选择染色体;(c）根据繁殖概率和交叉系数进行繁殖或进行杂交以产生新种群。根据变异系数进行变异操作，跳出局部最优解的限制;(d）计算新种群适应值，保留当前最好解;(e）满足终止条件或迭代次数到达最大值，程序终止送出最优解;否则转到(b）。

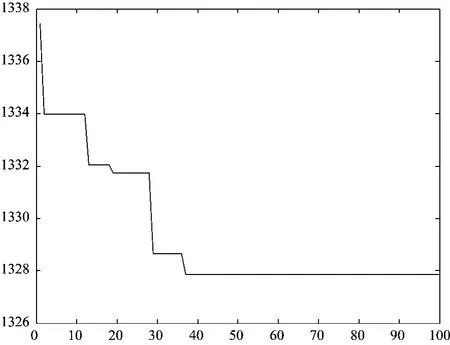
图3 遗传算法优化结果图Fig.3 Results of genetic algorithm for combined wavelet packets

图3为优化示意图:迭代40遍获得最优小波函数族。测试样本为电力系统谐波录波数据，横坐标为迭代次数，纵坐标为M(x）值。

3 基于混合小波包的压缩

为了对数据压缩算法的性能进行评估，定义了如下衡量指标［12］:

1.压缩比(CR）:

Sraw:原始数据的长度，Scmp:压缩数据的长度

2.均方误差百分值(MSE）和信噪比(SNR，db）:

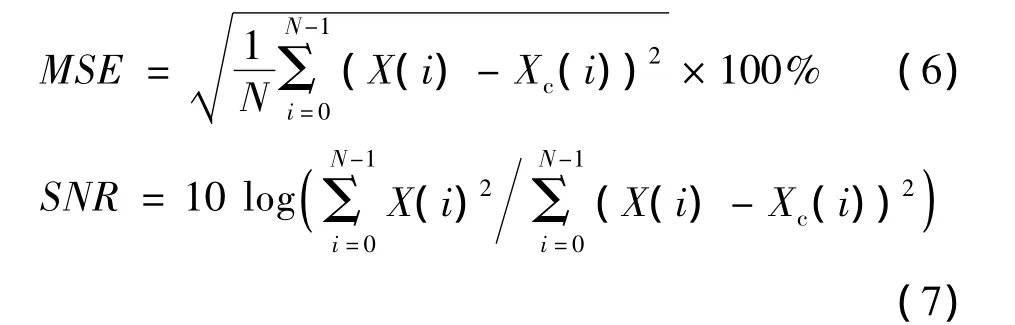
X(i）:原始的信号，Xc:(i）重建的信号，N:信号长度。

按照IEC标准测试的代表性的电能质量事件，在表2列出的暂态和稳态电能质量事件的数学模型，随机产生测试样本，持续时间为10个工频周期，实例数据采用电机启动电压电流录波数据。调整采样率12.8k，加入45db背景白噪声。

表2 电能扰动信号模型Tab.2 Disturbance signal models

4 仿真测试

采用db4小波，db4小波包以及混合小波包分别对测试样本做3层分解，为了方便对比，保留分解得到小波系数模值最大的15%用于重构信号，即在保证压缩比一定情况下，比较重构信号的精度。分别列出db4小波，db4小波包以及混合小波包压缩系数重构后与原始信号的误差指标。每种电能质量事件数据随机生成200个测试样本。表3中列出结果是200个样本的测试得到的压缩性能指标的平均值。可以看出混合小波包分解系数压缩后的恢复效果最好，小波包恢复效果略好于小波分解。

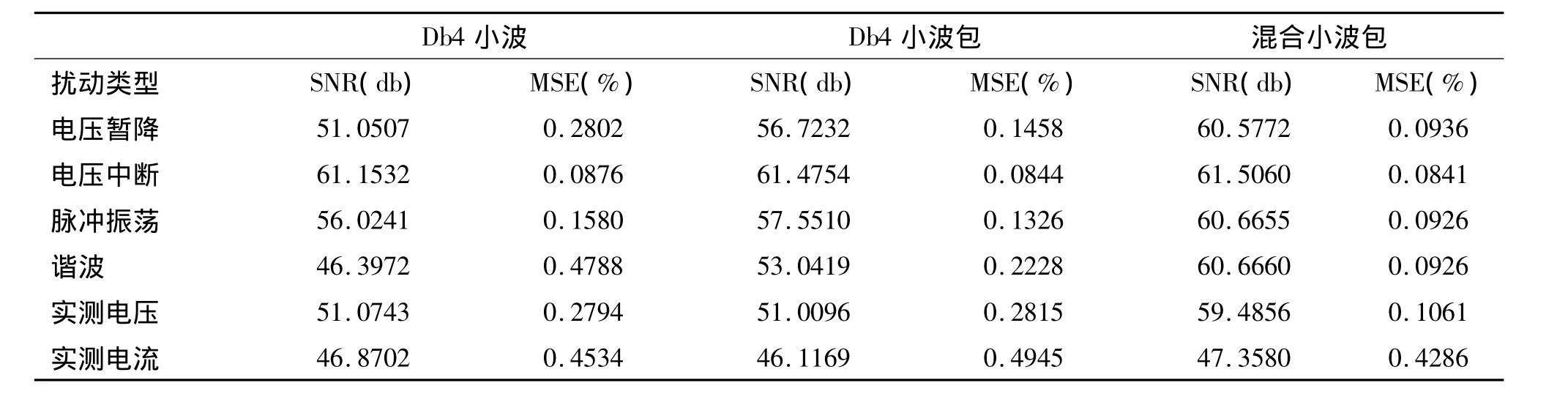
表3 电能质量数据压缩的评价指标Tab.3 Experimental results of different algorithms for PQ event data compressions

评估不同压缩算法的性能也可以在确保压缩精度一定时，比较各自的压缩比。本文采用可以良好筛选奇异信号的模极大值法［8］用于电能质量数据压缩，具体实现为:保留低频系数，对于高频系数可以计算子空间系数平均值mean和相邻的系数差值p，若(p-mean）/mean>η，η为给定阈值(本文为10）那么认为模的最大值存在，p所对应的小波系数得到保留，非模的最大值对应的系数被置零后舍弃。

分别采用模的极大值压缩脉冲振荡的小波系数。图4为压缩比CR和分解层数的关系，横坐标为压缩层数，纵坐标为压缩比。粗点划线为混合小波包压缩曲线;★号线为db4小波包压缩曲线;▲号曲线为db4小波压缩曲线。可以看出，混合小波包在不同分解层数所对应的压缩比都优于db4小波，db4小波包。

5 结论

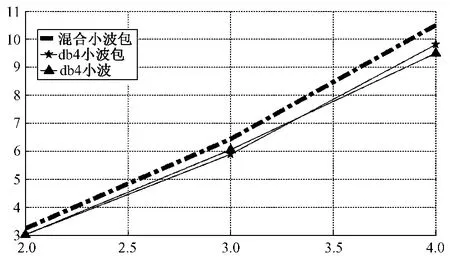
图4 分解层数和压缩比变化曲线Fig.4 Relation between CR and decomposition level

混合小波包，一种基于小波理论的创新性的电能质量压缩方法，混合多个常用，不同性质的小波基，使得小波包分解算法能够很好匹配电能质量数据的特征，达到减少有效分解系数的效果，并通过遗传算法优化，得到混合小波包的最佳频域分辨率和最佳小波函数族，对于电能质量事件数据的压缩性能优于传统小波/小波包变换。

References）:

［1］Robertson D C，Camps O I.Wavelets and electromagnetic power system transients［J］.IEEE Trans.on Power Delivery，1996，11(2）:1050-1058.

［2］Stéphane G Mallat.A wavelet tour of signal processing［M］New York:Academic Press，1999.

［3］Mariantonia Cotronei，Laura B Montefusco，Luigia Puccio.Multiwavelet analysis and signal processing ［J］.IEEE Trans.on Circuits and Systems—II:Analog and digital signal processing，1998，45(8）:970-987.

［4］刘志刚，钱清泉 (Liu Zhigang，Qian Qingquan）.基于多小波的电力系统故障暂态数据压缩研究(Compression of fault transient data in electric power system based on multiwavelet）［J］.中国电机工程学报 (Proc.CSEE），2003，23(10）:22-26.

［5］Chen Yuyu，Zhang Bo.Band-limited combined orthogonal wavelet bases［A］Australia IEEE TENCON’1996［C］.New York:Academic Press，1996.593-597.

［6］陈玉宇，张钹(Chen Yuyu，Zhang Bo）.混合小波包与最佳基 (Combined wavelet packets and best base）［J］.软件学报 (J Software），1998，9(3）:161-168.

［7］The MathWorks，Inc.Matlab 2007b Help Document［Z］.2007.

［8］刘应梅，白晓民，易俗，等 (Liu Yingmei，Bai Xiaomin，Yi Su，et al.）.基于最小极大法的电力扰动信号压缩(Compression of power system disturbance signals based on least maximum method）［J］.电网技术 (Power System Tech.），2004，28(3）:33-37.

［9］Coifman R R，Wickerhauser M V.Entropy based algorithms for best basis selection［J］.IEEE Trans.on Information Theory，1992，38(2）:7l3-718.

［10］Daubechies，W Sweldens.Factoring wavelet transforms into lifting steps［J］.The Journal of Fourier Analysis and Applications，1996，4(3）:247-269.

［11］潘正君，康立山，陈毓屏 (Pan Zhengjun，Kang Lishan，Chen Yuping）.演化计算 (Evolutionary computation）［M］.北京:清华大学出版社(Beijing:TUP），1998.

［12］Salomon David.Data compression［M］Publishing House of Electronics Industry，2003.

［13］Pascal Getreuer.Filter coefficients to popular wavelets［OL］.http://scholar.google.cn，May 2006.

［14］陶顺，肖湘宁 (Tao Shun，Xiao Xiangning）.基于短板效应的电能质量综合等级评价(Synthetic grading evaluation of power quality based on incentive mechanism）［J］.电工电能新技术 (Adv.Tech.of Elec.Eng.＆Energy），2008，27(2）:16-20.

A power quality event data compression based on combined wavelet packets

ZHENG Wei-yan，WU Wei-lin
(College of Electrical Engineering，Zhejiang University，Hangzhou 310027，China）

As the time-frequency characteristic of single wavelet base cannot match with complex signal feature，the compression effect could hardly be improved further in wavelet compression method，so this paper proposed combined wavelet packets based on wavelet packets algorithm for power quality signal compression.For different kinds of power quality data we using genetic algorithm search for the optimal combined wavelet packets base assemblage by using wavelet entropy function as cost function.The simulation results show that new algorithm gets better results when compare to the traditional wavelet and wavelet packet method at the same conditions.

power quality;combined wavelet packets;entropy function;genetic algorithm

TM769

A

1003-3076(2010）03-0008-04

2009-11-15

郑伟彦(1981-），男，福建籍，博士研究生，从事电能质量数据分析和挖掘研究;

吴为麟(1944-），男，浙江籍，教授/博导，研究方向:电能质量、电力电子在电力系统中的应用。

book=21,ebook=11