基于减基法的有阻尼结构谐响应快速分析方法

黄 芬 韩 旭 黄永辉

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082 2.中联重工科技股份有限公司,长沙,410013

0 引言

结构谐响应分析是结构分析很重要的一方面,它可以确保一个给定的结构能经受住各种不同频率的正弦载荷,有助于结构设计人员掌握结构的持续动力特性,并在必要时避免或利用共振。结构谐响应分析需要求解大型多自由度系统方程,这个循环求解的过程非常耗时。目前有许多降阶方法可用来解决这类问题,如Guyan静力凝聚法[1-2]、动力子结构法[3]等,但这些方法在提高效率和保持原模型的物理特性上仍存在一定的局限性,即使是降阶后,求解仍比较耗时。

减基法[4-5]是20世纪70年代提出的一种降阶方法。其基本思想是,当系统由多个参数描述时,这些参数的不同组合会使系统方程有不同的解,而系统在新参数下的解可以由事先设计的样本参数组所对应解的线性组合来得到。近年来,不少学者对该方法进行了研究。国外,Maday等[6]从理论上证明了减基法的一致指数收敛性质;Rovas[7]把减基法应用于不同种类偏微分方程的求解中;国内,减基法在结构动力学中的应用研究处于起步阶段,文献[8]引入减基法,在波数域内快速分析了复合材料层合板的瞬态响应问题。李永红等[9]将减基法用于结构特征值分析与参数优化中,求解了无阻尼结构的固有频率与振型。黄永辉等[10]通过减基法在实数范围内分析了无阻尼结构的谐响应问题。然而,在目前可查资料中,尚未见减基法用于有阻尼结构谐响应分析的报导。

本文在有阻尼的线弹性结构谐响应分析中引入减基法,在离散化的频域中进行对数预采样[8],求出样本点的解向量,得到一系列的复数解向量。而无阻尼的结构谐响应分析得到的样本点的解向量是一系列的实数解向量,后续工作都是在实数域中进行的。有阻尼的情况要考虑直接用复数解向量或是向量的模来构造减基空间。复数向量包含幅值和相位两个属性,用模来构造减基空间,把复数域的工作转换到实数域进行,会丢失向量的相位属性,因而考虑直接利用复数解向量,通过贪婪算法[6]构造减基空间,把系统的刚度矩阵、质量矩阵、阻尼矩阵以及载荷列向量分别投影到减基空间进行降阶,得到减缩系统。在减基空间求解原问题的减缩解,并把减缩解还原到原空间得到原问题的近似解。通过误差和计算耗时的对比,验证了这种方法在有阻尼的结构谐响应分析中的可靠性和有效性。

1 有阻尼结构谐响应分析的有限元形式

谐响应分析是用来计算结构在简谐载荷激励下响应的方法。在谐响应分析中,激励外载是已知的,可以是力也可以是位移、速度或加速度。

在谐响应分析中,激励载荷在本质上为正弦载荷,在最简单的情况下,这种载荷可通过特定频率下的幅值来定义。简谐响应与载荷以相同的频率出现,由于系统阻尼的影响,响应在时间上可能移位,响应移位也称相位移位,因为载荷峰值与响应峰值不是同时出现的。

在谐响应分析中,一般有两种不同的数值方法可供选择：直接法和模态法。直接法根据外载荷频率求解耦合的运动方程;模态法利用结构的振型缩减和解耦运动方程,对各个模态响应进行叠加得到一特定外载荷频率的解。

简谐载荷作用下的有阻尼结构的运动方程为

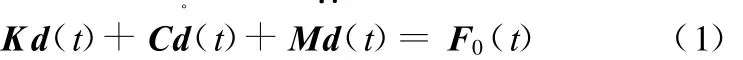
其中,F0(t)为简谐激励载荷,F0(t)=F(ω)eiωt;F为载荷幅值;ω为激励载荷的频率,当载荷幅值不变时,F与 ω无关,可写成F0(t)=F eiωt的形式。K、M、C分别为结构的整体刚度矩阵、质量矩阵和分别为结构的整体位移向量、速度向量、加速度向量。对于简谐运动,假设一个简谐形式的解：

式中,d0(ω)为复位移向量。

将式(2)代入式(1)并化简得

当考虑阻尼时,式(3)代表复系数方程系统。当激励频率范围较大时,式(3)的求解次数也随着增多,反复求解工作量大。另一方面,当系统自由度n很大时,求式(3)非常耗时,需要考虑计算成本问题。

在实际问题中,要精确地计算结构受到的阻尼是很困难的。通常从整体上考虑阻尼的影响,近似地估计阻尼力做功消耗的能量。一般有限元程序中,假定整体阻尼矩阵C是整体刚度矩阵K与整体质量矩阵M的线性组合,成为Rayleigh阻尼(或比例阻尼),其表达式为

其中,Ω为结构固有频率;ξ为阻尼比;比例系数α、β可通过测试结构自由振动的衰减率经过换算得到。当阻尼比ξ确定时,α、β也可通过式(5)得到。

2 有阻尼结构的减基法谐响应分析

减基法用于结构谐响应分析的目的是缩减刚度矩阵、质量矩阵和阻尼矩阵的阶数,同时保证减缩后的系统能很好地近似原系统,以提高求解效率。计算过程分为离线和在线两阶段。

2.1 离线阶段

结构谐响应分析的主要变化参数是载荷频率ω。本文将频域离散成m个频率点,对频率点进行预采样,目前预采样方法有对数采样法、等间隔均匀采样法、Chebychev采样方法等。本文用对数采样方法采取N个样本点,采样公式如下：

式中,λ为常数;μj为采样参数的值;μmax为采样参数的最大值。

N＜m时,初步构造频率的样本空间如下：

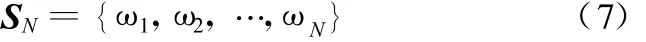
在每一个样本点求式(3),由于本文考虑的是有阻尼的系统,式(3)中存在复数项,所以得到的N个解向量也是复向量,样本点的复数解向量构成解空间如下：

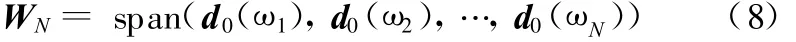
将d0(ω)分离成与变化参数有关部分 α(ω)和无关部分D,则有

那么式(3)可写成

式中,α为原系统在减基空间的减缩解。

两边乘以DT得

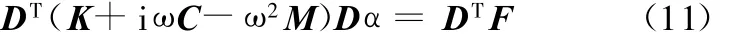
当D为n ×N1阶正交矩阵时,称K N1、C N1、M N1、F N1分别为K、C、M、F关于D的正交投影,且K、M、C、F的阶数由n×n变成N 1×N1,当K N1=DTKD,CN1=DTCD,MN1=DTMD,FN1=DTF,N1＜n时,矩阵得到降阶。

为了得到正交矩阵D,构造减基空间,本文引入贪婪算法,对解空间WN进行自适应训练。这个过程中,与无阻尼情况的区别是,样本点的解向量都是复数向量,构成的空间也是复空间,贪婪算法是在复数域进行的。为了保证解向量的正交性,同时避免减缩矩阵的病态问题,每将一个解向量加入减基空间,就要采用施密特正交化方法对减基空间的向量进行正交归一化。贪婪算法的具体步骤如下：

(1)从预采样点的解空间中选择一个解向量加入减基空间。

(2)当构造减基空间的向量个数大于1时,用施密特正交化方法把解向量正交归一化,构造新的减基空间,并得到正交矩阵D。

(3)通过伽辽金映射将与参数 ω无关的K、M、C、F矩阵投影到减基空间,得到缩减后的矩阵和系统控制方程,在预采样点进行求解,得到 N个解向量。

4.假设该化妆品使用的税率如下：进口关税税率=t，消费税率=c,增值税率=ν。根据《关于跨境电子商务零售进口税收政策的通知》，计算可得：

(4)利用2范数,求N个样本点的减基误差和投影误差。减基误差向量e r的第j个分量定义为

投影误差向量e p的第j个分量定义为

式中,d0j为直接求解的第j个样本点的解向量;αj为减基空间中的第j个样本点的解向量。

(5)判断最大减基误差是否小于给定的误差限ε,若满足,停止贪婪算法;若不满足,将最大投影误差对应的预采样点的解向量放入减基空间,重复步骤(2)～步骤(4)。

通过贪婪算法构造的减基空间能很好地近似原来的空间,可表示为

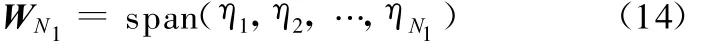
式中,ηi(i=1,2,…,N1)为构成减基空间的样本点的解向量。

且一般情况下N1＜N。

2.2 在线阶段

利用正交矩阵D将K、M、C、F降阶得减缩矩阵 K N1、C N1、M N1、F N1。

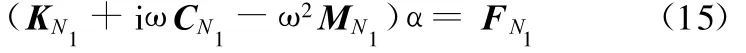
由于减基空间中的各个向量线性无关,故这些向量可以作为任意参数下解空间中N 1维子空间的基,则原系统的解向量可以用减基空间解向量的线性叠加来近似：

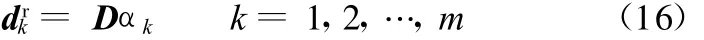
3 减基法与直接法之间的误差

为了验证减基法的有效性,需要定义减基法求解与直接求解之间的误差,利用欧几里德范数定义相对误差：

其中,d0k为直接求解式(3)得到的解向量,根据数值分析中方程组近似解可靠性判别法[11],可利用系数矩阵条件数以及残余向量来判断减基法得到的近似解是否可靠。令

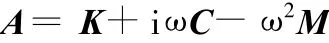
当

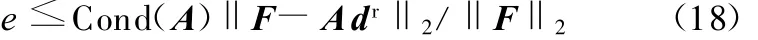
时,近似解是可靠的。其中,Cond(*)为求矩阵A条件数的函数。

4 算例

算例一 以一L形振动试验夹具为例,材料常数如下：弹性模量 E=70GPa,泊松比μ=0.33,密度ρ=2.8×103kg/m3,夹具板厚度0.01m。该夹具通过4个螺栓连接在振动平台台面上,其几何结构尺寸及螺栓位置如图1所示,有限元模型如图2所示,共有791个节点、2373个自由度,在747节点y方向施加简谐载荷,幅值1000N,频率3500～4500Hz,系统受瑞利阻尼作用,阻尼比ξ=0.05。

将频域离散成200个子步,用对数预采样采集31个频率点,给定的减基误差限ε1=1×10-5,经过贪婪算法,最终选出7个点即可满足精度要求。减基法把原来2373×2373的系数矩阵缩减为7×7的矩阵,大幅度提高了求解效率。计算用MATLAB程序实现,在CPU主频为2.01GHz、内存为1GB的电脑上运行,直接求解与减基法方法求解时间对比见表1。减基法求解所耗时间几乎是直接求解的1/5,效率明显提高。

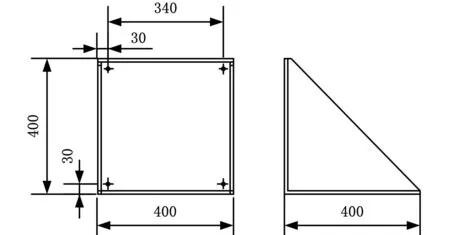
图 1 夹具几何尺寸(单位：mm)

图2 夹具有限元模型

贪婪算法过程中,减基误差、投影误差分别如图3、图4所示,减基误差从第1代到第2代迅速减小,随后逐渐收敛于误差限10-5。投影误差变化趋势与减基误差基本相同,第3代后缓慢收敛,继续增加基数量对误差影响不大,以减基误差判断,当基数量达到7时,误差小于给定误差限。

图3 减基误差随着基向量个数增加的变化情况

相对误差如图5所示,其中最大相对误差为3.73×10-11,满足式(18),图6给出了减基法求解与直接求解得到的响应幅值,找到一频率在4000Hz附近的共振点,两种所得结果一致,说明减基法能得到高精度的解,且所耗时间比直接求解所耗时间少。

图4 投影误差随着基向量个数增加的变化情况

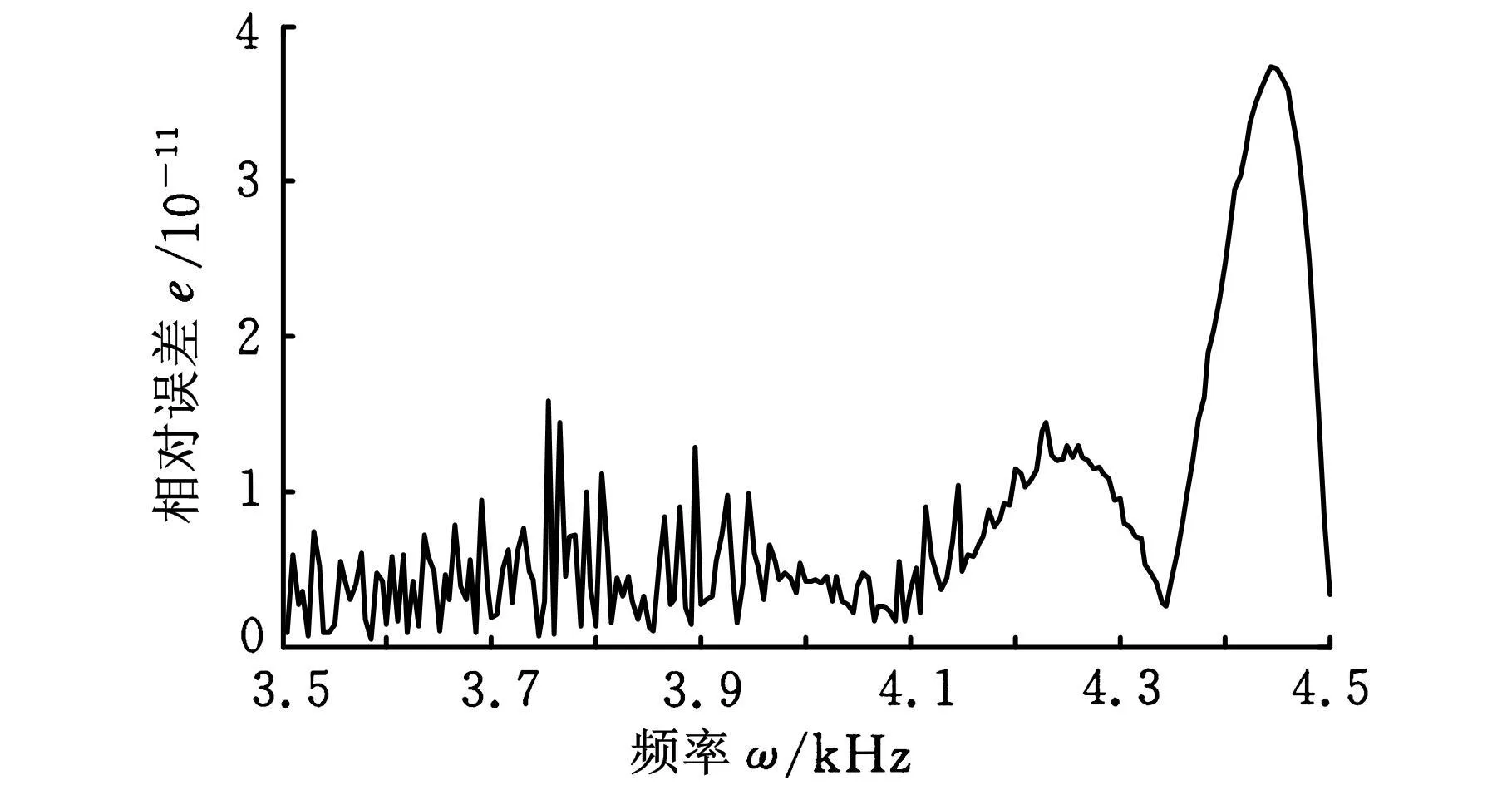
图5 减基法求解与直接求解之间的相对误差

图6 减基法与原方法的响应幅值比较(701节点y方向)

算例二 考虑如图7所示的板梁支架结构,梁底端固支,弹性模量E=200GPa,泊松比μ=0.3,密度 ρ=7.8×103kg/m3,板长 0.8m,宽0.4m,厚 0.01m。梁截面为实心,宽0.03m,高0.04m。支架的每段支撑高0.4m。有限元模型如图7所示,共有405个节点、2430个自由度,分别在支架的219节点、270节点、347节点加载z方向同频率简谐载荷,幅值分别为1000N、750N、500N,频率为0～300Hz,同样受瑞利阻尼作用,阻尼比ξ=0.06。

与算例一同理,在离散为300个子域的频域中采取16个点,贪婪算法选出10个点即可满足精度要求,本例减基误差限ε=1×10-3,两种方法耗时如表2所示。减基误差、投影误差的变化如图8、图9所示,趋势基本相同,从第 1代到第7代迅速减小,随后逐渐收敛于误差限10-2。当基数量达到11时,误差小于给定误差限,此时,构造的减基空间满足精度要求,减缩系统的刚度矩阵、质量矩阵、阻尼矩阵阶次由 2430×2430降到11×11。

图7 支架结构有限元模型

表2 减基法求解和直接求解的时间对比

图8 减基误差随着基向量个数增加的变化情况

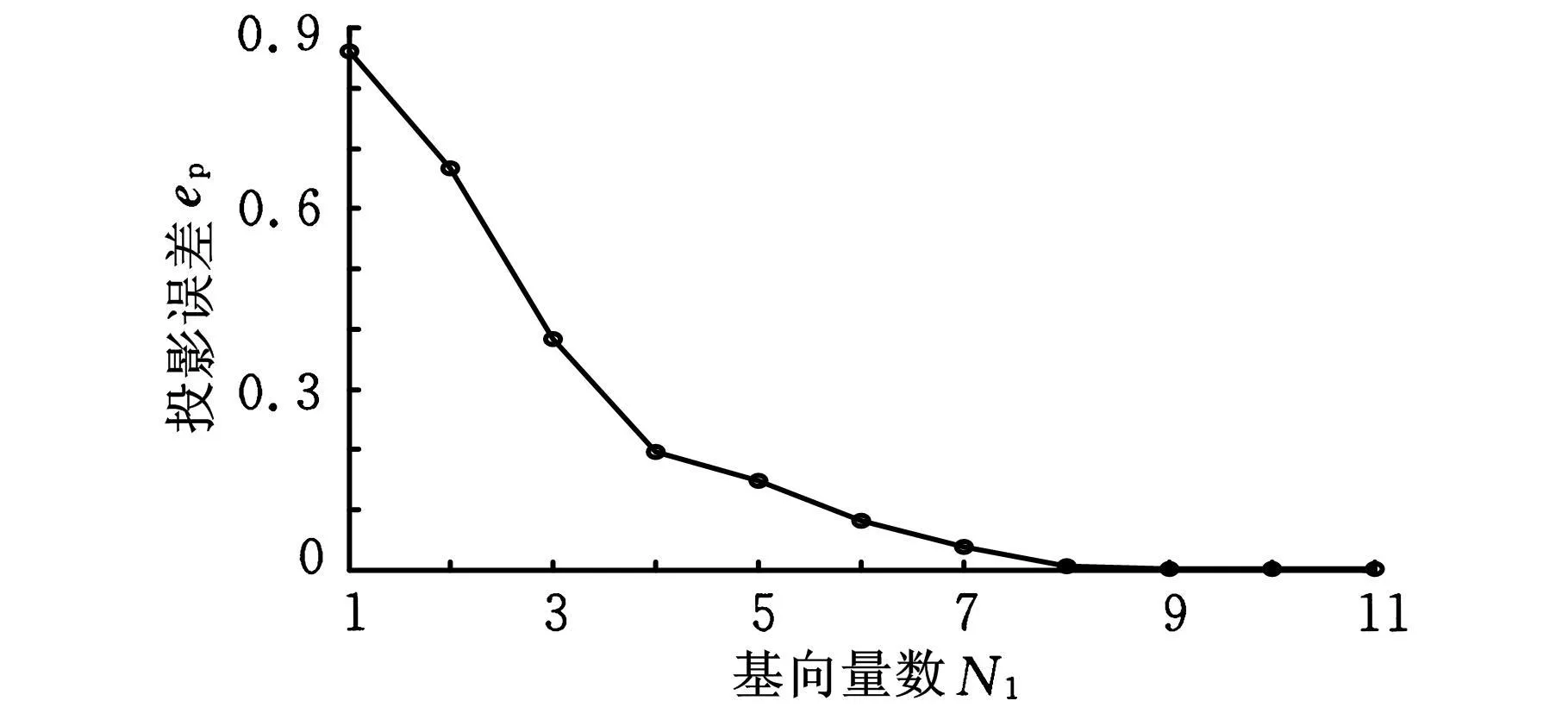
图9 投影误差随着基向量个数增加的变化情况

最后的相对误差如图10所示,其中最大误差为1.01×10-5,满足式(18),同时由表2知,减基法耗时只是直接求解耗时的1/7。图11给出了减基法与直接法求解的响应幅值,实线为有限元法直接求解的结果,点线为减基法求解结果,由图11可见减基法与原有限元法的结果一致,通过曲线找到共振点频率约为80Hz。

以上两个算例说明在有阻尼的线弹性结构谐响应分析中,利用减基法求解可以明显提高效率,并保证解的精度,最大误差均满足误差限,说明减基法和原方法的结果是可靠的,也说明了该方法的有效性。

5 结束语

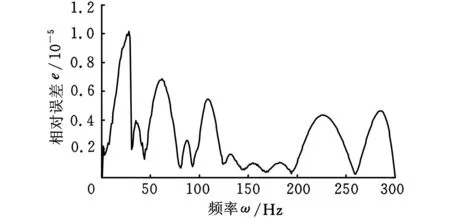
图10 减基法求解与直接求解之间的相对误差

图11 减基法与原方法的响应幅值比较(86节点 x方向)

本文在有限元的基础上,把减基法用于有阻尼的线弹性结构谐响应分析。分析过程中,把简谐载荷频率离散,通过对数预采样和贪婪算法构造减基空间,把原系统映射到减基空间进行降阶,在很大程度上缩减了系统刚度矩阵、质量矩阵、阻尼矩阵的阶数,从而节省了求解资源,有效提高效率。本文算例表明,减基法在解决无阻尼的结构谐响应分析的基础上,同样适用于有阻尼的结构谐响应分析。

[1] Gu J.Efficient Model Reduction Methods for Structural Dynamics Analyses[D].Michigan：The University of Michigan,2000.

[2] Guyan R J.Reduction of Stiffness and Mass Matrices[J].AIAA Joumal,1965,3(2)：380-381.

[3] Wilson E L,Yuan M W,Dickens J M.Dynamic Analysis by Direct Superposition of Ritz Vectors[J].Earthquake Engineering Structural Dynamics,2006,10(6)：813-821.

[4] Noor A K,Peters JM.Reduced Basis Technique for Nonlinear Analysis of Structures[J].AIAA Journal,1980,18(4)：455-462.

[5] Veroy K,Patera A T.Certified Real-time Solution of the Parameterized Steady Incompressible Navier-Stokes Equations：Rigorous Reduced-basis a Posteriori Error Bounds[J].International Journal for Numerical Method in Fluids,2005,47(8/9)：773-788.

[6] Maday Y,Patera A T,Turinici G.A Priori Convergence Theory for Reduced–basis Approximations of Single-parameter Elliptic Partial Differential E-quations[J].Journal of Scientific Computing,2002,17(1/4)：437-446.

[7] Rovas DV.Reduced-basis Output Bound Methods for Parametrized Partial Differential Equations[D].Cambridge：Massachusetts Institute of Technology,2002.

[8] 黄永辉,韩旭,冉承新.基于减基法的层合板瞬态响应快速分析方法[J].力学学报,2008,40(2)：255-260.

[9] 李永红,李光耀.Reduced-basis Method在特征值问题中的应用[J].机械制造,2008,46(525)：5-9.

[10] 黄永辉,韩旭,黄芬.基于减基法的结构谐响应快速分析方法[J].振动与冲击,2009,28(7)：61-64.

[11] Gerald C F,Wheatley PO.应用数值分析[M].北京：机械工业出版社,2006.

[12] 马超,吕震宙.结构可靠性分析的支持向量机分类迭代算法[J].中国机械工程,2007,18(7)：816-819.

[13] 许兆堂,朱如鹏.阻尼分段阶梯传动轴主共振的分析[J].中国机械工程,2006,17(7)：685-690.