低承台小群桩共同作用诱发变形特征

陈乐求，杨恒山

(湖南理工学院 土木建筑工程学院，湖南 岳阳，414006)

桩基础是应用广泛的一种基础形式[1]，随着现代化城市向着平面和空间迅速发展，城市土地日益紧张，基础选型往往存在一定局限，此时，桩基础就显示出其优于其他基础形式的特性[2]。近年来，随着工业建设的发展，在我国的大中型城市建设中涌现出一大批多层(4～9层)大柱距、大开间的工业厂房和仓储超市商业网点，单柱荷载非常大(常为5～10 MN)，若要设计为整板基础，则底板厚度非常大，柱间、板内局部弯矩和局部剪力也很大，其造价相对于整个建筑的造价来说太大，因此，通常设计为柱下扩展基础。当承载力不够时，柱下常设计为低承台小群桩的群台基础。低承台小群桩可充分发挥地基土的承载能力，满足荷载及变形条件，降低工程造价[3-7]。目前，在设计时往往只考虑群桩的承载力问题，而较少考虑台与台之间的变形差问题，忽视了台间不均匀沉降对结构物应力的影响，一旦结构梁出现开裂，不了解不均匀沉降的影响程度[8]。由于低承台群桩基础的承载力非常大，无法通过原型载荷试验来研究和确定承载能力和相应沉降，因此，采用数值模拟分析方法研究群桩基础的工作性能具有重要的理论意义和实际意义[9]。在此，本文作者采用古典弹性理论计算法，对桩、土位移方程进行部分改进，使其计算精度提高，并用 Digital Visual Fortran语言编制计算程序，研究低承台小群桩在考虑桩-土-承台共同作用下荷载与变形的关系，以便为该类建筑物的设计与施工提供参考。

1 计算方法

对基于弹性理论法的桩、土位移方程进行改进，通过推导极限积分公式，采用辛普森梯形积分法进行数值积分，所得计算结果精度比以往采用矩形积分法所得精度更高。

1.1 单桩计算公式

1.1.1 土的位移方程

对于均质半无限空间中长度为L的桩，将桩均匀划分成n个单元，所有单元上作用的剪应力p及桩底均布压力pb在计算点产生的位移之和为：

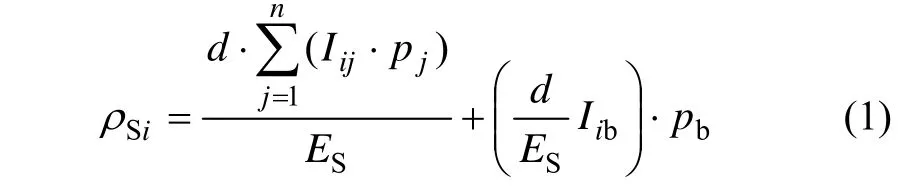
式中：pj为任意单元 j上作用的均布剪应力；pb为桩底均布压力；Iij为单元j上的剪应力在i单元中点桩土界面处产生的垂直位移因子，用弹性半空间的Mindlin解计算[10]；d为桩径；ES为土的弹性模量；Iib为桩底均布压力在i单元中点桩土界面处产生的铅直位移因子。

对桩底也可写出类似的方程。因此，桩侧土总的位移方程为：

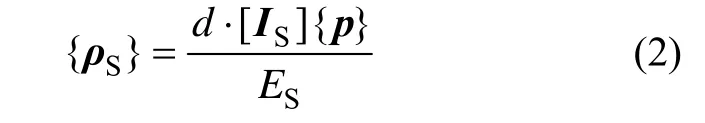
式中：}{Sρ为土的位移列阵，n+l阶；{p}为桩周及桩底荷载列阵，n+1阶； ][SI 为(n+1)×(n+1)阶土的位移系数方阵。

[IS]中的元素由Mindlin方程积分求取。

1.1.2 桩的位移方程

式中：}{Pρ为n+l阶桩位移列阵；[IP]为(n+1)×(n+1)阶桩的位移矩阵；EP为桩弹性模量；RA为桩面积与桩周边界的面积比；nL/=δ为单元长度。

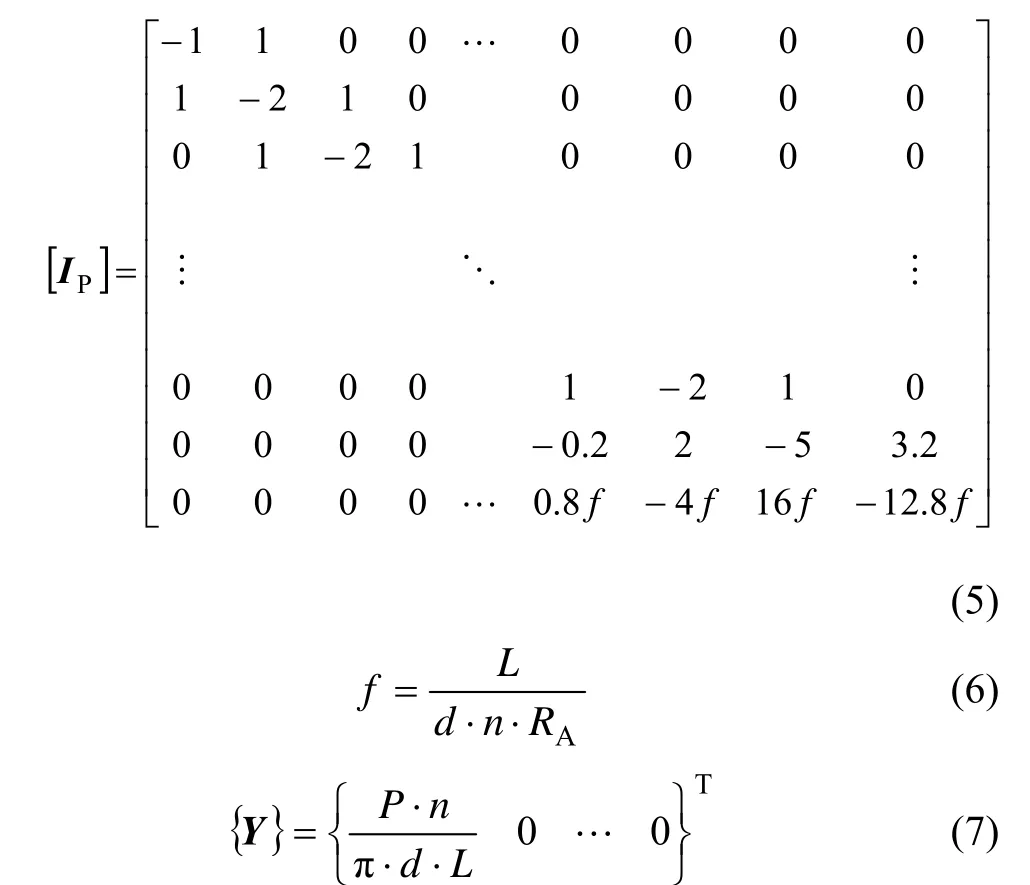
其中：L为桩长；P为荷载。

1.1.3 桩-土位移相容性

1.2 低承台小群桩计算公式

对于低承台，承台与地面有效接触，除了桩间土分担一定的荷载之外，承台压力会增加铅直向应力，进而增加极限桩侧摩阻力和极限桩端阻力，即所谓“增强效应”。由于承台限制了浅层桩、土相对位移，因此减小了部分极限桩侧摩阻力，即存在“削弱效应”。对于这些“效应”，采用如下处理方法：承台压力在某桩的某一单元产生的位移因子，采用地面荷载面积积分的方法，用矩形面积上的积分减去各桩圆面积上的积分。桩顶圆面积上的均布荷载在i桩某一单元上的位移因子为[11]：

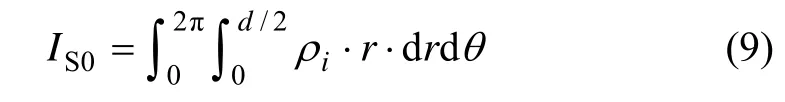
式中：iρ仍为Mindlin方程，其对半径r的积分为

r的积分范围为0～d/2，θ的积分范围为0～π2。对θ的积分不能写成显式，仍需用数值积分。积分后，数值要除以桩径 d，以便成为无量刚单位用于土的位移方程。

对于低承台小群桩，考虑承台影响的桩侧土位移方程为：

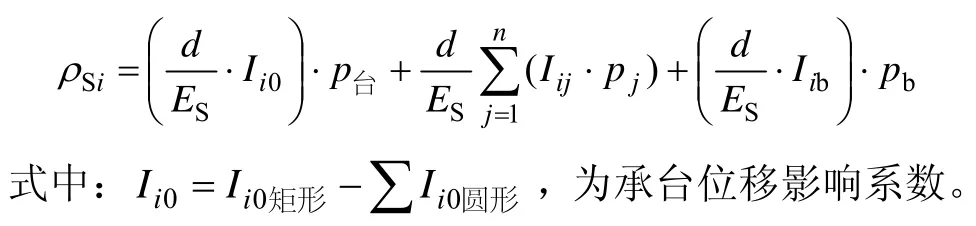
图1 低承台小群桩荷载-沉降计算程序框图Fig.1 Flow chart of load-settlement calculating procedure of low-cap group piles

2 程序设计

基于上述计算公式，用Digital Visual Fortran语言编写了计算低承台小群桩沉降曲线的程序，其程序框图如图1所示。由于承台底压力与承台沉降相关，均匀分布的承台底压力只能对应相同的桩顶沉降，因此，计算中采用“各桩桩顶沉降相同”的计算模式。

在每一级荷载下，首先计算不考虑承台作用且各桩沉降相同条件下群桩的沉降及各桩的沿桩长接触应力的分布；将桩顶沉降代入承台底基床系数即可计算得到承台底压力；得出各桩沿桩长接触应力和承台底压力后，用考虑承台底压力的土位移方程计算桩侧土各单元的位移，与该情况下桩的各单元位移(在考虑台底压力使桩侧摩阻力与桩端阻力增大的情况下)进行比较。若第1单元土位移大于桩位移，则说明承台底土压力大(桩承担荷载比例小)，因此，需减小承台底基床系数直到桩土位移协调为止；若桩位移大于土位移，则说明桩土已发生滑动，桩土位移不再协调，因此，只需考虑承台底压力所起的分担荷载、增加极限侧摩阻力与极限桩端阻力的作用。

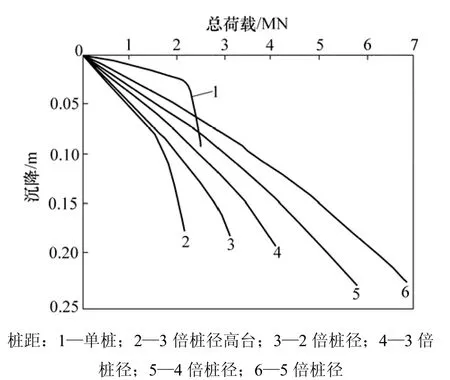
图2 不同桩距基桩荷载-沉降曲线比较Fig.2 Comparison of pile load-settlement curves for different pile spacings

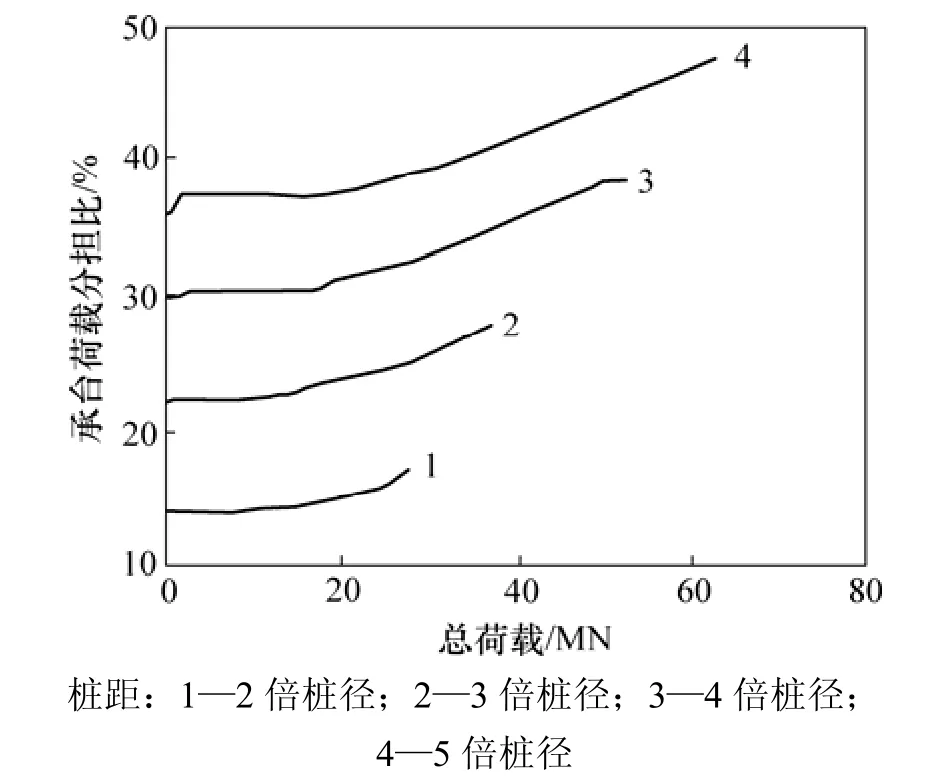
图3 不同桩距的承台荷载分担比变化情况Fig.3 Development process of cap load sharing ratio for different pile spacings

3 共同作用诱发变形特征

3.1 桩和土的参数取值

根据有关工程经验，钢筋混凝土桩的弹性模量取值为：EP=2.3×104MPa。土的弹性模量根据土质不同，可以在5.5～62.5 MPa之间，本次计算取ES= 9 MPa。

研究表明：桩的荷载-沉降关系对桩的泊松比µ不敏感[12]，因此，计算中取中密土的经验值，即35.0=µ。

3.2 不同桩距对荷载-沉降曲线的影响

为了比较桩径、桩长、桩距、承台底基床系数对低承台小群桩荷载-沉降关系的影响，仍以 9桩小群桩为主要研究对象，分析桩径分别为0.4，0.6和0.8 m，桩距分别为2倍桩径、3倍桩径、4倍桩径、5倍桩径，桩长分别为5，10，20和30 m，承台底基床系数分别为0.75，1.50，3.00和4.50 MPa/m时的荷载-沉降关系及承台荷载分担比随总荷载增长的变化，结果分别见图2～3。分析桩数对荷载-沉降关系影响时，采用2根桩、3根桩、4根桩的情况。

图2所示为桩径0.8 m、桩长20 m、承台底基床系数为1.5 MPa/m，不同桩距时低承台基桩的荷载-沉降曲线，对应的承台荷载分担比变化见图3。图2中同时绘制了高承台、桩距为 3倍桩径时的基桩荷载-沉降曲线和单桩的荷载-沉降曲线。由图 2可知：低承台小群桩(基桩)的荷载-沉降曲线与单桩及高承台群桩(基桩)的荷载-沉降曲线均有较大差别。

3.2.1 基桩的平均承载力受桩-土-承台共载影响特征

由图2可知：当高承台小群桩中桩距为3倍桩径时，基桩平均临塑承载力比单桩的平均临塑承载力小约30%；而承台底基床系数为1.5 MPa/m的低承台桩基，在桩距为2倍桩径时，群桩中基桩的临塑承载力已超过单桩的极限承载力；随着桩距的增加，基桩的承载力达到单桩极限承载力的2倍以上，而承台荷载分担比不到总荷载的30%(见图3)；当桩距为5倍桩径时，虽然承台荷载分担比由稳定段的36%发展到后期的47%，但对应的基桩承载力达到单桩极限承载力的3倍，即由于台底压力的作用，不仅承台分担了部分荷载，桩本身所能承担的荷载也大大提高。

3.2.2 总体沉降受桩-土-承台共载影响特征

由图 2可知：与高承台小群桩的荷载-沉降曲线相比，低承台小群桩荷载-沉降曲线前部直线段沉降减少主要是承台分担荷载作用产生的，增大的桩侧摩阻力和桩端阻力还未起作用，因而沉降相差不大；在荷载作用后期，当高承台桩基的沉降量急剧增大时，荷载接近并超过临塑荷载，低承台桩基的荷载-沉降曲线刚刚处于缓变阶段；其后，低承台群桩的承载能力可能增大，而高承台群桩桩周与桩底均发生剪切破坏。

3.2.3 桩-土-承台共同作用下承载力提高对总体沉降的影响

由图2可知：桩-土-承台共同作用使群桩中的基桩承载力远远大于单桩承载力，但其对应的群桩桩台沉降比单桩的临塑荷载对应的沉降要大得多，即使在5倍桩径桩距时，同样荷载对应的沉降量比小桩距时的沉降量小很多，但在基桩受荷量与单桩临塑荷载相同时，对应的沉降量比单根桩临塑荷载作用下的沉降量大1倍。因此，要发挥桩-土-承台共同作用增大的承载力是有前提条件的，即上部结构要允许有较大的沉降量[13]。

3.3 不同承台底基床系数对荷载-沉降曲线的影响

图4所示是桩径为0.6 m、桩距为3倍桩径，桩长为20 m时不同承台底基床系数对应的小群桩荷载-沉降曲线，与其对应的承台荷载分担比变化见图 5。由图4可知：当承台底基床系数增加时，群桩的承载力增加(相应的基桩承载力也增加)，且群桩的荷载-沉降曲线转折减缓。至承台底基床系数增加至3.0 MPa/m时，荷载-沉降曲线几乎变为1条直线。由图5可知：随着承台底基床系数增加，承台的荷载分担比也相应增加，且承台荷载分担比有所变化；当台底基床系数较小时，承台荷载分担比在一个稳定段后有一个急升段，与群桩荷载-沉降曲线转折后的沉降快速增长段相对应；而当台底基床系数较大时，承台荷载分担比曲线转折减小，且稳定增长段延长。

3.4 不同桩长对荷载-沉降曲线的影响

不同桩长时基桩荷载-沉降曲线见图6，与其对应的承台荷载分担比见图7。由图6可知：当桩距、承台底基床系数相同时，桩长增加，群桩中基桩承载力增加，荷载-沉降曲线趋缓。由图 7可知：承台荷载分担比变化规律也有所不同，当桩长较短时，荷载分担比稳定段较短，且分担比增长段斜率很大；而当桩长较长时，荷载分担比稳定段较长，且分担比增长段很平缓(斜率很小)。

图4 不同承台底基床系数的荷载-沉降曲线比较Fig.4 Relationship between load and settlement for different coefficients of subgrade reactions

图5 不同承台底基床系数的承台荷载分担比Fig.5 Development process of cap load sharing ratio for different coefficients of subgrade reactions

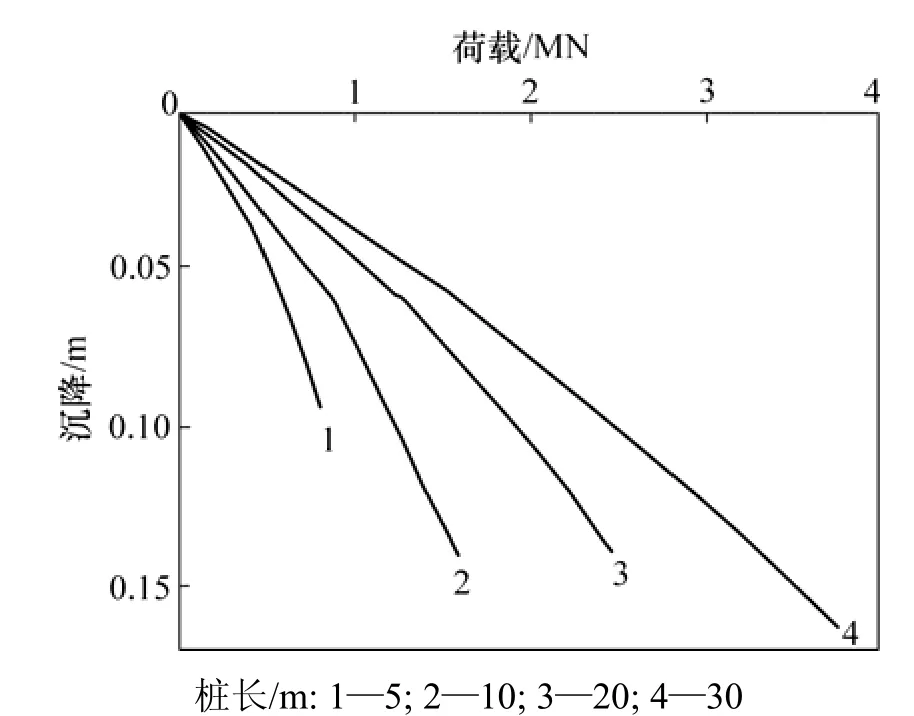
图6 不同桩长时基桩荷载-沉降曲线比较Fig.6 Comparison of pile load-settlement curve for different pile lengths

图7 不同桩长时的承台荷载分担比的变化情况Fig.7 Development process of cap load sharing ratio for different pile lengths

3.5 不同桩径对荷载-沉降曲线的影响

图8 所示是9根桩、桩距为2.4 m、桩长为20 m、承台底基床系数为1.5 MPa/m时，桩径分别为0.6 m与0.8 m的群桩总荷载-沉降曲线的比较结果，2种情况下的承台面积相当。由图8可知：在桩台面积、承台底基床系数相同时，桩径增加，群桩承载力提高，基桩承载力相应提高，荷载-沉降曲线变缓，即桩径增加，承载力提高[14]，但同时对应沉降也较大。

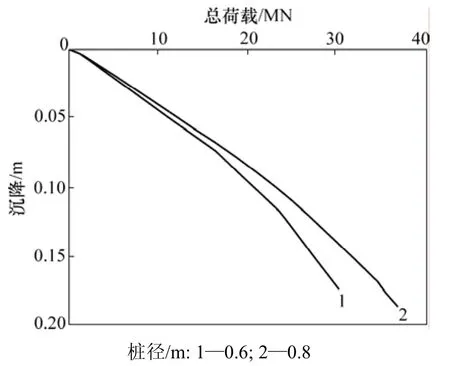
图8 不同桩径荷载-沉降曲线比较Fig.8 Relationship between load and settlement for different pile diameters

3.6 不同桩数对荷载-沉降曲线的影响

图9 所示是桩径为0.4 m、桩距为1.2 m(即3倍桩直径)、桩长为20 m、承台底基床系数为1.5 MPa/m、桩数不同时总荷载-沉降曲线的比较结果。2根桩并排排列，承台为矩形；三根桩呈正三角形排列，承台为三角形；四桩呈正方形排列，承台为方形。为进一步分析，将群桩荷载除以桩数，换算成基桩荷载-沉降曲线，见图10，与两图对应的承台荷载分担比见图11。由图10和图11可知：在低承台情况下，当各桩对应承台面积不变时，桩数增加，不仅群桩承载力增加，群桩中基桩的承载力也有所增加，这与通常的“群桩中单桩发挥作用要折减”的观点是相反的。其原因是：在同样荷载下，基桩(群桩)的沉降有所增加，这样，不仅承台分担荷载增加(见图 11)，增加的台底压力使桩侧极限摩阻力与桩端阻力也有所增加，因而基桩的承载力增加。由图11可知：当桩数不同时，承台荷载分担比曲线形态相似，桩数较多的群桩其承台荷载分担比也较大。

由图10可知：当桩群总体受荷相同时，桩数较多的群桩其沉降较小，但在基桩受荷相同时，桩数较多的群桩其沉降量增加。若以单桩载荷试验测得的沉降量(如10 mm)来控制，则各桩的承载力远远不够。因此，当结构物不同部位产生的荷载不同时，提高桩的数量虽能提高承载力，但沉降量不一定满足设计要求。

图9 不同桩数的群桩荷载-沉降曲线比较Fig.9 Comparison of group pile load-settlement curves for different pile numbers

图10 不同桩数基桩荷载-沉降曲线比较Fig.10 Relationship between load and settlement for different pile numbers

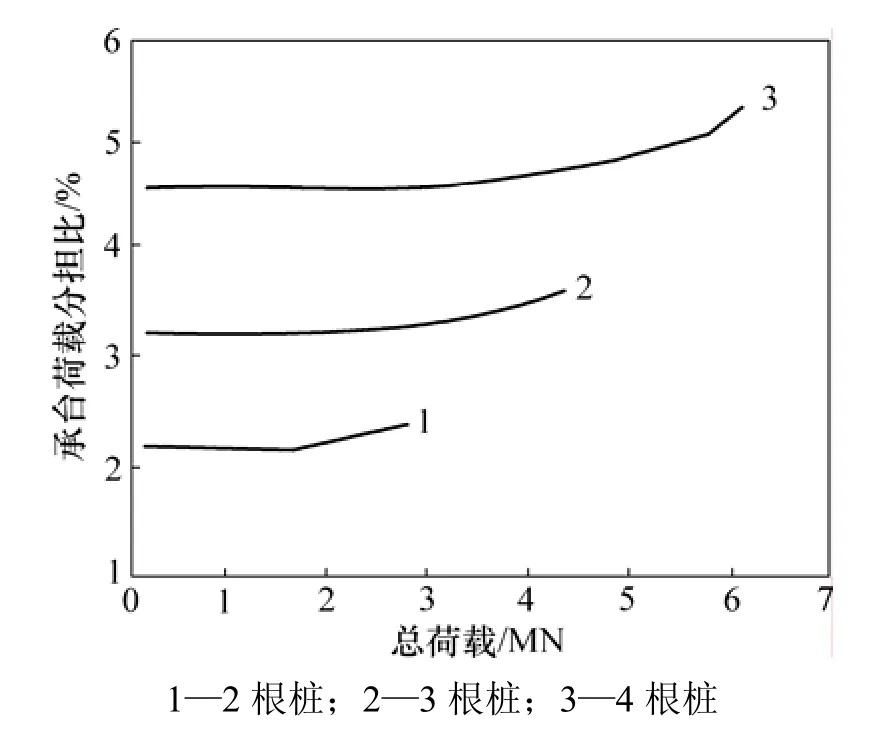
图11 不同桩数承台荷分担比的变化情况Fig.11 Development process of cap load sharing ratio for different pile numbers

综上所述，低承台小群桩的荷载-沉降曲线基本上呈缓变状态。在达到极限荷载之前，荷载-沉降曲线只有很小的转折，若荷载增量稍大，则显示不出转折部分，但荷载并不是可以无限增加的[15-16]。低承台小群桩的受荷变形受桩距、桩径、桩长、桩数、承台尺寸、承台底基床系数等多种因素的影响。

4 结论

(1) 基于弹性理论法对桩、土位移方程进行了改进。通过推导极限积分公式，采用辛普森梯形积分法进行数值积分，比以往的矩形积分法所得结果精度更高。

(2) 用Digital Visual Fortran语言编写了分析低承台小群桩变形特征的程序，并得到了不同条件下低承台小群桩的荷载-沉降曲线，为低承台小群桩的进一步研究提供了思路。

(3) 低承台小群桩的荷载-沉降关系呈缓变特征。基桩承载力及沉降均比单桩的大，随着桩长、桩径、承台底基床系数的提高，群桩承载力及基桩承载力相应提高，但同时沉降也较大，桩端阻力在总承载力中所占比例较小，因而，低承台小群桩的临塑荷载与极限荷载相差很小。桩数增加，群桩承载力及基桩承载力相应增加，当桩群总体受荷相同时，桩数较多，则其群桩的沉降较小；在基桩受荷相同时，桩数较多，则其群桩的沉降增加。

(4) 低承台小群桩的受荷变形特征与单桩及高承台群桩的受荷变形特征明显不同。低承台小群桩的受荷变形受桩距、桩径、桩长、桩数、承台尺寸、承台底基床系数等多种因素的影响，进行工程设计时，要综合考虑这些因素，以达到最佳效果。

[1] 桩基工程手册编写委员会. 桩基工程手册[M]. 北京: 中国建筑工业出版社, 1995: 1-5.

The Committee of Pile Engineering Handbook. Pile engineering handbook[M]. Beijing: China Architecture & Building Press,1995: 1-5.

[2] 申兆武. 超高层建筑桩筏基础的理论分析和工程应用研究[D].上海: 同济大学土木工程学院, 2008: 2-15.

SHEN Zhao-wu. Research on super high-rise building pile-raft foundation’s theory and application in engineering[D]. Shanghai:School of Civil Engineering. Tongji University, 2008: 2-15.

[3] 王浩, 周健, 邓志辉. 桩—土—承台共同作用的模型试验研究[J]. 岩土工程学报, 2006, 28(10): 1253-1258.

WANG Hao, ZHOU Jian, DENG Zhi-hui. Model tests on pile-soil-cap interaction[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1253-1258.

[4] Poulos H G, Davis E H. Pile foundation analysis and design[M].New York: John Wiley & Sons, 1980: 28-40.

[5] Cooke R W. Piled raft foundation on stiff clays: A contribution to design philosophy[J]. Geotechnique, 1986, 36(2): 169-203.

[6] Poulos H G. Piled raft foundations: Design and application[J].Geotechnique, 2001, 51(2): 95-113.

[7] 宰金珉. 塑性支承桩-卸荷减沉桩的概念及其工程应用[J]. 岩土工程学报, 2001, 23(3): 273-278.

ZAI Jin-min. Concept of plastically bearing pile and its practical application[J]. Chinese Journal of Geotechnical Engineering,2001, 23(3): 273-278.

[8] 温特科恩. 基础工程手册[M]. 方晓阳, 译. 北京: 中国建筑工业出版社, 1983: 103-108.

Winterkorn H F. The foundation engineering handbook[M].FANG Xiao-yang, trans. Beijing: China Architecture& Building Press, 1983: 103-108.

[9] 王幼青, 衣北宇. 低承台群桩基础工作性能数值模拟研究[J].黑龙江大学自然科学学报, 2006, 23(2): 147-150.

WANG You-qing, YI Bei-yu. Numeric simulation research on bearing capacity behavior of low cap pile group foundation[J].Journal of Natural Science of Heilongjiang University, 2006,23(2): 147-150.

[10] 董建国, 赵锡宏. 高层建筑地基基础—共同作用理论与实践[M]. 上海: 同济大学出版社, 1997: 279-300.

DONG Jian-guo, ZHAO Xi-hong. Ground foundation of high-rise building: Theory and practice of joint-action[M].Shanghai: Tongji University Press, 1997: 279-300.

[11] 刘金砺. 桩基础设计与计算[M]. 北京: 中国建筑工业出版社,1994: 106-142.

LIU Jin-li. Design and calculation of pile foundation[M]. Beijing:China Architecture & Building Press, 1994: 106-142.

[12] 楼晓明, 刘建航, 洪毓康. 两个相邻高层建筑桩箱基础的共同作用分析[J]. 土木工程学报, 2002, 35(3): 55-60.

LOU Xiao-ming, LIU Jian-hang, HONG Yu-kang. Study on interaction of two adjacent pile-box foundations[J]. China Civil Engineering Journal, 2002, 35(3): 55-60.

[13] 吴兴序. 桩的端阻和侧阻相互作用及其工程应用价值[J]. 西南交通大学学报, 1997, 32(3): 313-318.

WU Xing-xu. Interactions between friction and tip resistance of piles and their significance in construction[J]. Journal of Southwest Jiaotong University, 1997, 32(3): 313-318.

[14] 李发明, 陈竹昌, 刘利民. 桩侧阻力的几种退化效应简述[J].土工基础, 1998, 12(1): 41-46.

LI Fa-ming, CHEN Zhu-chang, LIU Li-min. Several kinds of deterioration of side resistance of single pile[J]. Soil Engineering and Foundation, 1998, 12(1): 41-46.

[15] 刘金砺. 桩基研究与应用若干进展浅析[J]. 岩土工程界,2000(2): 10-14.

LIU Jin-li. Simple explanation on the advances of research and application of pile foundation[J]. Geotechnical Engineering World, 2000(2): 10-14.

[16] Mylomlds G, Gazetas G. Settlement and additional internal forces of grouped piles in layered soil[J]. Geotechnique, 1998,48(1): 55.