隧洞内构造形迹产状数学模型解析

2010-05-31杨凤宝卢长伟宋宝玉

东北水利水电 2010年2期

杨凤宝，卢长伟，宋宝玉

（吉林省水利水电勘测设计研究院，吉林长春 130012）

洞探是水利水电工程地质勘察中最重要的勘察手段之一。平洞对于准确查明岩性界线，尤其是沉积岩岩性界线及构造带 (以下统称构造形迹)至关重要。平洞内构造形迹的准确量测，对于工程项目中地质剖面图的精确绘制及平面图中构造迹线的绘制是最为有效的方法，其位置及规模的精确查明，对于工程选址及建筑物的优化布置及工程处理方案起着决定性作用。目前对于洞内构造迹线的量测，根据构造本身规则程度、洞径大小及施工成洞爆破工艺所影响的洞臂光滑程度，主要有以下两种量测方法。

直接量测法。主要适用于构造出露迹线比较规则，且成洞较差，有足够大的构造面可以直接用罗盘量测。

支杆量测法。主要适用于洞径较小(一般小于5m)、爆破工艺较高，洞臂较光滑，没有足够大的构造面可以直接用罗盘量测，则可以用1根可以伸缩的塔尺直抵两洞臂同一高程上构造出露位置，用罗盘量测直尺方向即为构造形迹走向。走向±90°即为倾向，其倾角的量测可以用2根可以伸缩的塔尺，分别抵至两洞臂该构造形迹2个不同高程处，用另外1根尺子垂直两平行塔尺，量测该尺子倾角即为该构造形迹倾角。该方法较准确，但较麻烦，遇到洞径较大时量测很不方便，难度大。

当遇到洞径较大(一般大于5m)时，尤其是爆破工艺较高，洞臂较光滑，没有足够大的构造面可以直接用罗盘量测时，或构造形迹不是很规则时，以上两种方法均显得力不从心。此时准确量测该构造总体产状显得难度极大，有些工程技术人员采取了大致的量测方法，此是对工程不负责任、对科学极不严谨的态度，是不可取的。针对此问题，认真的分析研究了构造形迹产状的定义，并在工程实践过程中不断的归纳，总结出了在该工况条件下计算构造形迹产状的数学模型。

1 数学模型理论基础

任何理论的发现与发展都离不开最基本的公理与定义，都是在此基础上的进一步拓展，隧洞内构造形迹产状数学模型也不例外，该数学模型的理论基础就是构造地质学中对构造产状的定义。

（1）走向。是构造面与水平面相交的线的延展方向，走向线就是构造面上的水平线，即构造面上同一高程两点的线的延展方向。

（2）倾向。构造面上垂直于岩层走向并向下倾覆的方向。

（3）倾角(真倾角)。构造面与水平面所夹的最大角度，即垂直于走向方向的夹角。

在以上定义及空间三角几何图形概念的基础上，总结出了隧洞内构造形迹的产状计算数学模型。

2 数学模型的基础资料

隧洞内构造形迹产状计算数学模型，需要有一张精确度高的隧洞展示图。要求在做隧洞展示图时采用测量仪器或罗盘准确量测出隧洞的前进方向及洞顶底板、洞臂相应高程，准确量测出构造形迹在两洞臂及洞顶的出露位置，并将其如实的绘制在隧洞展示图相应的位置上。此为隧洞内构造形迹产状数学模型最重要的第一手基础资料。

3 计算数学模型

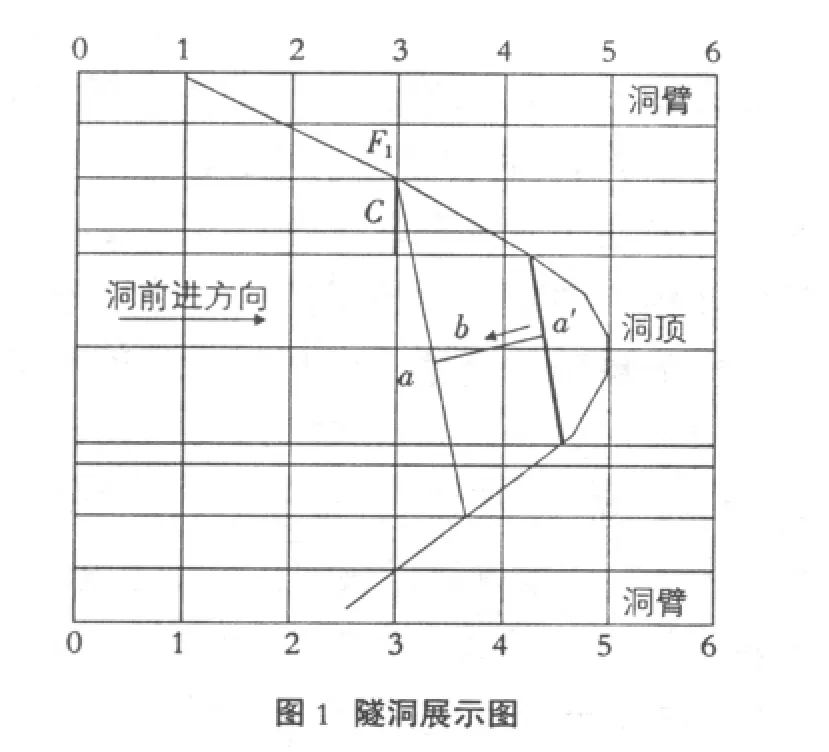
图1 隧洞展示图

如图1中：F1为云南省宣威市万家口子水电站工程坝址区中左岸平洞PD1中的一个断层，找出F1断层与两洞臂与洞顶交汇处出露点 (位于同一高程)，并将其连线，再在左右两洞臂同一高程处找到F1断层的出露点，并将其连线，如图1中a，其两侧延伸方向即为该断层的走向线。图中其它线段及符号意义如下：

a，a′为该断层走向线；数值可以根据其与隧洞前进方向的夹角确定，a，a′为任意两个构造形迹上高程相同的点的线；b为方向为倾向，长度为两走向线间的水平距离，可以从图中根据隧洞前进方向读或量取；c为两走向线间高差，可以从图1中读或量取。

4 计算数学模型工程实践检测

根据以上总结出的隧洞内构造产状数学模型，对云南省宣威市万家口子水电站坝址区的10个平硐精确地绘制了展示图，选择了构造面在洞内出露较好的构造形迹共12条，进行了实地量测并与数学模型计算出的产状进行对比，对比结果完全吻合。根据以上数学模型结论及检测结果，对平硐内构造面出露不完整、量测准确度低的构造形迹全部采用该数学模型，又进行了室内计算进行统计，最终在勘察成果的应用上以室内计算产状为依据，并于2005年7月份该勘察成果通过云南省专家审查认可。