基于序列响应面方法的高强度钢材料参数反求

张 勇 陆 勇

华侨大学，厦门，361021

0 引言

汽车碰撞安全性是汽车设计过程中主要考虑的因素之一［1］，随着计算机硬件技术及数值仿真技术的快速发展，基于数值仿真技术的汽车安全性设计正逐渐替代传统的物理整车碰撞安全性实验。但是，整车碰撞安全性的仿真精度在很大程度上取决于所选材料的本构方程，而本构方程中的材料参数，如弹性模量、硬化指数、应变率、应变速度导致的温度效应等将直接影响到仿真结果的精确性［2］，因此，准确获得材料参数对提高碰撞安全仿真结果的可靠性有着显著的科学意义和实际应用价值。

此外，准静态工况下进行的单向拉伸试验得到的材料参数，往往难于反映材料在大变形、大应变、材料快速变形过程中的发热等对材料性能的影响。材料参数的诸多不确定性使得碰撞安全性仿真的结果时常与实验结果具有较大的误差。因此，本文采用有限元技术与数值优化相结合的方法来反求材料的各类参数。该方法采用优化方法进行迭代寻优，从而调整实验曲线点与仿真曲线点的逼近程度。但是对于碰撞安全这类涉及大位移、大变形的高度非线性仿真问题，当数值优化方法需要成千次调用正问题的计算时，计算成本将成几何级数的增长，导致优化设计不可行，此外，基于整个设计空间构造的近似模型的精度常常较低，导致基于该模型的优化解的精度差，且不易找到全局最优点［3］。因此，笔者采用逐次逼近的序列响应面方法，使其能在较小的设计空间中构建出高精度的近似模型，从而较好地解决上述问题。

基于物理实验与数值仿真的几何与材料参数的识别研究，已取得一些成果［4－13］，但是，基于近似模型方法的材料参数反求，特别对于高强度钢板DP800的材料参数反求的文献仍然鲜有报道。因此，笔者将序列响应面近似模型方法与小种群遗传算法相结合，在基于DP800制作的薄壁吸能管碰撞试验数据的基础上，基于真实的试验条件建立了相关的有限元仿真模型，从而来开展针对高强度钢板DP800的各项材料性能参数的反求。

1 序列响应面方法

1.1 响应面模型的构建

响应面方法是一种将试验设计与数理统计相结合来建立经验模型的一种优化方法［3－4］，它采用拟合与插值的方法分析试验设计点，从而构建出目标函数与约束函数的响应面近似模型，并以该模型来替代物理有限元模型进行寻优并预测非试验设计点的响应值。

实际应用过程中，一般采用二阶多项式响应面模型，其函数关系为

式中，j为设计变量的个数；β0、βi、βii、βil为待定系数。

当选取了n个试验设计点时，响应面函数可以通过矩阵形式表示为

式中，ε为误差矢量。

回归系数β采用最小二乘拟合方法确定，即

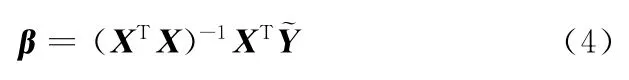
1.2 响应面模型的更新与逐次逼近

设计空间的大小对响应面近似模型的精度具有重要的影响，本文采用在优化过程的不同阶段逐步更新与缩放设计空间的方法，使优化设计问题的求解域从初始设计空间中一个较大的设计域转化成一个较小的信赖域。与在整个设计空间构建的近似模型相比，较小的信赖域内构建的近似模型的精度更高。

设经过第k次优化设计后，设计空间将变为第k＋1次信赖域，而第k＋1次信赖域的中心即为第k次信赖域中的优化设计点x［k］，此次信赖域的缩放和移动关系可用下式表示［3］：

为了保证信赖域更新过程中各变量的缩放比例保持一致，取λ作为所有变量的部分因子，也称之为变换因子，其表达式为

此时，第i个设计变量在第k＋1次设计子空间的上下界为

在优化设计过程中，整个信赖域的移动和缩放如图1所示。

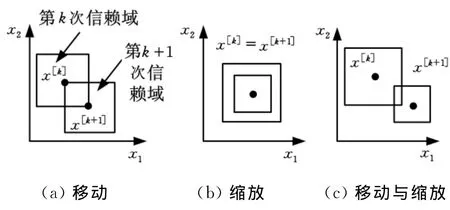
图1 信赖域的变化示意图

通过设计空间的逐步移动和缩放，优化问题将收敛在一个较小的信赖域中进行，得到精度较高的响应面近似模型与最优设计点，该方法能够有效地消除噪声，改善优化算法的收敛性能。

1.3 D最优试验设计

在整个设计空间选取有限数量的样本点，使之尽可能地反映设计空间的特性，即称为试验设计。试验设计是构建近似模型的基础，设计样本点的选取是否合适对后续的响应面近似模型的构建起着非常重要的作用，它将直接影响构建的近似模型的精度，故试验设计方法的选取也显得尤为重要。因此，如何在设计空间内最优布置试验设计点，也是当前试验设计理论研究的热点之一。本文采用了Draper等［14］提出的D最优试验设计方法来获取采样点。

2 DP800高强度钢材料参数的反求

2.1 DP800薄壁吸能梁的试验与反求仿真模型

薄壁吸能梁的碰撞试验示意图以及它的几何截面参数分别如图2与图3所示。其中，试件夹持在夹具中，其夹持长度L2＝100mm，碰撞吸能自由端的长度L1＝310mm，碰撞质量台车的质量为600kg，它以15m／s的速度正面碰撞DP800吸能梁，碰撞过程中通过力与加速度传感器采集碰撞力与减速度［4］。

图3中，薄壁梁的截面宽度b1＝60mm，截面高度b2＝60mm，界面的圆角半径R1＝3mm，R2＝2mm，其帽形梁的焊接法兰长度为25mm，高强度钢板DP800的板料厚度为1.2mm。碰撞试验后得到的碰撞力及其变形量等相关试验数据源于参考文献［4］。

图2 薄壁梁碰撞吸能示意图

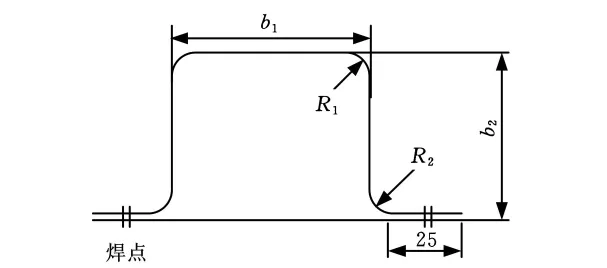
图3 薄壁梁的几何截面图

为了模拟整个碰撞过程并反求DP800的材料参数，笔者按照试验条件建立了其有限元模型，如图4所示，其碰撞仿真过程在非线性有限元软件LS－DYNA中进行。薄壁梁在高速碰撞过程中的快速塑性变形使得高强度钢DP800的温度迅速上升，导致材料产生温度软化效应，同时，高速碰撞过程中，高强度钢DP800的应变率变化范围也对仿真精度具有较大的影响。因此，本文采用综合考虑了温度软化效应、应变强化效应、应变率强化效应等影响的Johnson–Cook（J－C）本构材料模型，并以它作为碰撞仿真模型中高强度钢DP800的本构模型。

图4 薄壁梁的有限元仿真图

J－C模型是一种动态的本构模型，J—C模型的等效流动应力随温度、应变、应变率的变化而变化，其具体本构表达式为

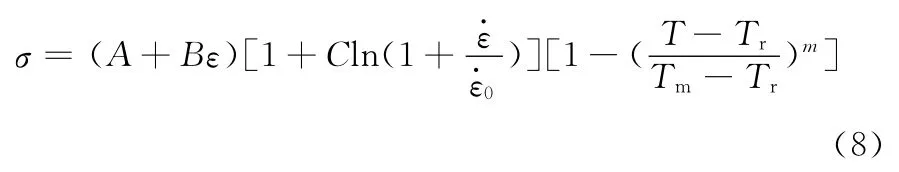
2.2 DP800材料参数的反求方法

本文采用小种群遗传算法对高强度DP800的材料参数进行反求，但是，如果遗传算法直接针对图4的有限元模型进行寻优，上千次的有限元模型的计算需要被执行，从而导致反求效率极其低下。因此，笔者采用序列响应面方法，在各次信赖域中构建设计目标的近似模型，而使得小种群遗传算法在近似模型上寻优，从而来提高整个参数反求过程的计算效率。反求过程即是使仿真曲线与该碰撞力曲线相逼近的过程，其逼近示意如图5所示。

图5 仿真与实验曲线逼近示意图

由图5可知，当实验曲线上的插值点较多时，要使得仿真曲线上的对应点与其逼近，将会调用大量的有限元计算，这就需要在仿真曲线与实验曲线的对应插值点之间都构建一个近似模型来解决该问题。由此可设立反求过程中的目标函数为

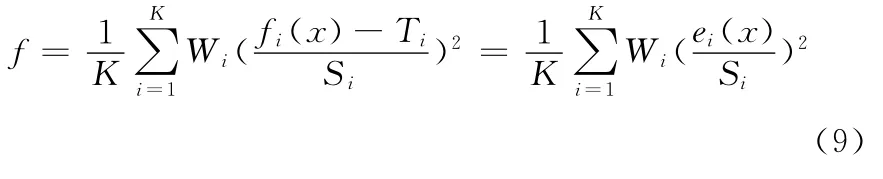
式中，K为插值曲线的点的个数；x为设计变量，x＝A，B，C，m，n；Wi为权重系数；fi（x）为响应面近似模型的计算值；Ti为实验测试点的值；Si为残差比例系数；ei（x）为残差值。

因此，DP800高强度钢板的材料参数反求问题即转化为以材料参数A、B、C、m、n为设计变量，以式（9）为设计目标的优化设计问题。其数学模型可以表示为

DP800薄壁梁材料参数反求过程可以表示为：首先对DP800梁进行碰撞试验，得到碰撞力与变形长度的试验曲线；然后，在整个设计空间中采用D最优试验设计采样样本点，从而构建DP800薄壁梁的各个试验曲线点的近似模型，并按式（9）形成目标函数；最终，通过在小种群遗传算法寻优及信赖域的移动和缩放来不断更新近似模型，直到优化收敛为止。DP800高强度钢材料参数反求的设计流程如图6所示。

图6 DP800材料参数反求流程图

2.3 DP800材料参数的反求结果及分析

基于序列响应面方法在信赖域内构建了如式（10）所示的目标函数，由于小种群遗传算法是通过交叉、变异等方式进行寻优的，不需要梯度信息，且在处理设计响应非线性程度高、不连续问题时，具有较好的全局最优搜寻能力，它也可以避免计算过早的收敛，并且在最优区域附近比普通遗传算法有更好的收敛性［13，15］，因此，本文采用小种群遗传算法迭代优化。经过8次设计空间的更新优化设计后，目标函数F收敛。DP800高强度钢板的材料参数A、B、C、m、n的初始值、8次优化迭代过程中的取值、设计目标F的初始值及最优值如表1所示。

由表1分析可知，优化设计过程经过8次响应面近似模型的更新与优化，设计目标F的收敛曲线如图7所示。材料参数A、B、C、m、n的信赖域的空间也逐渐缩小，材料参数反求过程共调用了81次DP800薄壁梁有限元计算模型，与直接采用传统优化算法的反求方法相比，序列响应面方法所需调用正问题的次数极大地减少，从而大大提高了DP800高强度钢板材料参数反求的效率。采用反求得到的材料参数A、B、C、m、n对薄壁梁进行有限元仿真计算，从而得到仿真运行的碰撞力与变形量曲线，它与试验曲线的对比如图8所示。

由图8的试验曲线与通过反求得到的材料参数A、B、C、m、n计算曲线的对比可以看出，两条曲线整体趋势上基本一致，各个峰值的位置也基本相同，从而验证了基于序列响应面的材料参数反求方法以及基于该方法得到的材料参数值的可行性与正确性。

表1 材料参数及设计目标的优化历程

3 结束语

本文提出了将序列响应面方法与小种群遗传算法相结合的材料参数反求方法，将材料参数反求问题转变为一优化问题，通过信赖域的缩放和更新来不断地提高近似模型的精度，使整个反求过程的效率得到大大提高，通过对比反求得到的材料参数的碰撞力与变形量仿真曲线与试验曲线可知，该方法反求的材料参数具有较高的精度，能够较好地达到工程应用的要求。同时，该方法能有效地减少材料参数获取过程中的试验次数，节约成本。

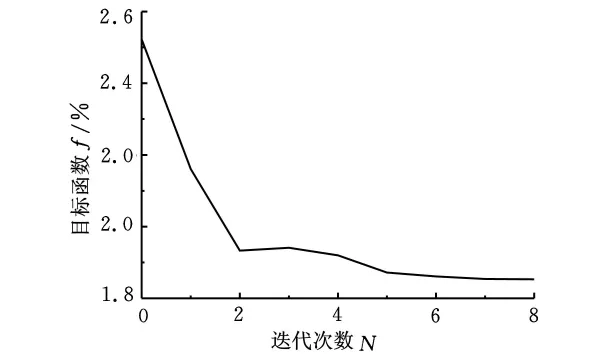
图7 目标函数收敛曲线

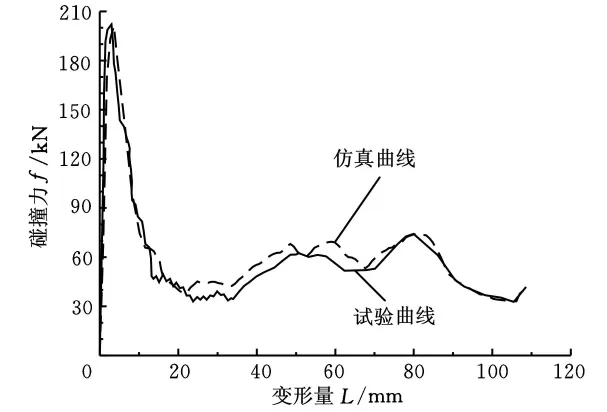
图8 试验与反求参数仿真曲线对比图

［1］ 钟志华，张维刚，曹立波，等.汽车碰撞安全技术［M］.北京：机械工业出版社，2003.

［2］ 曹银锋，李光耀，钟志华.金属成型材料参数的反求技术［J］.计算力学学报，2004，21（3）：292－296.

［3］ Kurtaran H，Eskandarian A，Marzouguiel D，et al.Crashworthiness Design Optimization Using Successive Response Surface Approximation［J］.Computational Mechanics，2002，29（4／5）：409－421.

［4］ Tarigopula V，Langseth M，Hopperstad O，et al.Axial Crushing of Thin－walled High－strength Steel Sections［J］.International Journal of Impact Engineering，2006，32（5）：847－882.

［5］ 郑刚，李光耀，孙光永.基于近似模型的拉延筋几何参数反求［J］.中国机械工程，2006，17（19）：1988－1992.

［6］ Nagel G M，Thambiratnam D P.A Numerical Study on the Impact Response and Energy Absorption of Tapered Thin－ walled Tubes［J］.International Journal of Mechanical Sciences，2004，46（2）：201－216.

［7］ Abedrabbo N，Mayer R，Thompson A，et al.Crash Response of Advanced High－strength Steel Tubes：Experiment and Model［J］.International Journal of Impact Engineering，2009，36（8）：1044－1057.

［8］ Han Haipeng，Taheri F，Pegg N.Quasi－static and Dynamic Crushing Behaviors of Aluminum and Steel Tubes with a Cutout［J］.Thin－walled Structures，2007，45（3）：283－300.

［9］ 谭飞，韩旭.基于代理模型的功能梯度梁的材料特性参数反求［J］.复合材料学报，2008，25（5）：176－180.

［10］ 刘迪辉，汪晨，李光耀.薄壁钢管材料参数反求［J］.中国机械工程，2008，19（6）：688－690.

［11］ Khalfallah H，Bel Hadj Salah H，Dogui A.Anisotropic Parameter Identification Using Inhomogeneous Tensile Test［J］.European Journal of Mechanics A／Solids，2002，21（6）：927－942.

［12］ Gelin J C，Ghouati O.An Inverse Method for Material Parameters Estimation in the Inelastic［J］.Computational Mechanics，1995，16（3）：143－150.

［13］ 韩利芬，高晖，李光耀，等.神经网络与遗传算法在拉延筋参数反求中的应用［J］.机械工程学报，2005，41（5）：172－176.

［14］ Redhe M，Forsberge J，Janssone T，et al.Using the Response Surface Methodology and the D－optimality Criterion in Crashworthiness Related Problems［J］.Structural and Multidisciplinary Optimization，2002，24（3）：185－194.

［15］ Liu G R，Han X.Computational Inverse Techniques in Nondestructive Evaluation［M］.Boca Raton：CRC Press，2003.