一种高精度在线测量大外径的方法和装置

赵前程 杨天龙 郭迎福

湖南科技大学机械设备健康维护省重点实验室，湘潭，411201

0 引言

对于大外径的测量，间接测量方法在测量范围、仪器的便携性、测量效率等方面具有明显的优势，其中具有代表性的测量方法包括滚轮法、三点法和圆周要素法等。目前天津大学和合肥工业大学［1－2］等机构都开展了滚轮法大直径测量的研究，但是为了减小误差影响和进行误差补偿，仪器结构和信号处理方法越来越复杂化；西南交通大学开展了三点法直径测量的研究，设计开发了一套用于火车车轮直径测量的检具［3］；杨宏宇等［4］基于标记法研制的智能大直径测量仪则采用圆周要素法中的角度弦长方法。

在根据圆周要素测量直径的仪器中，目前广泛使用的是弓高弦长类测量仪器。武汉理工大学、西南交通大学和湖南科技大学等研究机构积极开展了这方面的研究［5－7］，研究的关键问题在于如何提高弓高弦长法的直径测量精度。

针对弓高弦长法直径测量精度不高的问题，笔者设计开发了一套大外径高精度测量装置。该装置采用固定弦长、利用3个高精度激光位移传感器进行弓高的非接触相对测量等方法来保证弓高参数测量的高精度；通过2个不同尺寸的大圆盘对测量装置的初始弓高和弦长进行现场标定，以保证这2个参数标定的准确性；标定过程和测量过程采用在一个圆整周内多次采样求平均值的数据处理方法，可显著减小随机噪声等对直径测量结果的影响。采用以上技术措施显著降低了对装置本身的精度要求，测量系统结构简单、操作方便。该装置除了可以进行直径高精度测量外，基于3点误差分离技术同时可测量大轴的圆度误差［8］。

1 测量装置的结构设计

1.1 总体设计

测量装置由测试系统和标定系统两部分组成，其结构如图1所示。测试系统和标定系统放置在水平的大平板上，构成一个整体来进行测试系统初始弓高和弦长的标定。标定后的测试系统将单独使用，对待测大轴进行直径测量。

图1 测量装置结构示意图

测试系统的结构如图2所示，由3个高精度位移传感器、安装传感器的滑板、滑块、导轨、若干锁紧螺丝、底座、固定底座的云台、丝杠和螺母、3根圆导轨、三角架和计算机等组成。安装传感器的滑板用来调节传感器到被测大轴的距离；滑块沿导轨移动调节传感器的上下位置；云台上的丝杠和螺母保证测试系统整体位置沿3根圆导轨上下可微调；三脚架主要用来大范围地调整测试系统高度。

图2 测试系统结构示意图

标定系统的结构如图3所示，由一体化结构的直径分别为d1和d2的大圆盘、支撑旋转轴、轴承、测量转速的圆编码器、带动大圆盘旋转的调速电机、底座和支架等组成。测速编码器的作用是测量大轴转速，在标定时尽量使标定大轴的转速和加工设备上大轴的转速一致，以减小转速对测量精度的影响。

图3 标定系统结构示意图

1.2 主要几何参数的确定

首先根据被测大轴的直径，综合考虑测试系统的空间尺寸和弓高测量误差对直径测量结果的传递关系，合理选择弦长，一般说来，对于直径为d的大轴，弦长L＝2d／3左右比较合适。

根据被测大轴的直径d、弦长L和激光位移传感器的测量范围，确定标定大圆盘的大致尺寸d1＝d＋Δ和d2＝d－Δ，Δ为标定用的两个圆盘的直径相对待测大轴直径的上下偏移量。在传感器测量范围允许的前提下，Δ值应尽可能取大一些。由于大圆盘的直径将在三坐标测量机上进行测量标定，所以对其尺寸公差无需特别要求。用大圆盘对测量装置初始弓高和弦长进行标定时，大圆盘旋转，传感器在圆盘旋转一周期间高速采样，最后取采样结果的平均值，平均的过程将极大减小圆盘圆度误差对测试系统参数标定的影响，所以对圆盘的圆度误差也无需太严格的要求。

在三坐标测量机上分别对大圆盘的2个外圆一周进行密集均匀测量采样，得到圆周上N个点的坐标值，将采样得到的坐标值序列按照奇偶序号分成2个等长的序列，采用频域分析方法估计圆周的主要谐波分量和噪声强度σ，根据圆周轮廓的主要谐波分量重构轮廓，根据σ给出轮廓合理的公差范围，超差为异常数据予以剔除，最后采用最小二乘法计算圆盘直径

2 标定过程和方法

测量系统弦长和初始弓高的标定如图1所示。首先根据选择的弦长参数移动滑块12、13和14，使上传感器1和下传感器5射出光线之间的距离大致等于所选择的弦长，中间传感器3射出光线大致经过测量轴的轴心；然后将测量装置靠近标定圆盘，调节滑板2、4、6（即调节传感器到工件的距离），确保传感器到圆盘上测量点的距离在传感器的测量范围之内，锁紧滑板；最后开动电机，调节转速使标定圆盘的转速和待测大轴的转速基本一致后进行标定测量。

设圆盘轴线到上传感器1射出光线的距离为l1，到下传感器5射出光线的距离为l3，则定义上下传感器射出光线不对称误差为｜l1－l3｜。设测量圆盘D1时，上下传感器读数为S11和S13；测量圆盘D2时，上下传感器读数为S21和S23，传感器高度在测量两圆时变化微小，则当S11－S21＝S13－S23时表明上下传感器射出光线已对称，根据这一现象，调整其中的一个传感器高度，直到S11－S21＝S13－S23。然后上下调节滑块13，当传感器读数最小时，表明中间传感器射出光线已对中，锁紧各滑块。上述调节过程中传感器读数都是采用旋转一周多次采样取均值，以减小圆盘圆度误差和旋转误差等对对称调整和对中调整的影响。

当测试系统调节完毕后，即可实施对测试系统弦长和初始弓高的标定。设圆盘D1的弓高为初始弓高，记作H。将测试系统靠近圆盘D1，获得3个传感器一周的平均读数，分别为S11、S12和S13；同样地，将测试系统靠近D2，获得平均读数S21、S22和S23。3个传感器在一整周内采样N点，对于这N点数据采取与三坐标测量圆盘直径类似的方法进行数据处理，剔除异常值。记

则D1和D2的弓高差ΔH ＝S′2－S′1，且D2的弓高为H＋ΔH。

构造方程：

已知d1、d2和ΔH，解上面的方程即可求得L和 H，存储参数 H、L 和参数S11、S12、S13，完成测试装置的标定。

3 直径测量

测试装置一旦标定完毕，3个传感器的相对位置固定，不可再调节。在线测量加工过程中的大轴直径时，只需将测试系统安装在三脚架上，调节三脚架高度，并调节底座上的丝杠螺母，保证上下传感器对称要求，即保证S11－S31＝S13－S33即可。测量过程和测试系统的标定过程类似，数据处理方式相同。大轴旋转一周，传感器获得S31、S32和S33，则被测大轴的弓高为

被测大轴的直径为

4 仿真测量精度分析

文献［7］对中间传感器的对中精度、上下传感器的对称精度和传感器测量误差等因素对直径测量精度的影响作了仿真分析。在实际测量过程中，我们发现要满足对中要求还是非常困难的。进一步的研究发现，只需要在标定和测量时，传感器整体相对于工件轴线的上下位置偏移满足一定的要求即可，即在标定和测量时，需要对传感器上下整体偏移量进行一定的控制。下面仿真分析偏移量及圆盘标定误差对直径测量结果的影响，仿真参数如下：标定圆1直径d1取500mm，标定圆2直径d2取508mm，弦长L取400mm。

假设测量标定圆1时，上下传感器不对称误差服从3σ＝4mm的正态分布，中间传感器不对中误差服从3σ＝5mm的正态分布；测量标定圆2时，传感器整体位置存在相对测量圆1时3σ＝0.02mm的上下随机偏移；对待测大轴测量时，传感系统整体位置也存在3σ＝0.02mm的上下整体偏移。在上述条件下，对不同尺寸的大轴进行仿真测量，计算结果如表1所示。可以看出，待测大轴的直径测量误差小于1.5μm。所以标定和测量过程中对传感器的对称精度和对中精度要求不高，但是要控制测量时传感器系统整体位置的上下偏移量。

表1 直径仿真测量结果

两个标定圆D1和D2加工在一个圆盘上（图3），测试系统和标定系统放置于大平板之上（图1），所以在标定过程中测量标定圆1和标定圆2时，传感器的整体上下相对偏移很小，调整传感器位置保证S11－S21＝S13－S23的过程实际上是调整上下传感器的对称精度的过程。当圆盘直径约为500mm，弦长约为400mm，不对称度为10μm时，S11－S21和S13－S23相差约10μm。所以通过传感器的读数容易控制对称度不大于10μm。标定过程控制了上下传感器的对称精度，才能保证其后测量时传感器的整体上下偏移度要求。

标定完成后对待测大轴进行测量时，调整三脚架高度和丝杠螺母以满足S11－S21＝S13－S23的过程实际上是保证传感器整体上下偏移度的过程，传感器对20μm的偏移度反应灵敏，所以容易满足偏移度的要求。

另外一个影响测量精度的因素是标定大圆盘的直径标定误差。从标定方程和直径计算方程可以直接得到直径测量误差与待测大轴的直径呈线性关系。图4所示为标定圆1和标定圆2的直径标定误差分别为5μm和－5μm时，待测大轴的直径测量误差与待测大轴直径的关系曲线。

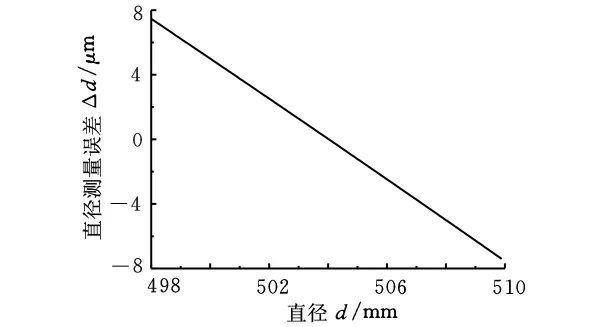
图4 直径测量误差与待测直径的关系

5 实际测量实验

首先我们选择LK－G30激光位移传感器进行弓高的相对测量，传感器的工作距离为30mm，测量范围为－5～5mm，将激光位移传感器与ML10激光干涉仪进行比对测量实验，发现其测量精度在1μm左右。

针对直径为505mm左右的大轴直径测量要求，考虑传感器测量范围，我们设计标定大圆盘的直径分别为508mm和500mm，测试系统的弦长设计为400mm。

在一个大圆盘上加工3个尺寸的外圆盘，在global三坐标测量机上进行标定，每个尺寸的圆盘上分别测量上中下3个截面，得到3个外圆的直径和圆度，如表2所示；按照图1的结构设计加工了如图5所示的测量装置。

表2 三个外圆直径坐标测量结果

图5 测量装置实物照片

将圆1和圆3作为标定圆对测试系统进行标定，然后对圆1、圆2和圆3分别在中间截面位置进行测量，按表2分别取直径为499.789mm、503.602mm和507.751mm。标定完成后，分别对3个直径进行20次测量。测量结果表明，对圆1和圆3的直径测量结果偏差小于±3μm；圆2的直径测量结果偏差大一些，在±4μm左右，可以看出测量系统可以达到±5μm的测量精度。

6 结束语

基于弓高弦长法直径测量原理，设计开发了大轴直径测量装置，分析了采用相对测量原理进行大轴直径测量的若干误差因素，提出了传感器安装的对中和对称精度不是影响直径精度的主要因素；标定圆盘的直径标定误差对测量精度有直接影响；测量时传感器相对待测大轴轴线的上下整体位置和标定时相对标定圆盘轴线的位置必须保持高度的一致性，并阐述了根据传感器读数控制传感器整体上下偏移量的方法。标定和测量过程采用多种数据处理方法提高了直径测量的精度。由于采用相对测量，当作为标定的圆盘尺寸标定精度足够时，直径测量精度容易得到满足。下一步将在系统中增加三点误差分离算法程序，以实现系统对大轴圆度误差的测量。

［1］ 史庆伟，张国雄，李真.滚轮法大直径测量精度研究［J］.天津大学学报，2005，38（12）：1083－1087.

［2］ 金施群，丁晓牧，费业泰，等.大轴直径的高精度多滚轮法测量［J］.应用科学学报，2005，23（2）：200－203.

［3］ 孙效杰，周文祥，邹晓霞.大直径间接测量方法的比较［J］.工具技术，2009，43（3）：95－98.

［4］ 杨宏宇，谢丽霞，殷镇良.高精度大直径测量的新方法研究与实现［J］.仪器仪表学报，2000，21（6）：597－600.

［5］ 张英春，周文祥.WP－C型铁路车轮外形测量仪直径标定方法的不确定度分析［J］.铁道车辆，2008，46（12）：3－5.

［6］ 陈满意，卢振伟.基于弓高弦长的大型圆柱体直径测量的不确定度研究［J］.机械制造，2009，47（541）：80－82.

［7］ 赵前程，陆长友，罗晓莉.大直径在线高精度测量不确定度研究［J］.机械科学与技术，2009，27（9）：1247－1251.

［8］ 魏元雷，洪迈生，苏恒，等.平行三点法圆度误差分离技术的精度分析［J］.机械科学与技术，2003，22（1）：51－54.

［9］ 赵前程，罗晓莉，邓善熙.基于特征模型的形状误差估计新方法［J］.仪器仪表学报，2007，28（9）：1629－1633.