金属带式无级变速器带轮变形研究

张 武 周春国 刘 凯

西安理工大学,西安,710048

0 引言

金属带式无级变速器(continuously variable transmission,CVT)是迄今为止应用最成功的车辆无级变速器之一。大量实践表明,装有金属带式无级变速器汽车的动力性、舒适性及排放比装液力自动变速器和手动机械变速器的汽车更佳。金属带不同于橡胶带,它是组合带,其弹性变形小,一般与带轮弹性变形相比较可以忽略不计。本文分析了带轮弯曲变形并假定其纵向和横向为无限刚性。Gerbert[1]认为带轮变形有三种型式,即局部变形、平面变形和挠曲变形。局部变形是带轮曲面和带侧面之间的局部弹性变形;平面变形与带轮特性有关,它产生的面变形与局部作用力无关;带轮挠曲变形是由于两个半片带轮的制造公差以及它们相互间移动所造成的。由于在变速箱寿命内公差可能是变化的,并且带轮开始安装时仅存在较小挠曲,到寿命的后期则存在较大挠曲,所以模拟带轮挠曲变形是比较困难的。Satter[2]考虑了带轮的轴向变形和挠曲变形及纵向和横向刚度、金属带的偏斜等因素对带轮变形的影响,采用有限元分析方法对带轮变形进行了类似的研究。Akehurst等[3]采用金属带变速器试验台[4]测量带轮变形,试验结果包含金属带弹性变形和安装造成的挠曲变形两部分。Akehurst等[3]用一个度盘测量仪来测量最大半径时带轮的轴向变形,其试验结果表明：带轮变形和轴向推力有一定的关系,且带轮外侧的变形较明显。由于试验条件有限,本文借助ANSYS软件对带轮变形进行分析,结果表明,带轮变形具有一定的规律性。该结论为带轮的结构优化设计等提供了理论依据。

1 带轮模型

金属带式无级变速器的主从动轮在形状和尺寸上一致,由于变速器在工作过程中力矩有损失,故主动轮轴向推力较从动轮轴向推力大[5]。对于本文中所研究的CVT模型,主动轮上作用有恒定的角速度和驱动力矩,从动轮上作用有恒定的负载。此模型可以很好地研究金属带组件从进入带轮到离开带轮过程中带与带轮间的相互作用关系。基于以下假设建立模型并对其进行分析：①金属带组件是连续的;②金属带长度恒定不变;③忽略带的抗弯刚度和抗扭刚度;④带与带轮间的线接触与带轮轴线平行。

文献[6]认为带轮弹性变形严重影响了金属带CVT传动比的改变和组件间的滑动问题,进而影响到效率。图1所示为带轮变形模型,用三角函数描述的带轮槽角度和带轮轴向宽度的变化如下：

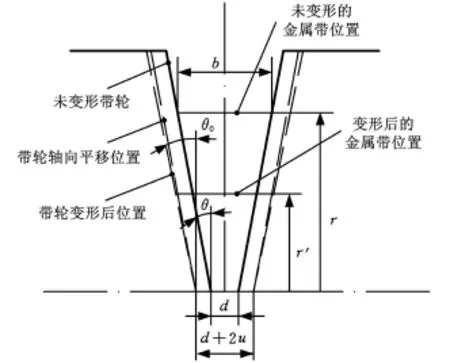
图1 带轮变形模型

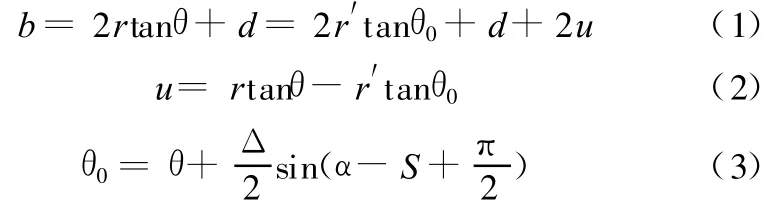
式中,θ为未变形的带轮槽角度;θ0为变形后的带轮槽角度;Δ为带轮槽角度变化幅度;α为角坐标;S为带轮楔热膨胀角;u为带轮轴向宽度变化量;r为未变形时主动轮上带的工作半径;r′为未变形时从动轮上带的工作半径。

Δ是一个微小的量,但是它却影响了变速过程中带轮轴向推力的大小,在传动比变化过程中它不能被认为是恒定不变的[2,7]。参考文献[6,8]建议采用如下公式对其进行确定：

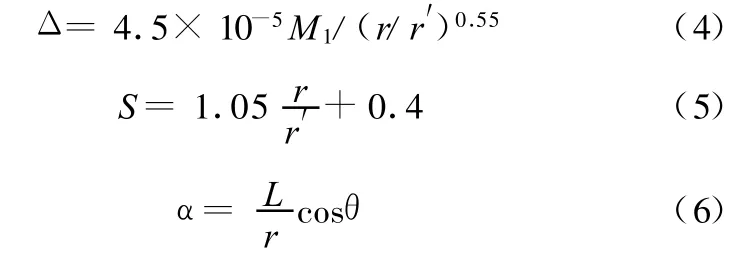
式中,M1为主动轮输入力矩;L为金属带长度。

2 算例分析及讨论

图2是VDT公司生产的P811型CVT的基本结构[9],主从动轮各包括一个固定半片带轮和一个移动半片带轮,由于移动半片带轮受到均布的液压力及较好的约束条件,其受力工况较固定半片带轮要好。本文对固定半片带轮进行研究,即以下提到的主从动轮均指主从动轮固定轮部分。确定整个CVT的结构尺寸如下：主从动轮工作半径r=31.5～74mm,传动比i=0.42～2.35,最大输入扭矩M 1=160N◦m,最大输入转速n=6000r/min,额定功率P=70k W。

用Solidworks软件建立带轮三维模型并进行相应简化,将其导入ANSYS软件进行有限元分析。为了提高计算精度,减小计算规模,本文采用映射网格方式对模型进行划分。图3是单元类型为六面体的带轮模型。对带轮内圆柱面实施全约束,内侧受力面上作用力F=24.93k N,外侧受力面上作用力 F=27.56kN[9],图4、图 5分别表示NDIV No.of element division等于10、20和30时,带轮内外侧变形和应力的计算结果。

图2 带轮基本结构

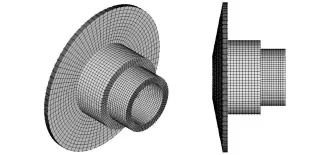
图3 带轮有限元网格模型

由图4所示可以看出：带轮在工作区域发生了变形,由于工作半径较小,所以工作区域在整个圆周方向上占2.86rad;在带轮内侧,变形量h始终保持在 3 ～ 4μm(3.3μm,4.04μm,3.86μm)之间,因为整个模型的约束在带轮内圆柱面上,带轮内侧距此约束面较近,又因为带轮内侧的实体较外侧大得多,所以导致带轮内侧的变形较小;而应力σ却是不断增大的(81.9MPa,131MPa,218MPa),造成此结果的主要原因是当网格不断细化时,每个网格所从属的受力面积不断减小,因此导致应力的不断增大。由图5所示可以看出：带轮工作半径较大,所以工作区域在整个圆周方向上占3.42rad;在带轮外侧,变形量则始终保持在一个较大的数值上(136μm,140μm,136μm),即140μm左右,与内侧带轮变形相反,由于距离约束面较远,可以将其近似理解为变截面悬臂梁的受力状态,所以外侧变形较大;其应力的变化和带轮内侧应力变化趋势是一致的,只是应力增长的速度较内侧缓慢(155MPa,214MPa,228MPa),其主要原因是内侧作用面积较外侧小,当网格不断细化时,内侧网格从属的受力面积较外侧减小的更剧烈,造成了此种现象。由以上分析可以得出：对于本文用规则六面体划分的网格模型,当受力面上的作用力和模型约束不变时,网格细化对变形的结果没有影响。

参照以上结论,以下对带轮在各个工作半径时的变形和应力进行分析,其仍采用规则六面体划分的网格模型,NDIV No.of element division选择20。图6和图7所示分别为在传动比由小到大的变化过程中,主从动轮在相应传动比时,其各自所受的轴向推力及工作半径的变化规律[9]。由于带轮在各个工作半径时的变形和应力云图与图4、图5类似,因此不再展示云图,只将计算结果提取出来,根据其与传动比的关系绘出图8和图9。

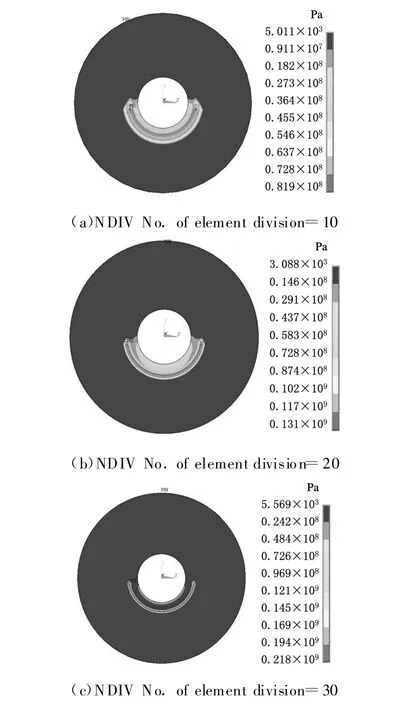
图4 带轮内侧应力云图

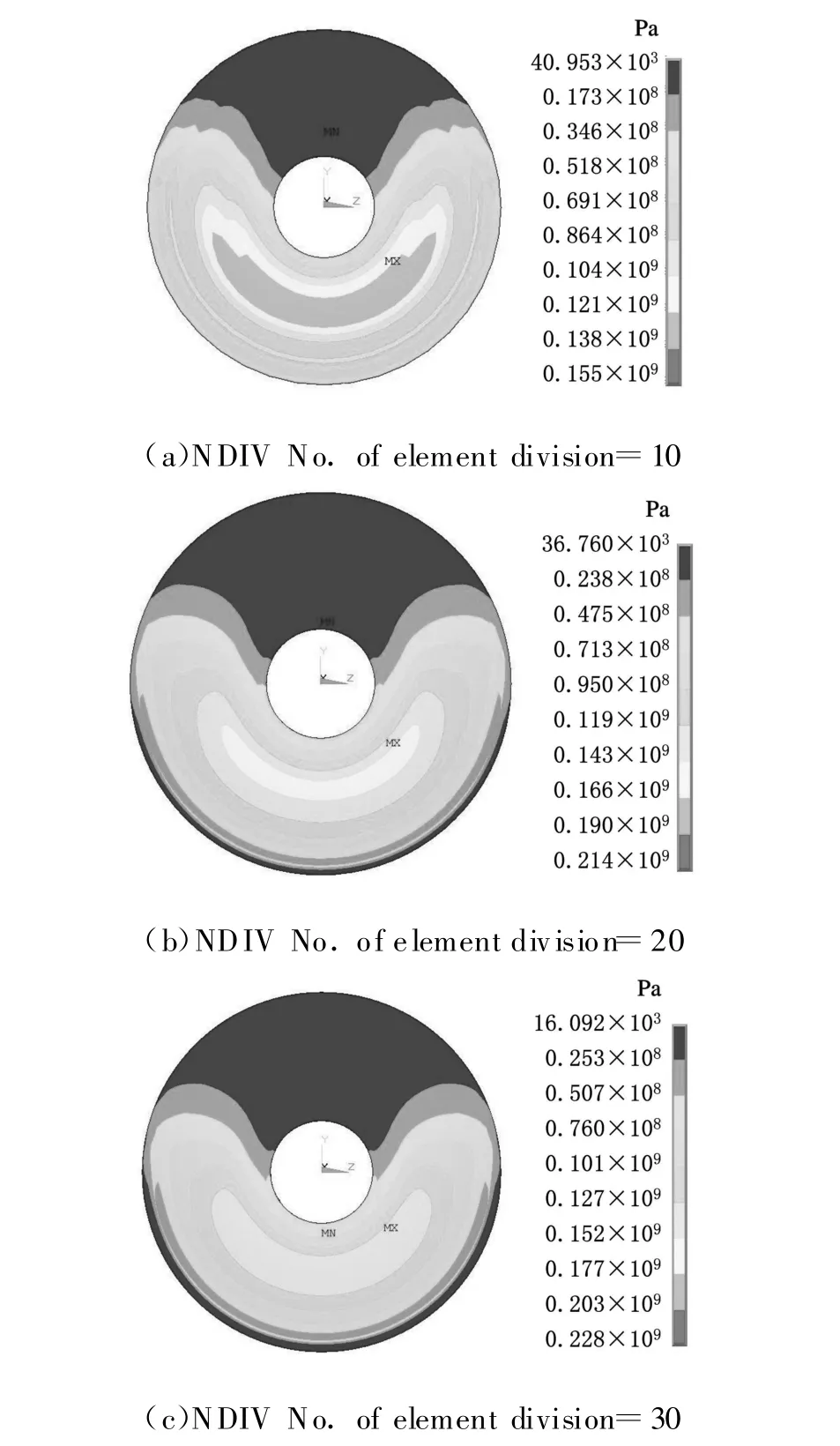
图5 带轮外侧应力云图

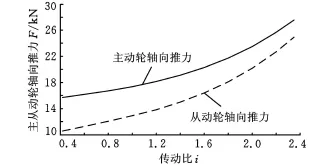
图6 主从动轮轴向推力与传动比的关系

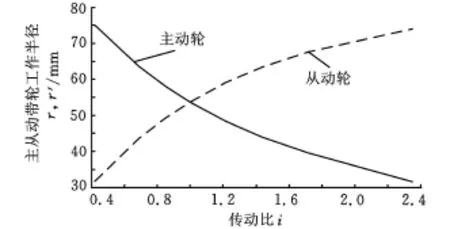
图7 主从动轮工作半径与传动比的关系

由图8所示可以得出：由于主动轮工作半径随着传动比的增大而减小,致使实体增多和约束效应增强,所以主动轮变形量随之减小。尽管最小半径处主动轮轴向推力27.56kN比从动轮轴向推力10.5kN大一倍多,但其4μm的变形量比从动轮的1.54μm相差无几,两者都可以忽略。由此足以说明约束对变形的影响很大,尤其在带轮工作半径较小时起决定性作用。而从动轮变形则是随着传动比的增大而增大的。主从动轮最大工作半径为74mm时,主动轮轴向推力为15.5kN,变形量为87.2μm;从动轮轴向推力为24.93kN,变形量为140μm。主动轮变形量小于从动轮的变形量,所以当作用力远离约束面时,变形量的大小很大程度上取决于作用力的大小。由图9所示可以看出：从动轮应力随着作用力的增大而增大;主动轮前半部分应力的递减则是主要由悬臂梁效应造成的,后半部分则是由作用力的急剧增加和受力面的快速减小造成的,在此过程中,主动轮工作半径44.3mm处为转折点。

Akehurst等[3]采用金属带变速器试验台[4]测量带轮变形,由于考虑了金属带弹性变形和安装造成的挠曲变形两部分,其试验数值较本文的计算数值大一些,但在趋势上是一致的,本文得出的带轮外侧变形较大的结论与其试验结论相一致。

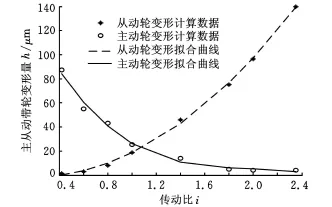
图8 主从动轮变形量与传动比的关系

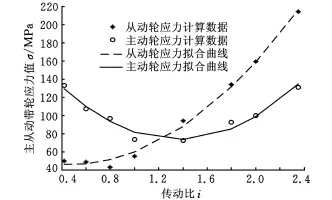
图9 主从动轮应力与传动比的关系

3 结论

(1)当受力面上的作用力和模型约束不变时,网格细化对变形的结果没有影响。

(2)主动轮变形量随着工作半径的减小而减小,应力则是先减小后增加;从动轮变形量和应力都随着工作半径的增大而增大。

(3)当传动比i=1.46,即主动轮工作半径为44.3mm时,主动轮上产生最小应力71.8MPa。

[1] Gerbert G.Skew V-belt pulleys[C]//International Conference on Continuously Variable Transmissions,CVT'96.Yokohama,1996：11212.

[2] Sattler H.Efficiency of Metal Chain and V-belt CVT[C]//Proceeding of CVT'99.Congress.Eindhoven,1999：99-104.

[3] Akehurst S,Vaughan N D,Parker D A,et al.Modeling of Loss Mechanisms in a Pushing M etal V-belt Continuously Variable Transmission.Part 1：Torque Losses due to Band Friction[J].Part D：Journal of Automobile Engineering,2004,218(11)：1269-1281.

[4] Akehurst S,Vaughan N D,Parker D A.The Effect of Lubricant Temperature on the Loss Mechanisms Associated with an Automotive Metal V-belt CVT[C]//2000 CEC/SAE International Spring Fuels and Lubricants Meeting and Exposition.Paris,2000：20121872.

[5] 阮忠唐.机械无级变速器设计与选用指南[M].北京：化学工业出版社,1999.

[6] Sferra D,Pennestri E,Valentini P,et al.Dynamic Simulation of a Metal-Belt CV T Under Transient Conditions[C]//Proceedings of the ASME Design Engineering Technical Conference.Montreal,2002：261-268.

[7] Carbone G,Mangialardi L,Mantriota G.The Influence of Pulley Deformations on the Shifting Mechanism of Metal Belt CVT[J].Journal of Mechanical Design,2005,127(1)：103-113.

[8] Srivastava N,Haque I.Transient Dynamics of the Metal V-belt CVT：Effects of Pulley Flexibility and Friction Characteristics[J].Journal of Computational and Nonlinear Dynamics,2007,2(1)：86-97.

[9] 张武.车用金属带式无级变速器传动性能分析与形线研究[D].西安：西安理工大学,2009.