分形理论在齿轮接触应力分析中的应用研究
2010-05-30陈奇赵韩黄康徐顺
陈 奇 赵 韩 黄 康 徐 顺
合肥工业大学,合肥,230009
0 引言
齿轮齿面间的接触状况和应力大小将直接影响到两接触轮齿的寿命和运行状态。目前,关于齿轮的承载能力分析的理论很多,比如Hertz理论和有限元理论。通过Hertz模型可计算出齿轮接触面的接触应力,由此可判断出接触体能否满足接触强度条件,并能对其承载能力进行一定的参数选择和优化分析。Hertz模型较正确地反映两接触体间的应力状态,仍应用于现代产品设计中。
然而,Hertz方法存在如下两个问题:①不能正确计算内啮合的两齿轮在其接触处的曲率半径相等时的应力,如微线段齿轮[1-3]在以凸凹啮合齿轮啮合时,其两齿轮接触处的曲率半径几乎相等,用Hertz理论或有限元理论计算时所得到的应力值几乎为零,这显然与实际情况不符。②仅考虑两齿轮的宏观因素(如表面的形状、物体的材料特性),而没有考虑两齿轮的微观特性因素,如接触表面的形貌特征及其表面粗糙度等对接触能力的影响。若取两个加工方法、材料特性和受载都一样的齿轮进行接触啮合,若其表面粗糙度和表面纹理形状不一样时,其运行状态和质量显然是不一样的。
有限元理论属于近现代理论,通过把齿轮齿面进行网格划分,并设定一定的边界条件和载荷,然后通过求解刚度矩阵方程等步骤,分析出齿轮接触的情况[4-7](如应力大小和变形情况)。目前流行的有限元理论的软件有ANSYS软件、Nastran软件等。有限元理论能够反映出齿轮的承载的状况,但亦存在以下不足:①同样主要考虑接触体的宏观因素,未考虑接触体的微观因素。②计算结果受影响因素多,计算结果不够准确,大多只能反映一定的应力和形变的趋势。当选择的单元类型、划分网格的大小、边界条件、加载方法、计算方法等其中的一个因素发生改变时,得到的计算结果便不同。③计算过程繁琐,不具通用性。有限元计算需要建模、划分网格、设置边界和载荷等步骤,整个分析过程复杂,不易掌握。
为了解决上述问题,本文在前期研究成果的基础上[8],进一步研究分形理论在齿轮接触强度中的应用,从而验证理论的正确性和实用性。
1 齿轮分形接触强度模型的建立
1.1 齿轮表面接触系数
由文献[9-10]知,渐开线轮廓上各点的曲率并不相同,沿工作齿廓各点所受的载荷也不同。对于端面重合度εa≤2的直齿轮传动,以小齿轮单齿啮合区的外界点产生的接触应力最大,而两啮合齿轮节点处的计算接触应力与单齿啮合区的外界点的计算接触应力极为相近。因此为计算方便,通常以节点啮合为代表进行齿面的接触强度计算。
设齿轮的基本参数如下(图1):齿数z,法向模数m n(端面模数 m t),法向压力角αn(端面压力角αt),螺旋角β,变位系数 x n(端面变位系数 x t),齿顶高系数h*a(n)(端面齿顶高系数h*a(t)),顶隙系数c*n(端面顶隙系数c*t),齿宽b,则
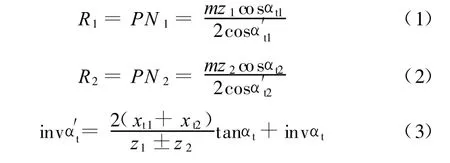
式中,R1为齿轮1、齿轮2齿面在M点接触时,齿轮1接触齿廓处的曲率半径;R2为齿轮1、齿轮2齿面在 M点接触时,齿轮2接触齿廓处的曲率半径;z1、z2为两齿轮齿数;αt1 、αt2 为两齿轮的端面压力角;α′t1、α′t2为两齿轮无侧隙 啮合的端面啮合角;xt1、xt2为两齿轮的端面变位系数;“+”为外啮合,“-”为内啮合。
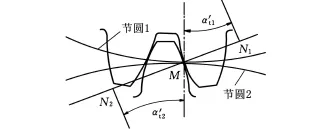
图1 两齿轮接触模型
由文献[8]有
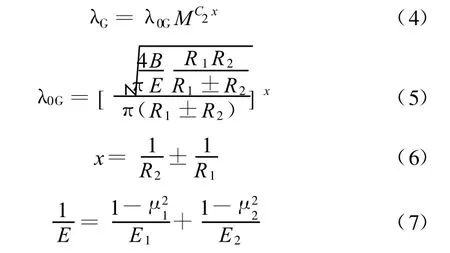
式中,λG为齿轮表面接触系数;λ0G为初始齿轮表面接触系数;P为单位线长度载荷;B为两圆柱体有效接触长度;E为综合弹性模量;μ1、μ2为齿轮1、齿轮2的泊松比系数;E1、E2为齿轮1、齿轮2的弹性模量;C2为常数,C2=0.5;x为综合曲率系数。
1.2 齿轮分形接触模型公式的建立
设a c[11-12]为单个微突体由弹性变形变化到塑性变形的临界面积,a l为最大接触点的面积。将式(5)代入相关公式[10]可得齿轮的分形接触模型,即求得齿轮接触面的接触力与接触面积的关系。
(1)若a l>a c,两球体发生弹塑性变形,此时的载荷又可分下列两种情况:
当D≠1.5时

式中,D为接触齿面轮廓的分形维数;P′*为量纲一载荷,P′*=P/(AaE),这里Aa为名义接触面积,可由谱特性参数 ωl确定为当两平面轮廓接触且D≠1.5时的名义载荷;A′r*为量纲一真实接触面积,A′*r=Ar/Aa,这里 Ar为两齿面间总的真实接触面积和[11],为粗糙度幅值参数;φ为齿轮材料的特性参数,φ=σy/E,σy为较软齿轮材料的屈服强度;K为齿轮硬度 H与屈服强度σy的相关系数,K=H/σy;a*c为量纲一结合面间的临界接触面积;g1(D)、g2(D)均为与分形维数有关的常数;G为反映z(x′)大小的特征尺度系数;z(x′)为随机轮廓高度;x′为轮廓位移坐标。

式中,P2*(A*r)为当两平面轮廓接触且D=1.5时的名义载荷。
(2)若a l<a c,仅发生塑性变形,此时
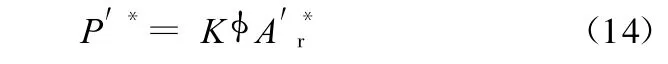
式(8)~式(14)即是两齿轮表面接触的分形模型。
1.3 微线段齿轮的分形接触公式
因微线段齿轮啮合对的接触处的曲率半径相等[3],即R1=R2时,由数学推导可得λ0G=1,将λ0G=1代入式(8)~式(14)即可得到微线段齿轮的分形接触公式。
(1)若al>ac,两球体发生弹塑性变形,此时的载荷又可分下列两种情况:
当D≠1.5时
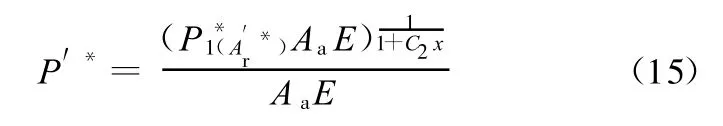
当D=1.5时

式(15)~式(17)即是微线段齿轮轮齿表面接触时的分形模型。
2 分形模型结果预测
2.1 齿数对模型预测结果的影响
取三对渐开线齿轮啮合对,齿数分别为25和83、40和 83、83和83。各啮合对齿轮其余参数均相同。利用上述公式可得到不同齿数时的载荷与真实接触面积的关系如图2所示。由图2可知:①在其余变量和z1不变时,不论是内接触或外接触,随着z2增加,相同载荷下将得到更大的真实接触面积,接触应力下降。因此,适当的增加齿数是有利的,即适当增加齿轮的尺寸对降低接触强度有利,这与传统的Hertz理论一致,因此分形分析结果是正确的。②内接触比外接触要好。③当z2与z1相等时,P*并不为零,从而证明了该模型可用于解决内接触曲率半径相等时的接触强度计算问题。
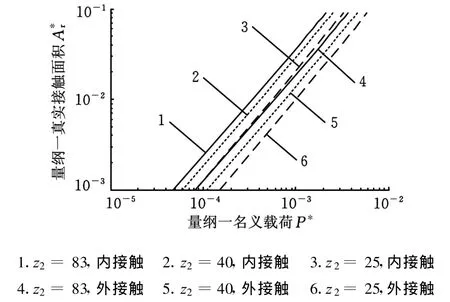
图2 齿数对模型预测结果的影响
2.2 粗糙度幅值参数对模型预测结果的影响
由文献[12]知,G*主要反映材料的表面性质。由图3可知,降低G*使曲线往上运动,因此降低G*能有效降低接触强度,从而改善表面接触性质。这一结论与实际情况相吻合。另外,相同接触条件,内接触的接触应力要低些。
3 齿轮接触强度实例计算
取一对标准渐开线直齿轮啮合,参数如下:小齿轮齿数z1=25,大齿轮齿数z2=83,驱动力矩为9.5×104N◦mm,模数m=2mm,压力角α=20°,齿宽b=17mm,弹性模量E=206GPa,泊松比μ=0.3,变位系数为0,设齿轮为6级精度。

图3 参数G*对模型预测结果的影响
3.1 Hertz方法计算
齿轮的接触应力计算公式为[10]

式中,α为标准渐开线齿轮的分度圆压力角;u为传动比,u=z2/z1;KH为载荷系数;T为小齿轮受到的扭矩;b为小齿轮的齿宽;d1为小齿轮的分度圆半径。
选取K=1.2,并将齿轮其他参数代入式(18)可得齿轮接触的最大应力为 σH=1025.8MPa。
3.2 有限元法计算
(1)建立齿轮接触几何模型。参照文献[13]方法,可在Pro/E中精确建立两齿轮几何模型,为提高有限元计算效率,模型各取齿轮的3个齿。通过中心距和分度圆上的啮合点约束,使两齿轮装配。通过Pro/E与ANSYS的数据接口,或将模型保存为igs格式导入到ANSYS中。模型如图4所示。
(2)设置单元类型。由于为平面问题,在ANSYS中选择四节点四边形板单元PLANE182。
(3)网格划分。设置网格精度为4级,划分网格图形见图4。
(4)定义接触对。选择小齿轮和大齿轮相应接触齿廓上的所有节点,创建节点集Nodes1和Nodes2。根据接触定义向导按钮,选择小齿轮为目标面,大齿轮为接触面,并选择面-面接触方式,完成接触对定义。
(5)设置边界及载荷。将坐标系转成柱面坐标后,将小齿轮内边缘节点的径向位移固定,大齿轮内边缘节点的各个方向位移固定。载荷为加在小齿轮上的转矩,具体方法是把载荷分别加载到小齿轮内径方向上各节点。载荷F r=-792N。加载结果如图5所示。
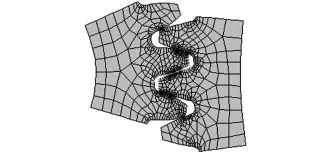
图4 ANSYS模型及网格划分

图5 ANSYS模型加载图
(6)求解。在Analysis Options(求解类型)下拉列表中选择Large Displacement Static,并设置计算时间为1,载荷步为20,即可求解。
(7)结果显示及分析。由图6可见,齿轮间最大的应力位于接触处,其值为983MPa。
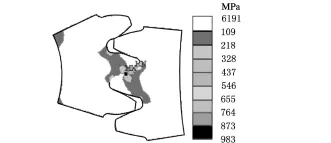
图6 ANSYS求解结果应力云图(啮合对局部放大图)
3.3 分形模型方法计算
在应用分形模型前,需要先确定其中的3个主要参数:分形维数D、粗糙度幅值参数G*、齿轮材料特性参数φ。
(1)分形维数D。根据葛世荣等[12]的研究:磨削表面分形维数与粗糙度Ra的关系及它们之间的近似换算式为

Ra值对应为微米级数值大小。取Ra=0.8,计算得D=1.54。
(2)粗糙度幅值参数G*。粗糙度幅值参数G*用来控制微观数量级大小的参数。根据参考文献[12-14],在本例中取G*=10-6。
(3)材料性质参数[15]为

将 σy=550MPa、E=206GPa代入式(20)得φ=2.67×10-3。
将上述三参数代入式(8)~式(14),并通过MATLAB编程可求得两齿轮间的接触应力:σH=1017.5MPa。
3.4 算例对比分析
表1给出了前面3种计算结果方法的对比数据。
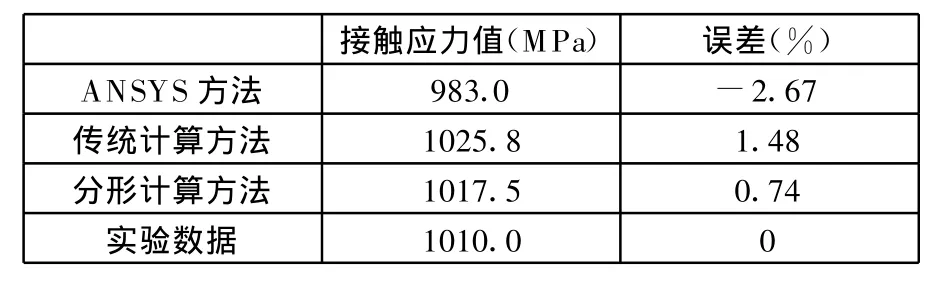
表1 各种方法计算接触应力数据的对比
由表1可见,3种方法所得结果基本上一致,其中ANSYS方法的误差稍大一些,分形计算方法与传统计算结果最接近。因此,证明了文中所述方法是可行的。
4 结论
(1)本文在分形接触理论和前期研究成果的基础上,建立了齿轮接触强度计算的分形模型。该模型不仅能解决Hertz理论不能解决的内接触曲率半径相等时的齿轮啮合问题,而且计算公式具有通用性,计算结果更为精确。
(2)本文分别运用传统Hertz理论、有限元理论和分形理论对实例进行对比计算,证明了分形理论应用于齿轮接触强度计算的可行性。
(3)在利用分形理论模型进行计算时,其中的参数如分形维数D、粗糙度幅值参数G*为近似取值,而没有真实的试验测量数据,随着接触对齿轮材料等特性的不同,其值存在差异。因此在下面的工作中主要关注齿轮分形接触模型的试验研究。
[1] Komori T,Ariga R,Nagata S.A New Gear Profile Having Zero Relative Curvature at Many Contact Points Logix Tooth Profile[C]//Proc.of International Power Transmission and Gearing Conference.Chicago :ASME,1989 :599-606.
[2] 赵韩,梁锦华,刘红雨,等.微线段齿廓的形成原理及特性[J],机械工程学报,1997,33(5):7-11.
[3] 刘红雨,赵韩,梁锦华.微段渐开线齿轮接触强度与弯曲强度的分析[J].上海理工大学学报,2003,25(3):77-80.
[4] 杨汾爱,张志强,龙小乐,等.基于精确模型的斜齿轮接触应力有限元分析[J].机械科学与技术,2003,3(2):206-208.
[5] 叶友东.基于ANSYS的渐开线直齿圆柱齿轮有限元分析[J].煤矿机械,2004(6):43-45.
[6] 周秦源,孔远翔,米建龙,等.基于Pro/E和ANSYS的齿轮接触应力的有限元分析[J].沈阳航空工业学院学报,2007,24(4):34-37.
[7] 胡建生.利用CAXA与ANSYS实现圆柱齿轮强度校核[J].辽宁工学院学报,2007,27(3):192-194.
[8] 黄康,赵韩,陈奇.两圆柱体表面接触承载能力的分形模型研究[J].摩擦学学报,2008,11(6):529-533.[9] 郑文纬,吴克坚.机械原理[M].北京:高等教育出版社,1997.
[10] 濮良贵,纪名刚.机械设计[M].7版.北京:高等教育出版社,2001.
[11] Bhushan B.Introduction to Tribology[M].New York:John Wiley&Sons,2002.
[12] 葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005.
[13] 张训福,黄康,陈奇.渐开线齿轮齿根过渡曲线方程的建立及三维精确建模[J].组合机床与自动化加工技术,2008(2):1-5.
[14] 葛世荣.粗糙表面的分形特征与分形表达研究[J].摩擦学学报,1997,17(1):73-80.
[15] 徐顺.基于分形理论的齿轮接触模型的研究[D].合肥:合肥工业大学,2008.
