广东省结核病发病趋势的时间序列分析

钟球 蒋莉 周琳 李建伟 陈瑜晖 连永娥

(广东省结核病防治研究所 广州 510630)

广东省结核病发病趋势的时间序列分析

钟球 蒋莉 周琳 李建伟 陈瑜晖 连永娥

(广东省结核病防治研究所 广州 510630)

目的利用乘积季节模型预测广东省结核病的发病趋势,为制订结核病的防控措施提供科学的依据>。方法利用最小二乘法原理,应用自回归求和移动平均模型与随机季节模型相结合的乘积季节模型,对广东省结核病发病趋势进行预测>。结果利用1996年至2008年资料构建ARIMA(0,1,1)(0,1,1)4模型,所建立的模型的预测效果良好,实际值均在预测值的95%可信区间内>。结论采用ARIMA乘积季节模型预测广东省结核病发病情况,拟合及预测效果较好,预测结果符合全省发病现状及当前采取的防控措施。

结核,肺/预防和控制;结核,肺/流行病学;发病率;时间;广东省

我国是全球22个结核病高负担国家之一,每年新发结核病人估算数居第2位。由于我国结核病疫情严重、流行广泛,使得国内疫情下降速度缓慢。特别是近年来,由于城市和农村的环境发生了巨大的变化,流动人口的增加、TB/HIV双重感染和耐药病人的出现,使结核病发病和流行模式变得十分复杂,如果能对结核病的发病进行准确的预测,将对结核病防治工作起到极大的推动作用[1]。因此,本文尝试利用美国学者Box和英国Jenkins提出的自回归求和移动平均模型(autoregressive integrated moving average,ARIMA)与随机季节模型(stochastic seasonal model)相结合的乘积季节模型(product seasonal model)建立结核病发病预测模型,对结核病报告发病率进行分析、预测,为结核病控制提供科学依据。本研究利用拟合的数学预测模型,对2010年及2011年的结核病报告发病率进行外部预测,以探讨该模型在该领域应用的价值。

1 资料与方法

1.1 资料来源 用于预测的结核病登记发病率资料,来源于广东省1996年至2009年每季度登记的新涂阳肺结核患者人数及广东省统计年鉴1996年至2009年全省人口数。

1.2 研究方法 采用SPSS13.0录入人口及每季度新涂阳肺结核患者登记情况资料,根据1996年至2008年每季度的报告报告发病率建立ARIMA乘积季节模型,用2009年的数据评价模型的预测效果,对2010—2011年的疫情进行外部预测和分析。

1.3 时间序列模型的建立 为选择1个最优的预测模型,完整的ARIMA过程包括[2]：①序列平稳化：ARIMA的应用需要时间序列符合平稳性的要求;②模型的识别：主要是根据ACF图和PACF图的特征,提出几种可能的模型作进一步分析;③模型参数估计和模型诊断：对提出的模型进行参数估计和诊断,如模型不恰当,则回到第二阶段,重新选定模型;④预测应用：1996年～2008年的数据用于建立模型,2009年的数据用于验证模型的预测效果。

2 结果

2.1 结核病发病的趋势分析 对1996年至2009年各季度的新涂阳肺结核登记发病率绘制时间序列分布图(图1)。由图1可以看出,新涂阳肺结核登记发病率呈现明显的季节变动规律,且年内呈现波动现象,基本规律为每年1、4季度登记发病率较低,

2、3季度登记发病率高。

2.2 模型的建立

2.2.1 序列的平稳化 在对原始数据进行取自然对数和 1阶差分转换后,做序列自相关图,发现ACF序列在4、8、12、16处都有一个局部极大值,说明存在周期为4的季节性周期,再进行一次季节性差分消除季节因素的影响后,原始资料由明显震荡特征的非平稳序列,转化为近似平稳的时间序列,符合ARIMA模型的平稳性要求。

2.2.2 模型的识别 根据差分变换的次数,可以确定模型形式为：ARIMA(p,1,q)(P,1,Q)4,其中p,q和P,Q是待定的参数,分别表示连续模型和季节模型中的自回归阶数和移动平均阶数。4表示季节模型以4个季度为周期。由于差分后自相关系数在P＞1后骤减,偏自相关系数递减但拖尾,根据以上特征初步判断连续模型为ARIMA(0,1,1)或ARIMA(0,1,2)[3]。季节模型的参数P、Q判断较为困难,但根据文献,参数超过 2阶的情况很少见[4-5],可以分别取0、1、2由低阶到高阶逐个试验,根据模型的拟合优度、残差情况以及系数间的相关性进行综合判断,直至得到最佳模型。

图1 1996—2009年新涂阳肺结核季度报告发病率时间序列分布情况

表1 备选模型的参数估计

表2 2009年各季度新涂阳肺结核报告发病率实际值与预测值比较

2.2.3 参数估计与模型检验 (1)参数估计：采用非条件最小二乘法进行参数估计,最大迭代次数为10。各备选模型参数显示只有ARIMA(0,1,1)(0,1,1)4模型除常数项外,其他参数均P＜0.05,有统计学意义。根据简洁性原则,将常数项去除,各备选模型结果见表1,仍只有ARIMA(0,1,1)(0,1,1)4模型所有参数具有统计学意义(P＜0.01)。(2)模型拟合优度检验。根据拟合优度结果中AIC和SBC准则,选取两个值均较小的模型为优,结果也显示ARIMA(0,1,1)(0,1,1)4模型的拟合优度较好。AIC值=20.58,SBC值=25.21,SE=0.04,Log-likelihood=3.65。(3)模型残差检验。若残差为白噪声,则意味着所建立的模型已包含了原始序列的所有趋势,从而模型应用于预测是合适的;若残差不是白噪声,说明模型有必要进行改进。对残差序列作自相关和偏相关图(图2和图3),自相关和偏相关函数基本没有突破可信区间,可见残差是随机分布的;同时,结果显示ARIMA(0,1,1)(0,1,1)4模型的Box-Ljung统计量均无统计学意义(Box-Ljung最小值=2.253,P=0.133),可以认为残差序列是白噪声,说明所选模型是恰当的。模型数学表达式为：(1-B)(1-B4)Zt=(1-0.379B)(1-0.652B4)α t,其中Z为季度报告报告发病率的自然对数,B为后移算子,α t为随机干扰。

2.2.4 预测值与实际值比较。采用ARIMA(0,1,1)(0,1,1)4模型,拟合1996年至2008年各季度新涂阳肺结核登记发病率,并对我省2009年新涂阳肺结核的各季度登记发病率进行预测,拟合及预测结果见图1,比较实际值与拟合值和预测值可见模型拟合和预测效果良好,2009年各季度新涂阳肺结核登记发病率的预测值与实际值(表2),相对误差都在10%以下。

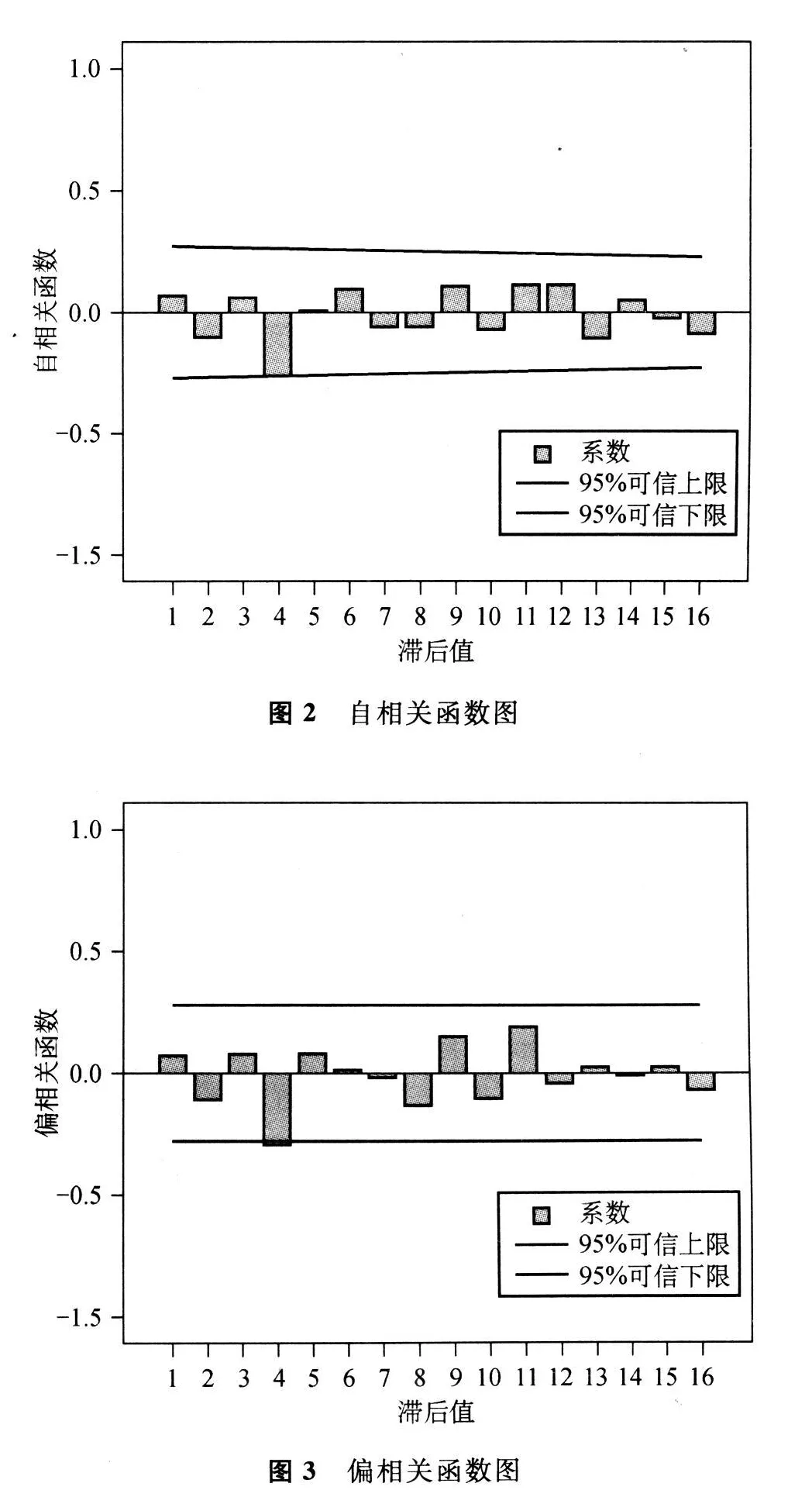
表3 2010—2011年各季度新涂阳肺结核登记报告发病率预测结果

2.2.5 对2010—2011年各季度新涂阳肺结核登记发病率的预测 以1996至2009年各季度新涂阳登记发病率建立模型,对2010—2011年各季度报告登记发病率预测结果(表3)。

3 讨论

众所周知,由于结核病监测受到多种新的因素和干预措施的影响,导致当前结核病疫情监测指标的敏感性和特异性不强,监测信息不能充分反映结核病的实际发病和死亡情况,从而难以及时预测结核病的发病、流行和爆发,不能及时采取有效的应对措施,导致结核病发病和死亡人数的增加,因此结核病的报告发病率预测研究一直备受关注。

曾应用于结核病的流行病学数学模型主要有：Azuma模型、回归模型、指数平滑法、灰色系统预测模型及ARIMA模型等。在众多模型中,Azuma模型应用较为广泛,也曾对于我国结核病流行模式的研究起到一定的指导作用。但随着我国结核病控制工作的进展,结核病三大挑战(流动人口、耐药结核病、HIV合并感染)的出现,应用该模型进行现时的结核病流行预测遇到了一些较为严重的问题。而90年代的回归模型(直线或曲线模型、指数模型、多项式模型)考虑了结核疫情变动的影响因素,保证预测值与观察值的残差最小,不仅可作近期预测,还可作远期预测。但在建立模型时需要样本量足够大,样本服从特定的统计分布规律等比较苛刻的要求,使得其使用受到一定的限制[6-8]。指数平滑法则给予近期观察值以较大的权数并通过对平滑系数的控制以提高预测效果的准确性,但其需要预先凭经验估计出初始平均值及平滑系数,往往要求有较丰富的历史资料来进行多次尝试计算[9-10]。综上所述,这些方法在进行结核病发病预测方面的应用均存在较大的局限性。而本文尝试使用的ARIMA模型是将预测对象随时间推移形成的数据序列视为一个随机序列,利用其依存关系或自相关性表征预测对象发展的延续性,它不需要对时间序列的发展模式作先验假设,方法的本身保证可通过反复识别修正,直至获得满意模型。在预测模型时需要的只是预测对象本身的历史数据,并不要求事先明确所有的影响因素,因此在资料收集的成本上很低;同时,由于ARIMA模型可以将发病的各类影响因素的综合效应统一蕴涵于时间变量中进行分析,短期外推的精确度比线性回归分析更高[11-13]。

本文尝试在考虑其季节因素的情况下,利用1996年至2009年各季度新涂阳结核报告报告发病率,建立的复合季节模型ARIMA(0,1,1)(0,1,1)4,取得的预测结果与实际结果基本一致,各预测值均在95%可信区间内,充分体现了乘积季节模型用于结核病报告发病率的预测是可行的、合理的和可接受的。模型的预测结果可以与常规监测相结合,及时发现报告发病率变化的异常情况,同时可以对采取的结控措施效果进行评价,为结核病的流行预警系统提供技术参数,也可为结核病预测预警模型的建立提供借鉴。

本研究建立的复合季节模型ARIMA(0,1,1)(0,1,1)4,能较好的用于结核病的发病预测,但时间序列模型不是一劳永逸和一成不变的,不能作为永久的预测工具,在实际工作中应该不断的收集积累数据,定期更新模型,才能获得更为准确的预测结果,为结控工作提供更为科学的防控数据。

[1]World Health Organization.Tuberculosis control：Surveillance,Planning,Financing.WHO Report 2005;349.

[2]张文彤.SPSS统计分析教程[M].北京：北京希望电子出版社,2002：250-289.

[3]孙振球.医学统计学[M].北京：人民卫生出版社,2002：461-476.

[4]温亮,徐德忠,林明和.应用时间序列模型预测疟区疟疾发病率[J].第四军医大学学报,2004,25(6)：507-5101.

[5]张蔚,张彦琦,杨旭.时间序列资料ARIMA季节乘积模型及其应用[J].第三军医大学报,2002,24(8)：955-9571.

[6]董选军,贾伟娜.ARIM A时间序列在传染病预测中的比较[J].现代实用医学,2010,(02)：142-143,147,242.

[7]Azuma Y.A simple simulation model of tuberculosis epidemiology for use without large scale computers[J].Bulletin WHO,1975,52：313.

[8]Pilheu JA.Tuberculosis 2000：problems and solutions[J].INT J T UBERC L UNG DIS,1998,2(9)：696-703.

[9]Lalit Kant.BCG Revisited[J].Ind J Tub,2000,47(1)：1-2.

[10]R í os M,Garc í a JM,Sánchez JA,Pérez D.A statistical analysis of the seasonality in pulmonary tuberculosis[J].Eur J Epidemiol,2000,16,(5)：25-27.

[11]Pang SC,Harrison RH,Brearley J,Jegathesan V,Clayton AS：T uberculosis surveillance in immigrants throug h health undertaking s in Western Australia[J].Int J Tuberc Lung Dis 2000,4：232-232.

[12]Nagayama N,Ohmo ri M.Seasonality in various forms of tuberculosis[J].Int J Tuberc Lung Dis,2006,10：1117-1122.

[13]A ntunes JLF,Waldman EA.Tuberculosis in the twentieth century：time-series mortality in Sã o Paulo,Brazil,1900-97[J].Cad Saúde Pública,1999,15：463-476.

Application of time series analysis for the prediction of incidence trend of tuberculosis in Guangdong province

Zhong Qiu,Jiang Li,Zhou Lin,Li Jianwei,Chen Yunhui,Lian Y onge
Anti-tuberculosis Research Institute of Guangdong Province,Guangzhou510630,China

ObjectiveTo utilize the product seasonal model to predict the trend of TB and provide scientific evidence for formulating the related measures of prevention and cure.MethodsThe product seasonal model was combined with ARIMA model and stochastic seasonal model by using the least square principle.ResultsThe ARIMA(0,1,1)(0,1,1)4model was established by the data from 1996 to 2008,and the effectiveness of prediction of this model showed to be good with the actual values in the 95%confidence interval of predicted values.ConclusionThe ARIMA product seasonal model shows effective to predict the incidence of TB in Guangdong province,and the results is in according to the current status of TB,moreover,it could provide information for us to take measures for TB prevention and control.

tuberculosis,pulmonary/prevention and control;tuberculosis,pulmonary/epidemiology;incidence;time;Guangdong province

Zhong Qiu(gdtb@vip.163.com)

钟球(gdtb@vip.163.com)

国家“十一五”重大传染病专项资助(基金编号：2008ZX10003-007)

2010-07-26)

(本文编辑：张晓进)