不完全数据集上的半参组群差异检测

张师超

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

在智能数据分析领域，两数据集间的差异检测是一个应用非常广泛的研究课题.例如，在医学中，要检测一种新药甲能否大批量生产，通常要把其与已有的一些效果很好的旧药(假如药品乙)进行一些差别比较，从而得到新药甲的一些特性，为新药甲的大批量投产或继续改进提供科学依据.检测差别的方法有均值差异检测法和分布函数差异检测法(或分位数差异检测法).在检测过程中，药物甲和乙通常称为对比群(也可以称为对比集或对比总体等)[1].在统计和数据挖掘领域中，均值差异检测、分布函数差异检测或分位数差异检测一般统称为结构差异检测.结构差异检测在统计和数据挖掘方面取得了很大的发展，例如实验数据分析[2]、变化挖掘[3-4]等.

结构差异检测能得到广泛的应用是由于它在数据挖掘领域得到了较大的发展.例如在信息安全方面，检测出垃圾邮件和非垃圾邮件的差异对有效阻止垃圾邮件起着关键的作用[5].组群差异检测已被广泛应用于数据挖掘的各种领域，如多元数据分析[3,5-6]、基于决策树上的变化挖掘[7-9]等.然而，当前组群差异检测面临着以下几个问题：1)数据集经常出现缺失现象.很多工业数据集缺失率高达85%，一些基因数据集的缺失率甚至高达90%以上[10].常见的组群差异检测方法都是假设需处理的数据集是完全数据集(即没有缺失)[11].如果把数据集中缺失的事例去掉，只使用没有缺失的数据集进行差异分析，显然会浪费很多信息，而且使用那些少量没有缺失的事例进行差异检测，肯定不能代表整个数据集的真实情况.2)常见的统计模型经常会对所处理的数据集有无先验知识作出假设.如果对所处理的数据有先验知识，则一般可采用参数方法对数据进行差异检测[12]；如果对所处理的数据没有任何先验知识，则通常采用非参差异检测方法[13].事实上，这2种情形都是极端的，面对2个数据集，用户通常会有些先验知识，此时采用非参差异检测方法是非常合适的[1].3)常见的差异检测方法都是面向2个数据集[14-16].但是，在实际应用中有时需要在一个数据集上进行差异检测，如在一个文本数据集上检测垃圾邮件和非垃圾邮件的差异，或者在一个数据集上检测良性病症和恶性病症的差异，等等.此外，常见的差异检测集中在一个问题的2个对立面，但在实际应用中通常有多类问题，即类标签类别个数多于2类.多类问题中的组群差异问题也能在实际应用中发现，例如如何检测一个气象数据集中类别“晴”与其他类别(如“风”、“多云”、“雨”)的差异.然而，一个数据集上的差异检测，或者多类问题中的差异检测，都还未引起研究者的注意.

本文提出的不完全数据集的差异检测方法为解决以上3个方面的问题提供了理论和技术支撑.首先，采用一种新颖的填充方法对数据集进行填充；其次，在填充得到的数据集上使用经验似然方法，在某个置信水平下推断出2个组群之间的置信区间，对得到的置信区间进行差异检测；再次，讨论和提出了缺失数据填充问题及置信区间的构造；最后，通过实验检测，验证了本算法的优越性.

1 壳填充缺失数据算法

1.1 缺失数据介绍

由于在实际应用中数据缺失的现象非常普遍，因此缺失填充一直是数据挖掘、统计等领域中的一个研究热点.研究者发现，这些数据的缺失会影响从数据集中抽取模式(或规则)的正确性和准确性，从而导致建立错误的数据挖掘模型.

通常，对缺失数据的处理方法有删除、不处理、填充和部分填充四大类.1)删除方法就是将缺失数据所在的事例整个删除，差异分析就在剩下的所有无缺失的事例上进行.这种方法简单但会丢掉很多有用信息.2)不处理方法就是在有缺失数据的数据集中直接学习.这类方法包括贝叶斯网络(Bayesian Network)和人工神经网络(Artificial Neural Networks)等.但此类方法还不十分成熟，算法的复杂度也很高.3)缺失数据填充方法是根据完全数据构造一个模型，然后给缺失数据一个估计值.然而，经常会由于不正确的估计而引入噪音.4)部分填充方法是在最近的文献[17-18]中被提出的，认为没有必要对全部缺失数据进行填充，只需选择其中一部分进行填充，效果会更好.

在研究缺失数据处理问题上，决策方法通常会与数据缺失的机制有关.因此，在对缺失数据进行处理前了解数据缺失的机制和形式十分重要.因此，把数据缺失机制分成以下3类[18]：

1)完全随机缺失(Missing Completely at Random，MCAR).假如条件属性表示为X(X为n维向量)，决策属性为Y.MCAR只说明Y中有缺失值，且与X和Y都无关.这种现象在现实生活中很少见到，一般只会在统计理论中论及.

2)随机缺失(Missing at Random，MAR).缺失数据的可能值仅仅依赖于数据集中不含缺失值的其他变量，也就是说，Y的缺失是与X密切相关的.这种缺失机制简单易行，在机器学习和数据挖掘领域中研究得比较多，通常为默认的缺失机制.本文算法的缺失机制就是这种在机器学习和数据挖掘中经常涉及的MAR缺失机制.

3)非随机缺失(Not Missing at Random，NMAR).缺失数据的可能值不仅依赖于其他变量，还依赖于不完全数据本身.也就是说，对于Y的缺失，除了与X相关外，还与Y本身相关.这种情况在现实生活中很常见，但由于限制条件比较复杂，研究起来比较麻烦，研究成果也不多.

本文提出的填充算法是基于第2种缺失类型(即MAR)和第4种缺失数据处理方法.

1.2 壳近邻填充(SNI)算法

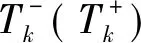
1)首先对数据集进行规范化；

2)for 每个缺失数据z=(X′,Y′){//其中X′为数据的属性，Y′为类标号}；

3)计算和每个完全数据(X,Y)∈D之间的距离dist(X′,X)；

4)选择离z最近的k个完全数据的集合Dz⊆D；

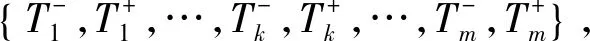
算法1第6步中缺失数据z决策属性的预测值由DS中的完全数据确定.

2 经验似然法构造半参组群差异模型

用F(x)和Gθ0(y)表示2个组群(或称为随机变量)X和Y的分布函数.其中：G已知；F和θ0未知.假设在2个数据集中，其中一个数据集的信息(如G)已知，另外一个数据集的信息未知(如F)，则这种模型被称为半参模型.本文的重点在于使用经验似然方法构造半参模型的均值差异和分布函数差异置信区间.在这种前提条件下，参数和半参模型都不适用.有关经验似然的理论及应用见文献[19-20].

记任意2个组群差异为Δ,则

Eω(x,θ0,Δ)=0.

(1)

式(1)中的ω是一个已知函数形式.根据式(1)，2个组群X和Y的均值差异和分布函数差异可分别定义为：

1)均值差异：μ1=E(x),μ2=E(y)=μ(θ0),Δ=μ2-μ1，其中ω(x,θ0,Δ)=x-μ(θ0)+Δ;

2)分布函数差异：对任意固定的值x0,取p1=F(x0),p2=Gθ0(x0)=p(θ0),Δ=p2-p1，且ω(x,θ0,Δ)=I(x≤x0)-p(θ0)+Δ,其中I(5)是示性函数.

接着，记(x,δx)和y分别为(xi,δxi)和yj，i=1,2,…,m;,j=1,2,…,n.其中

(2)

本文假设随机变量X和Y的缺失机制为MAR，(x,δx)和y是独立的.

表1给出了一个例子，显示本节主要解决的问题.表1中的数据集来自于UCI乳腺癌(Breast Cancer)数据集[21].

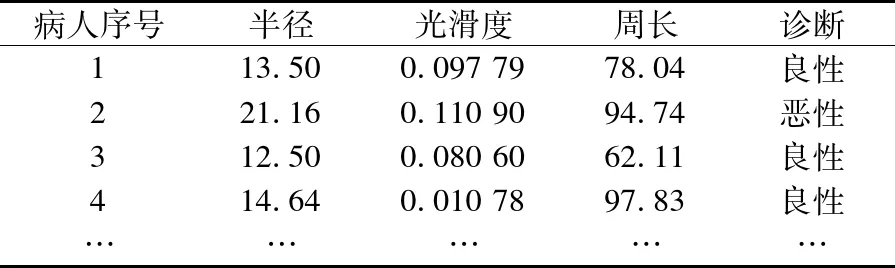
表1 UCI乳腺癌数据集

根据表1可以提出2个问题：1)什么是良性和恶性乳腺癌患者之间的差异；2)已知两者之间的差异，如何衡量什么样的差异值是可信的？

显然，可以通过考察这2个随机变量的一些特性，根据一些简单的统计方法或者数据挖掘方法解决以上2个问题.例如，采用文献[21-23]的方法可以解决第1个问题.对含有缺失数据的随机变量的差异(即第2个问题)，本文采用经验似然的方法构建2个随机变量的置信区间(在某显著性水平α下).

(3)

2.1 对差异Δ构造置信区间

本节构造的组群差异Δ置信区间的经验似然统计的渐进分布可以被证明是一个加权的卡方分布 (详见定理 1 ).首先，半参似然函数定义为

(4)

(5)

式(5)中:

R(Δ,θ)=

应用拉格朗日乘子法得到

(6)

λ(θ)由下式决定：

(7)

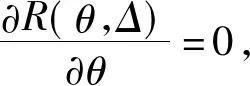
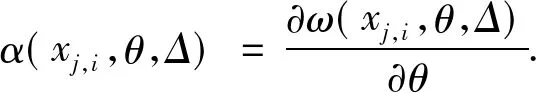
1)θ0∈Ω及Ω均为开区间;

2)A={y|gθ(y)>0}完全独立于θ;

3)∀y∈A,gθ(y)关于θ的三次微分均存在；

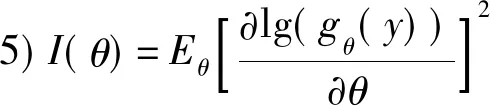
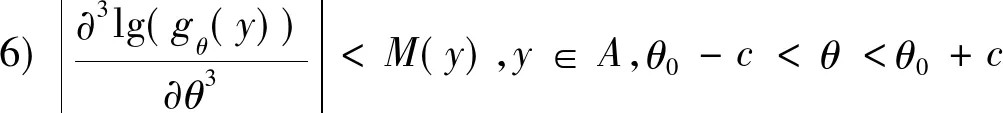
定理1假设条件1)～8)都满足，则式(6)中的θ存在一个解，此解使R(Δ,θ)局部最小,且

(8)

式(8)中：

i=1,2,…,n;

β0=E[α(x,θ0,Δ)];

2.2 基于经验似然的Δ置信区间

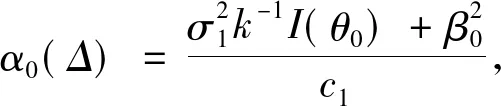
假设tα满足P(χ2≤tα)=1-α，根据定理1, 关于Δ的基于经验似然的置信区间渐进收敛于1-α为

(9)

式(9)可以直接对Δ进行假设检验.例如，如果H0:Δ=Δ0,H1:Δ≠Δ0,那么,首先根据式(9)为Δ构建置信区间，然后检测初始值Δ0是否在得到的区间内.如果Δ0在区间内，则接受假设;否则，拒绝假设.

使用经验似然方法构建置信区间的算法(算法2)如下：

Input:数据集x,y

Output:均值和分布函数的置信区间

1)Begin

2)Δ=(E(y)-E(x))-a

3)MeanLeft=FindEndPoint(left,Δ)

4)Δ=(E(y)-E(x))+a

5)MeanRight=FindEndPoint(right,Δ)

6)Δ=(DFG(X0)-DFF(X0))-b

7)DFLeft=FindEndPoint(left,Δ)

8)Δ=(DFG(X0)-DFF(X0))+b

9)DFRight=FindEndPoint(right,Δ)

10)Output CIs:(MeanLeft,MeanRight),(DFLeft,DFRight)

Sub procedure FindEndPoint(direction,Δ)

11)If (directin=left) step=1e-2 else step=-1e-2

12)While (1)

13)(λ,θ)←the roots of eq. (6) and (7)

14)compute (8) based on (λ,θ) and datasetx,y

15)if ((9) is satisfied) returnΔelseΔ=Δ+step

End sub

(note thata,bare random selected constants with respect toΔ)

3 实验分析

为了检测算法的优越性，把本文算法(记为SNIEL)同常见的构造置信区间算法——解鞋带重抽样算法[24](Bootstrap re-sampling算法，本文记为BOOT)及使用最近邻填充缺失数据算法2构建置信区间方法(记为NNEL)在UCI真实数据集上进行比较，评价指标为构造出的置信区间的长度和真实值在置信区间中的覆盖率.置信区间的长度越短且覆盖率越大，说明构造出的置信区间效果越好.首先，对有缺失的数据集(2个组群均含有相同比例的缺失数据)，算法SNIEL和算法BOOT均使用算法1填充缺失数据，NNEL算法使用k-近邻算法填充缺失数据，2种填充算法都需要设置参数k, 在实验中统一取k=5.在完全的数据集中，SNIEL和NNEL使用算法2构建均值和分布函数的置信区间，BOOT使用解鞋带重抽样算法[14]构建置信区间.对比实验有3组，分别为单一组群并且无类标签的对比实验；2个组群类标签为两类的对比实验；2个组群类标签为多类的对比实验.要注意的是：1)实验过程中的置信水平统一设为1-α，其中α=0.05；2)本文实验数据集均为无缺失数据集(为了跟原始数据进行比较)，实验过程中统一使用MAR方法,随机使20%的事例含有缺失数据，称其缺失率为20%.

3.1 单一组群对比实验

单一组群实验是为了检测2种方法(经验似然法和解鞋带重抽样法)构建的置信区间是否为紧(即置信区间长度较短).若置信区间的长度趋于0，则说明在这个组群里抽样出来的2个样本服从同一分布.在实际应用或者理论研究中，都可以利用这个方法检测设计的抽样算法是否有效.

实验数据集为abalone 数据集，共有4 177 事例，每个事例有9个属性.实验设计中，首先随机把abalone 数据集分成2个部分:一个部分含有2 581个事例,记为D1;另一部分为 1 596 事例,记为D2.这里只对第3，5和6个属性建立置信区间.实验样本为200，实验次数1 000次，记录每次实验的原始均值和分布函数，最终结果为1 000次的平均值.由于实验在一个数据集中进行，因此2个组群的差异Δ理论上应为0.

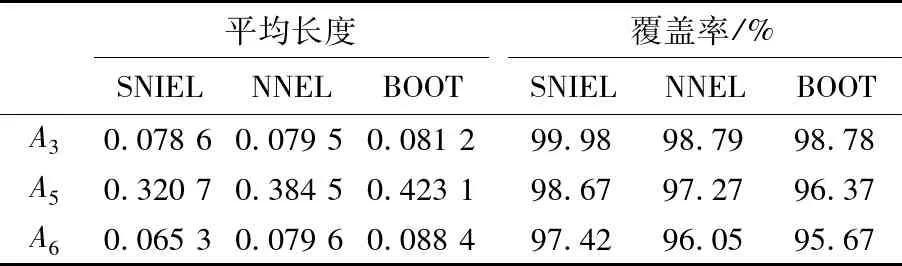
表2 均值置信区间平均长度及覆盖率比较

表3 分布函数置信区间平均长度及覆盖率比较

由表2及表3说明：3种算法构造的均值区间的长度都接近于0，且覆盖率均超过了95%，说明3种方法都是有效的.但对比两种使用算法2构造置信区间的方法，算法BOOT无论在分布函数还是均值置信区间上都处于劣势，说明构造置信区间算法优于解鞋带重抽样法.对比2种使用经验似然构造置信区间的算法发现,算法SNIEL的各评价指标均优于算法NNEL，这是因为SNIEL算法使用了壳近邻填充算法，而NNEL使用的是近邻填充算法.因此，壳近邻填充算法在构造不完全组群置信区间方面要优于最近邻算法.

3.2 两类实验

单个组群差异检测可显示一个组群中的2个样本是否来自同一个分布，2类组群差异检测则可以显示2个组群(即使是具有不同分布，甚至只知道其中1个组群分布情况)的差异情况.

实验选取数据集Wisconsin breast cancer dataset，共有569个事例和32个属性.类属性有2个类，其中良性患者类有357个事例，恶性患者有212个.只对第4，15和27个属性进行实验.结果如表4和表5所示.在2个组群的比较实验中，用经验似然方法估计置信区间的算法无论是置信区间的平均长度或真实值在置信区间的覆盖率都要比用解鞋带重抽样构造置信区间的算法好.

表4 均值置信区间平均长度及覆盖率比较

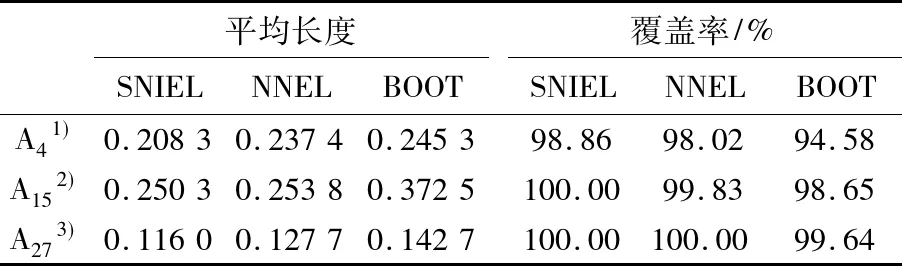
表5 分布函数置信区间平均长度及覆盖率比较

3.3 多类实验

现实数据集的类标签经常含有多类情况.例如，一个有关气象数据集的类标签有“晴”、“多云”、“风”和“下雨”.若需估计一个数据集中含有多类标签间的差异，则可以先对这些类标签做组合(如“晴”跟“多云”、“晴”跟“风”、“晴”跟“下雨”等各做一个组合)，然后再检测这些组合的差异性.但是，此方法至少含有2个问题：1)这样的组合势必加大计算量；2)如果只分析2个类别之间的差异，而不考虑其他类标签的组合(如只分析“晴”跟“风”的差异，不考虑“晴”跟“多云”及“晴”跟“下雨”等的组合)，显然是不合理的.本文把“晴”作为一类，其他作为一类，就可以解决以上2个问题.实验数据集为Wine数据集(有3个类)、Iris数据集(3个类)和Yeast数据集(10个类).结果如表6和表7所示.实验结果与表2～表5的一样，唯一不同的是，算法BOOT在多类问题中不太稳定，这可能是由于解鞋带重抽样方法的不稳定性造成的.

表6 均值置信区间平均长度及覆盖率比较

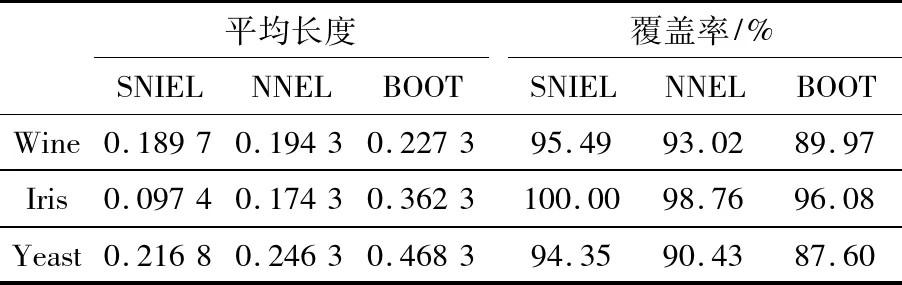
表7 分布函数置信区间平均长度及覆盖率比较

4 结 论

由于理论保证，经验似然方法在3种实验比较中都优于解鞋带重抽样方法.这是因为,虽然经验似然方法的实验结果显示了较短的置信区间,但却具有更高的覆盖率.

参考文献：

[1]Huang Huijing,Qin Yongsong,Zhu Xiaofeng,et al.Difference Detection between Two Contrast Sets[M].Berlin:Springer,2006:481-490.

[2]Bay S D,Pazzani M J.Characterizing Model Errors and Differences[C]// Proceedings of the Seventeenth International Conference on Machine Learning.New York:ACM,2000:49-56.

[3]Bay S D,Pazzani M J.Detecting Change in Categorical Data:Mining Contrast Sets[C]// Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM,1999:302-306.

[4]Au W H,Chan K C C.Mining changes in association rules:a fuzzy approach[J].Fuzzy Sets and Systems,2005,149(1):87-104.

[5]Bay S D,Pazzani M J.Detecting Group Differences:Mining Contrast Sets[J].Data Mining and Knowledge Discovery,2001,5(3):213-246.

[6]Webb G I,Butler S M,Newlands D A.On detecting differences between groups[C]//Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM,2003:256-265.

[7]Cong Gao,Liu Bing.Speed-up Iterative Frequent Itemset Mining with Constraint Changes[C]//Proceedings of the International Conference on Data Mining.New York:IEEE,2002:107-114.

[8]Liu Bing,Hsu W,Han H S,et al.Mining Changes for Real-Life Applications[M].Berlin:Springer,2000:337-346.

[9]Wang Ke,Zhou Senqiang,Fu C A,et al.Mining Changes of Classification by Correspondence Tracing[C]//SIAMDM ’03,SIAM International Conference on Data Mining.San Francisco:SIAM,2003.

[10]Lakshminarayan K,Harp S A,Samad T.Imputation of missing data in industrial databases[J].Applied Intelligence,1999,11(3):259-275.

[11]Zhang Shichao.Detecting Differences between Contrast Groups[J].IEEE Transactions on Information Technology in Biomedicine,2008,12(6):739-745.

[12]Jing Bingyi.Two-sample empirical likelihood method[J].Statistics and Probability Letters,1995,24(4):315-319.

[13]Qin Yongsong,Zhang Shichao.Empirical Likelihood Confidence Intervals for Differences between Two Datasets with Missing Data[J].Pattern Recognition Letters,2008,29(6):803-812.

[14]Hall P,Martin M.On the bootstrap and two-sample problems[J].Austral J Statist,1988,30A(1):179-192.

[15]Wang Qihua,Rao J N K.Empirical likelihood-based inference in linear models with missing data[J].Scand J Statist,2002,29(3):563-576.

[16]Wang Qihua,Rao J N K.Empirical likelihood-based inference under imputation for missing response data[J].Ann Statist,2002,30(3):896-924.

[17]Zhang Shichao,Member S,IEEE.Parimputation:From imputation and null-imputation to partially imputation[J].IEEE Intelligent Informatics Bulletin,2008,9(1):32-38.

[18]Zhang Shichao.Shell-Neighbor method and its application in missing data imputation[EB/OL].(2010-02-20)[2010-02-28].http://www.springerlink.com/content/666244u672v6171v/.

[19]Owen A.Empirical likelihood[M].New York:Chapman & Hall,2001.

[20]Owen A.Data Squashing by Empirical Likelihood[J].Data Mining and Knowledge Discovery,2003,7(1):101-113.

[21]Blake C,Merz C.UCI Repository of machine learning database[ED/OL].[2009-08-21].http://www.ics.uci.edu/～mlearn/MLResoesitory.html.

[22]Cho Y B,Cho Y H,Kim S H.Mining changes in customer buying behavior for collaborative recommendations[J].Expert Systems with Applications,2005,28(2):359-369.

[23]Ying A T T,Murphy G C,Raymond T N,et al.Predicting Source Code Changes by Mining Change History[J].IEEE Trans Software Eng,2004,30(9):574-586.

[24]Little R,Rubin D.Statistical analysis with missing data[M].2nd ed.New York:John Wiley & Sons,2002.