改进的以x(1)(n)为初始条件的GM模型

尹方平

（广东机电职业技术学院，广州 510515）

0 引言

影响GM（1,1）模型预测精度的原因有两个，其一是模型中背景值的构造方法；其二是预测公式中初值的选取。经典GM(1,1)模型的初始值选取问题，在原有初始值选取的基础上，出现了多种改进方法的讨论[1-7]。本文对灰色GM（1,1）模型的预测精度进行了分析，提出了一种修正初值法来提高模型的精度，对以x(1)(n)为初始条件的GM模型进行了改进，使所建的模型的精度大为提高，最后通过具体的实例验证了模型的实用性与可靠性。

1 以x(1)(n)为初始条件的GM模型

以x(1)(n)为初始条件的GM模型是根据新信息优先原理和最少信息原理提出的灰色GM模型的一种改进的方法。

定义1 称方程x(0)(k)+az(1)(k)=b为灰色微分方程，此模型为 GM（1,1）模型。

其中a和b为待确定的常数。其中a为发展系数，它的大小及符号反映了x(0)(k)及x(1)(k)的发展态势。如果a为负，那么态势是增长的，a的绝对值越大，增长越快；如果a为正，那么态势是减弱的，a的绝对值越大，衰减越快。b为系统的灰作用量，它是从背景值挖掘出来的数据，反映数据变化的关系。

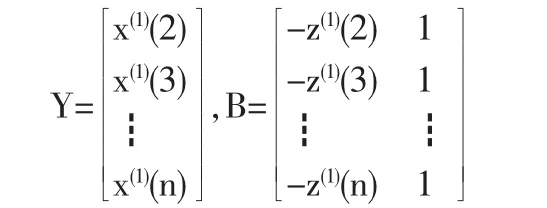
则GM(1,1)模型x(0)(k)+az(1)(k)=b的最小二乘估计参数列满足

由定理1及白化方程的离散解不难得：

以x(1)(t)为初始条件的GM模型白化方程+ax(1)=b的时间响应函数为：

从上述模型可以看出，GM（1，1）模型的拟合和预测精度不但跟常数a,b有关，还跟x(1)(n)的取值有关。因此合理的选择初值对于提高模型的预测精度有着重要的作用。本文在最小化指定指标函数的情况下，提出了改进x(1)(n)初值的方法。

2 改进的以x(1)(n)为初始条件的GM模型

由于初始条件x(1)(n)是由原始序列X(0)累加生成的，原始序列信息通过x(1)(n)都可以得到充分反映，因此把它作为GM模型的初始条件可以克服GM建模与x(1)(1)的弊端。基于新信息优先原理以及合理的初值选择原理的应用，本文假设模型的初值取αx(1)(1)，并把该初值代入

我们采用最小二乘原则的方法，建立一个无约束优化模型，求解x^(1)(k)和x^(1)(k)误差平方和最小，也就是求解优化问题：minJ

为了求出指标函数值最小时的待辨识参数α，先用如下梯度法求取：

3 实例与讨论

发电量是衡量一个国家发展水平和人民生活水平的一个重要指标，所以建立发电量模型并预测其未来的发展趋势具有重要的现实意义。现用本文提出的方法建立1989-1999年我国上海市的发电量《上海统计年鉴-2002》的GM（1，1）模型[8]，并预测2000-2002年的上海市发电量。

用传统的GM（1，1）方法建立的模型为：

x^(1)(k)=4927.7le0.058366(k-1)-4652.96,k≥1

表1 模型值比较表 (单位：kw:h)

x^(0)(k+1)=279.49e0.058366,k≥1

x^(0)(k)=278.33

用αx(0)(1)以为初始条件的GM改进模型Ⅰ为：

其中 α=0.99493。

用以αx(1)(n)为初始条件的GM改进模型Ⅱ为：

计算结果如表1所示：

4 小结

（1）本文对 GM（1，1）模型的预测精度进行了分析，认为初值x(1)(n)的选取对模型的精度有重要的影响，提出了一种修正初值法来提高模型的精度，对以x(1)(n)为初始条件的GM（1，1）模型进行了改进。该方法保留了GM（1，1）模型建模计算简便和易于应用的优点，不存在复杂的计算。

（2）从实例分析上看，该方法能得到比原 GM（1，1）模型和以αx(1)(n)为初始条件的GM改进模型更高的精度和适应性，因而具有重要的理论价值和实践意义。

[1]谭冠军.GM（1,1）模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践,2000,20（5）.

[2]宋中民,邓聚龙.反向累加生成及灰色GOM（1,1）模型[J].系统工程,2001,19(1).

[3]罗党,刘思峰,党耀国.灰色模型 GM(1,1)优化[J].中国工程科学,2003,5(8).

[4]Ming Feng Yeh,Hung Ching Lu.A New Modified Grey Model[J].The Journal of Grey System.1996,8(3).

[5]Deng Ju Long,Solution of Grey Differential Equation for in matrix Train[J].The Journal of Grey System.2002,14(1).

[6]王义闹,刘光珍,刘开第.GM（1,1）模型的一种逐步优化直接建模法[J].系统工程理论与实践,2000,20(9).

[7]党耀国,刘思峰,刘斌.以为初始条件的GM模型[J].中国管理科学,2005,13(1).

[8]李俊峰,戴文战.GM(1,1)改进模型的研究及在上海市发电量建模中的应用[J].系统工程理论与实践,2005,3(3).