拟合优度检验统计量的设定方法
2010-05-22刘黎明
王 重,刘黎明
(首都经济贸易大学 统计学院,北京 100026)
1 问题提出
构建经济计量模型研究经济问题,首先确定研究对象,然后分析研究对象,确定影响研究对象的变量;根据变量之间的相互关系,确定经济计量模型的结构解析式;而后利用搜集到的数据估计模型未知参数;最后,对模型进行检验,模型通过检验后,就可以利用经济计量模型解释经济现象。
经济计量模型的变量选取,模型结构解析式的确定需要经济理论和先验的经验研究,模型检验是经济计量模型能够解释经济现象的保证。经典线性模型中的检验中有拟合优度检验、模型系数检验、模型总体检验。三个检验方法中,拟合优度检验和模型总体检验主要检验模型的拟合程度,模型通过拟合优度检验,才可以进行系数检验。
2 模型检验存在的问题
拟合优度检验最早由英国统计学家K·皮尔逊提出,皮尔逊明确指出统计学不仅仅研究样本,而是根据样本对总体进行推断。模型检验是构建模型过程中重要的一环。经典的计量经济学通过构造检验统计量进行模型假设检验。模型拟合优度检验,模型假设和检验统计量的构造以数理统计知识为基础。经典的模型检验,需要检验模型参数,并且还需检验模型总体显著性。
回归拟合度评价统计量:

拟合优度检验用于检验回归模型的拟合程度,拟合优度检验是模型系数检验的基础,在模型通过拟合优度检验后,才可进行模型系数检验。统计量检验模型的拟合程度被证明存在问题,Anscombe在1973年给出了四组著名数据,证明了R2不能充分检验回归模型拟合情况,统计量R2无法充分反映模型的拟合程度,使用统计量R2无法有效的检验模型的拟合程度。
表1中数据被分为四组,G1(x1,y1),G2(x2,y2),G3(x3,y3),G4(x2,y4),对这四组数据进行一元线性回归。设定模型:
y=β0+β1x+ε
采用最小二乘法估计模型,得到模型参数和模型的主要统计量。

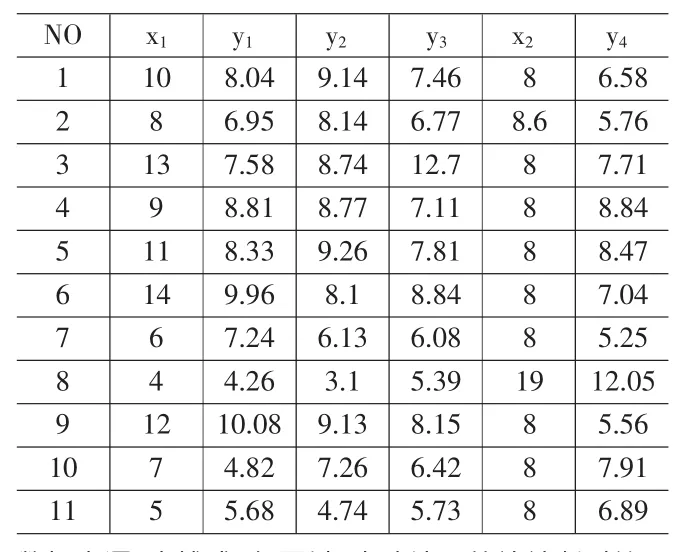
表1 Anscombe数据

表2 各数据组模型统计量

表3 各组数据估计模型残差表
从表2可以看出,数据组G1,G2,G3的模型参数估计值和模型的拟合优度检验统计量基本一致,0.7。拟合优度检验统计量的值不是很高,但还是不能否认R2本身存在的问题。四组数据拟合模型,我们得到相似的回归方程,但数据却存在很大差别。
如图1所示,模型y=3+0.5x对于数据组G1与G3的拟合优度检验统计量为0.7,基本可以拟合,但是对于数据组G2,拟合优度检验统计量也是0.7,拟合效果就要差很多,因此单独利用R2检验模型的拟合优度是欠妥的。
拟合优度检验统计量R2不能够很好检验模型的拟合情况,这与统计量 R2的构造有关。 R2中包含有(Y-)与(Y^-),获得自变量数值的方式不同,也就具有不同的含义。自变量Y数据来源有两种方式,第一类是通过可重复实验获得的数据。例如:在常温,常压状态下,某工厂测量合金A的强度,对合金A施加100000牛冲击力,实验3万次,合金A的3万次实验的数据记录下来,测算合金A的强度。合金A的强度为研究对象,构造模型y=p×s+ε,利用数理方法,估计合金A的强度。可重复实验得到数据,可以保证实验条件的稳定性,把外界的干扰控制到最低。在实验中,可以精确的控制每一个Y影响研究对象的变量。本例中,可以精确的控制温度、压强、冲击力。此时R2的就是试验观测数值得均值,并且与每一个十分接近,此时R2作为检验模型的拟合程度不是很合适。第二类是不可重复性试验的时间序列数据。在经济问题的研究中,我们得到大量无法重复的时间序列数据。例如:为了研究某地区的消费规律,根据统计资料查到该地区人均收入、人均储蓄和人均消费1981年到2002年的年度数据,通过对数据的分析,估计人均收入、人均储蓄对人均消费的影响程度。人均消费作为研究对象,记录纵向年度不同时刻变量的值,利用这些统计数据构建模型研究人均收入、人均储蓄与人均消费的关系。构建面板数据模型,存在个自变量,研究面板数据研究自变量与因变量的关系,面板数据收集时,n个自变量与因变量同时变化,这时就变成自变量Y的算术平均值,并不能保证与每一个Y十分接近,那么借助R2与对模型进行拟合的检验就可能出现Anscombe所论证的问题。
3 拟合优度检验统计量
检验模型的拟合优度可以构建新的统计量,拟合优度检验的统计量可以设定为:

模型的拟合优度检验是检验设定模型的拟合程度,检验拟合优度的统计量应该实际反映模型的拟合水平。检验模型的拟合程度,残差是良好的统计量,使用残差必须消除残差的量纲影响,统计量αi消除量纲影响,残差表示估计值与真实值之间的差别,残差除以真实值表示残差占真实值的比率。
模型因变量与自变量关系稳定,确定模型变量之间的函数关系,yi服从正态分布。模型因变量服从正态分布,不可采用拟合优度X2统计量检验模型拟合优度。估计模型函数关系确定后,构造模型的拟合优度检验X2统计量
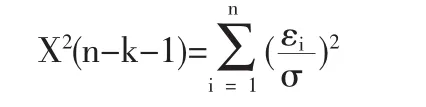
模型假设 εi服从独立正态分布,εi~N(0,σ2),计算 X2统计量,必须知道残差的方差 σ 的值,在 εi~N(0,σ2)的前提假设条件下,采用无偏统计量σ^2代替,代入X2统计量,得到X2(n-k-1)=n-k-1,因此X2统计量无法作为模型的拟合优度检验统计量。模型总体检验使用F统计量,F统计量构造中含有R2,R2检验拟合优度存在不足,那么使用F统计量检验模型的拟合优度也是存在问题的,因此使用统计量β检验模型拟合优度是可行。
如果模型每一个ai都是小于0.95,那么可以认定模型拟合程度高,在上例中,数据组G3的统计量R2受异常点的影响,R2值不理想,但模型的拟合程度还是很高的。统计量β由所有因变量的残差与真实值比值绝对值的平均数,表示模型总体的拟合情况。数据组 G1(x1,y1),G2(x2,y2),G3(x3,y3),G4(x2,y4)的检验结果见表3,表4。

表4 各模型拟合检验统计量表
从检验结果来看,模型y=β0+β1x+ε对四组数据模拟,G3(x1,y3)的检验值最小,统计量β=0.07,若假设β<0.1就可以接受模型,那么就可以利用模型对数据G3(x1,y3)进行经济分析,数据组 G1(x1,y1),G2(x2,y2),G4(x2,y4)的模型需要进行修正,仅当 G1、G2、G3 的模型统计量 βi<0.1,才可借助模型进行经济分析。
4 结论
检验模型拟合优度,统计量R2构造存在问题,不能很好地反映模型的实际拟合程度,而统计量β从模型本身出发,可以准确的辨别模型的拟合情况。实际研究中,根据研究对象的不同,设定不同精度,得到拟合数据的最佳模型,分析经济问题。
[1]Anscombe,F.J,et al.Graphs in Statistical Analysis[J].Am.Statist,1973,27.
[2]Braun,H,et al.A Simple Method for Testing Goodness of Fit in the Presence of Nuisance Parameters[J].R.Staat.Soc.1980,42.
[3]Larntz,K,Small-sample Comparisons of Exact levels for Goodness of Fit Statistics[J].J.Am.Stat.Assoc,1978,73.
[4]Khan,Azizur Rahman,Carl Riskin,et al. Growth and Distribution of Household Income in China between 1995 and 2002[C].Working Paper,2008.
[5]Tigor,Robert L.W.Arthur Lewis and the Birth of Development Economics[M].Princeton:Princeton University Press,2006.
[6]Christopher M,Fleming Robert R,et al.Single-species Versus Multiple-species Models:the Economic Implications[J].Ecol Model,2003,170.
[7]Fafchamps,M Minten,et al.Returns to Social Network Capital Among Traders[J].Oxford Economic,2002,542.
[8]韦博成,鲁国斌,史建清等.统计诊断引论(第一版)[M].南京:东南大学出版社,1991.
[9]谢识予,朱宏鑫.高级计量经济学(第一版)[M].上海:复旦大学出版社,2005.
[10]李子奈,潘文卿.计量经济学(第二版)[M].北京:高等教育出版社,2005.
