一种多变量线性回归模型的异方差检验方法

郑红艳，夏乐天

（河海大学 理学院，南京 210098）

1 异方差模型

经典线性回归模型的一个重要假设就是回归方程误差项εi具有相同的方差，也称方差齐性，其经典线性回归模型可以表示为

假设有 n 组观察值(yi，xi2，xi3，…，xik)，i=1，2，…，n，则(1)式可表示为

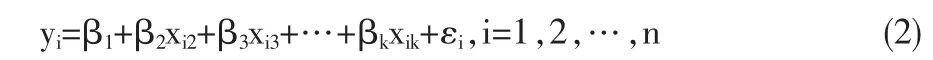
用矩阵可表示为

其中Y是被解释变量观察值的n维向量，X是解释变量的n×p矩阵，β为p维的未知系数向量，ε是n维的随机误差项向量。

如果在回归模型(2)中，不管x取什么值，εi的方差都是同一常数，我们就说εi具有同方差性（也称方差齐性）。然而，在现实中，人们发现有不少现象与方差齐性相违背。当方差齐性假定不满足，也就是说误差项εi的方差不等于一个常数，即

则称误差项εi具有异方差性。在模型(3)中，除误差项具有异方差性外，其它基本假设都能满足，则称这种模型为异方差的线性回归模型，简称异方差模型[1-2]。

特别是当讨论横截面数据时，异方差性通常是不可避免的。例如，当讨论公司利润与若干解释变量的线性回归模型时，大规模公司的利润显然比小规模公司的利润有更大的波动性，又如，当研究家庭收入(解释变量)和储蓄(因变量)之间的线性回归关系时，由于高收入家庭除了必要的家庭支出外剩余较多，随意支配部分较大，因而，他们储蓄多少的随意性也较大，即储蓄额的差异较大。

如果对异方差模型进行最小二乘估计(OLS估计)，就会产生严重的错误[3]：参数估计量的方差不具有最小方差性；估计与预测的精度降低。因此，异方差性的检验具有重要的经济意义。

2 异方差性的检验

常用的检验异方差的方法有很多。如果在同一条件下，存在重复试验或重复观察的话，统计学家已经提出了不少方差齐性的检验方法。譬如，巴特列特(Bartlett)检验等[4]。但是，在经济问题中，很少存在这种数据，为此，经济计量学家又提出了许多不同的方法，譬如图示法、斯皮尔曼(Spearman)的秩相关系数检验法、戈德菲尔德-匡特(Goldfeld-Quandt)检验法等等，文献[4]甚至还给出了一种不依赖于残差的异方差检验方法。其中，戈德菲尔德-匡特检验法（简称“G-Q检验法”）是最为常用的方法之一。由于戈德菲尔德-匡特检验方法只适用于一个自变量[3]，因此，本文给出了一种适用于多变量的异方差检验法，该法实质上就是一种推广的G-Q检验法，它只需要对样本数据进行若干次单变量G-Q检验，即可得到是否有“方差齐性”的推断。

2.1 单变量戈德菲尔德-匡特(Goldfeld-Quandt)检验

戈德菲尔德-匡特检验，简称G-Q检验，这种检验适用于大样本。这种检验要求随机项εi服从正态分布且εi无序列相关。检验的方法以F检验为基础，它把随机样本分为三段，去掉中间一段。假定低样本组的数据具有同方差性，设方差为，高样本组的数据也具有同方差性，设方差为。然后比较高样本组与低样本组的方差是否相同。若方差相同，说明数据中不存在异方差；若方差不同，说明数据中存在异方差。

设 x为所考虑的解释变量，检验原假设 H0：，备择假设 H1：。

G-Q检验的步骤为：

(1)把观察值按照解释变量x由小到大的顺序排列，对应的被解释变量与解释变量的对应关系不变。

(2)略去c个中心观察值，c的大小约为样本容量n的四分之一到三分之一，为了计算上的方便最好使n-c为偶数。

(3)剩下n-c个样本观察值分为大小相等的两个样本，第一个样本包含的观察值相应于解释变量x的较小部分第二个样本包含的观察值相应于解释变量x的较大部分。

(4)应用普通最小二乘法对每个样本分别进行回归，并计算出相应的残差平方和ESS1和ESS2。

(5)选择统计量

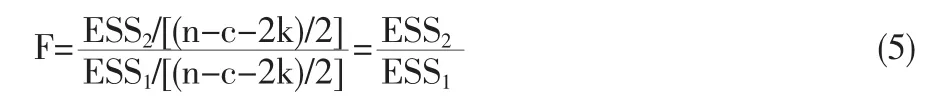
在H0为真时，F服从自由度为r1=(n-c-2k)/2，r2=(n-c-2k)/2的F分布。这里的k为回归模型中参数的个数。如果选定显著性水平α，那么可利用F分布的临界值Fα(上侧α分位点)进行显著性检验。当F＞Fα时，拒绝原假设H0，认为存在异方差性，当 F≤Fα时，接受原假设 H0，认为 εi方差齐性。

G-Q检验法对单个解释变量来说，是一种方便、快捷检测异方差存在性的方法。但对于多个解释变量，这种方法在使用上有一定的困难。因此，本文对这种方法作进一步的推广。

2.2 适用于多变量的推广的G-Q检验

由于多元线性回归模型的异方差检验实际上可以转化为，对每个解释变量对应被解释变量的一元线性回归模型的异方差检验，若所有一元线性回归模型都不存在异方差，则可近似认为多元线性回归模型或数据不存在异方差，反之，若出现有一个一元线性回归模型存在异方差，则就认为原多元线性回归模型或数据存在异方差。从而我们可以得到一种针对多变量的推广的G-Q检验方法，即对每一个解释变量采用单变量的G-Q检验方法，检验是否存在异方差。若其中有一个一元线性回归模型存在异方差，则就认为原多元线性回归模型或数据存在异方差。具体步骤如下：

(1)把观察值按照解释变量xi(i=1，2，…，n)由小到大的顺序排列，对应的被解释变量与解释变量的对应关系不变。

(2)略去c个中心观察值，c的大小约为样本容量n的四分之一到三分之一，为了计算上的方便最好使n-c为偶数。

(3)剩下n-c个样本观察值分为大小相等的两个样本，第一个样本包含的观察值相应于解释变量xi的较小部分第二个样本包含的观察值相应于解释变量xi的较大部分。

(4)应用普通最小二乘法对每个样本分别进行回归，并计算出相应的残差平方和ESS1i和ESS2i。

(5)选择统计量

在 H0为真时，Fi(i=1，2，…，n)服从自由度为 r1=(n-c-2k)/2，r2=(n-c-2k)/2的F分布。这里的k为回归模型中参数的个数。如果选定显著性水平α，那么可利用F分布的临界值Fα(上α侧分位点)进行显著性检验。当存在Fi＞Fα时，拒绝原假设 H0，认为存在异方差性，当所有 Fi≤Fα(i=1，2，…，n)时，接受原假设H0，认为εi方差齐性。

表1 31个地区城镇居民家庭全年人均经济数据

3 应用举例

下面，我们以一个实例来验证以上方法的可行性和有效性。考虑消费性支出(y)与收入(x1)、食品支出(x2)及娱乐教育文化服务支出(x3)的关系模型。收集2007年我国31个地区的城镇居民家庭平均每人全年的消费性支出包括食品支出及娱乐教育文化服务支出，各地区城镇居民平均每人全年家庭实际收入数据（单位：千元）如表1所示。

首先我们采用文献[3]给出的方法，经过计算，可知表1中数据不存在异方差，这似乎有悖经济学方面的理论。下面我们使用本文提出的方法，再次对数据进行检验。

对解释变量x1按照从小到大的顺序进行排序，对应的被解释变量与解释变量的对应关系不变。去掉排序后的中间9组数据，即c=9，n=31，k=2，就可得到两个样本，其样本个数都是11，且第一个样本包含的观察值相应于解释变量x1的较小部分第二个样本包含的观察值相应于解释变量x1的较大部分。

对前11组数据进行回归得到

其残差平方和为1.2383。

对后11组数据进行回归得到

其残差平方和为5.7738。

检验统计量为

类似地，我们对解释变量x2和x3进行以上处理，得到检验统计量 F2=4.87，F3=4.12。

查 F 分布表，得临界值 F0.05(9，9)=3.18。 由于 Fi＞3.18，i=1，2，3，所以接受备择假设，即认为数据中存在异方差。

事实上，用本文中所给的方法对文献[3]中的例子进行检验，也可以得到相同的结论。

4 结语

在某些有关计量经济的回归模型中，假设误差项具有方差齐性是不合理的。异方差的情况在截面数据中常常出现.。对这种异方差模型进行最小二乘估计，会产生严重的错误，因此研究异方差的检验方法具有重要意义。

由于戈德菲尔德-匡特检验方法只适用于一个自变量，因此，本文给出针对多变量的G-Q检验方法，即对每个解释变量进行异方差检验，从而判断原模型的异方差性。通过实例我们还看出，本文所给的方法比文献[3]中的方法适用更广，也更简便易行，即只要进行若干次的单变量G-Q检验就行了。

当然，异方差的检验除了上述叙述的方法外，还有很多的方法。文献[3]给出了一种基于样本主成分的推广的G-Q检验方法，文献[4]则给出了一种基于分组的异方差检验方法。如何根据实际情况选择最好的检验方法是值得研究的。当然，最优检验方法的选择不是固定的，George G.Jude[7]等人认为，最优检验方法的选择还依赖于人们对可能的异方差形式的先验认识。

[1]White H.A.Heteroscedasticity-Consistent Covariance Matrix Estimator and Direct Test for Heteroscedasticity[J].Econometrica,1980,(48).

[2]Park R.E.Estimation With Heteroscedastic Error Terms[J].E-conometrica,1966,(34).

[3]龚秀芳.戈德菲尔德-匡特检验的推广[J].数理统计与管理，2005，24.

[4]张荷观.基于分组的异方差检验和两阶段估计[J].数量经济技术经济研究，2006，(1).

[5]白雪梅.异方差性的检验方法及评述[J].东北财经大学学报，2002，(11).

[6]王正林等.精通MATLAB科学计算[M].北京：电子工业出版社，2007.

[7]姜诗章，王锦功.计量经济学教程[M].吉林：吉林大学出版社，1989.