联合生存概率准则下的最优再保险研究

李 凯

（中央财经大学 中国精算研究院，北京 100081）

0 引言

再保险精算研究中，最优再保险一直备受关注，最早由Pesonen[1]提出使原保险人风险的波动（即方差）达到最小作为最优准则，求得最优再保险的形式。Gajek[2],Kaluszka[3]则以原保险人方差最小作为最优准则，得到了最优再保险的统一形式。Young[4,5]研究了在Wang’s计算准则下，效用函数期望达到最大时的最优问题。以往大量的文献仅仅考虑了原保险人的利益，而在再保险过程中，往往需要考虑再保险双方的利益，因此，将原保险人和再保险人相结合进行研究亦颇具意义。曹云松[6]以原保险人和再保险人风险波动的凸组合作为目标函数，研究最优再保险的具体形式。在这些研究工作中，风险和效用函数常常作为衡量再保险合同优劣的标准。

原保险人与再保险人均希望获得更多的保费，并承担较低的风险，最优再保险策略应兼顾这两方面的关系，更直观的方法是以联合生存函数作为优化准则，寻求联合生存概率最大的再保险安排。本文主要研究在给定的时间段内，原保险人和再保险人的联合生存概率问题，即双方的理赔额均不超过各自收取的保费和初始余额之和的概率。假设发生总额为S的理赔时，原保险人承担SI,再保险人承担剩余部分SR=S-SI。我们将分别讨论成数再保险（SR=（1-a）S）和停止损失再保险(SR=(S-M)+)。本文选择期望值保费计算原理，即总保费P=(1+θ1)E(S)，再保险公司获得保费 PR=(1+θR)E(SR), 而原保险人保留剩余部分P1=P-PR，其中θ1θR为附加因子，通常θ1≤θR。原保险人和再保险人的初始余额则分别为U1、UR,则双方联合生存概率为{Pr(SI≤PI+UI,SR≤PR+UR)},我们将重点研究在给定条件下，使得联合生存概率最大的再保险策略，即

本文将通过推导和数值求解，分别给出成数再保险（比例）和停止损失再保险（非比例）的最优自留额。相对而言，成数再保险的最优解比较简单且直观，而停止损失再保险的结果则需要更多的推导。并通过具体的例子，计算停止损失再保险的最优自留额以及最大生存概率。

1 最优成数再保险

成数再保险是一种最简单的分保方式，是指原保险人与再保险人在合同中约定保险金额的分割比例，将每一风险单位的保险金额，按照约定的比例在分出公司与分入公司之间进行分割的再保险方式。成数再保险的最大特征是“按比率”的再保险，即原保险人和再保险人保险金额的分摊、保险费的分摊、赔款的分摊都是按照合同规定的同一比例来进行的。

若理赔总额为S,那么原保险人承担S1=aS,再保险人承担SR=(1-a)S,其中0≤a≤1。双方获得的保费收入分别为：

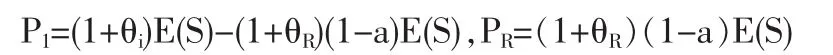
由于成数再保险的保费分摊也是按照一定比例进行的，因此θ1=θR,而为了从理论上探讨最优再保险问题，并与全文内容保持一致，我们仍将θ1、θR看成两个不同的参数，定理1给出了成数再保险的最优分保比例。

定理1 在成数再保险中，若原保险人和再保险人的初始余额则分别为U1、UR,保费计算均遵循期望值原理，则原保险人在准则(1)下的最优自留比例为

证明：在成数再保险中，赔款的分摊是按照合同规定的比例来进行的，故

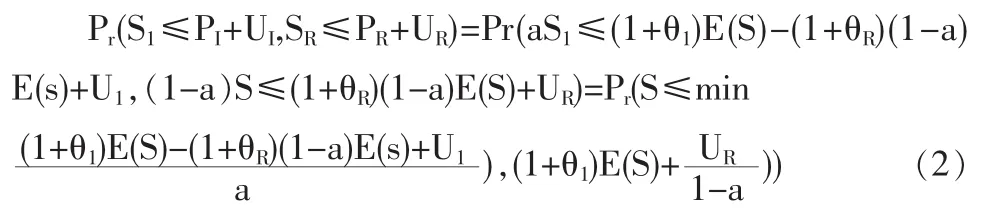
由于保险公司初始余额、附加因子以及理赔额的期望均已给定，因此联合生存概率(2)是一个关于a的函数，不妨设为G(a)，下面我们分情况讨论：

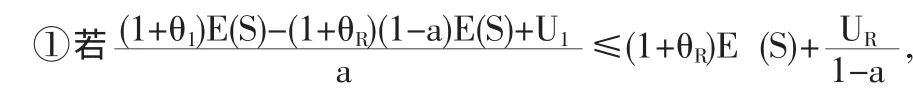
综上所述，对于成数再保险而言，由于 θI=θR，故(2)式在a=UI/UI+UR处取得最大值，从而得到了原保险人的最优自留比例。

特别的，若UR=0,则a*=1,即完全不分保时，联合生存概率最大。这个结果是显而易见的，此时联合生存函数

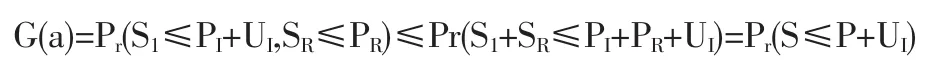
故不分保时达到最优。当然这是一种很特殊的情形，如果再保险人没有初始余额，那么在分保后双方的联合生存概率总小于不分保时原保险人的生存概率。

成数再保险是一种最基本的再保险形式，手续简单，且成本较低，双方均按约定的比例分担风险。若该比率与保险公司初始余额的比率保持一致，则联合生存概率可达到最大值。如原保险人的初始余额较高，则应自留更高比例的风险；如再保险人的初始余额较高，则可分出更多的风险。

2 最优停止损失再保险

停止损失再保险是以损失为基础来确定再保险当事人双方的责任，自留额以内的损失完全由原保险人承担，而再保险人对超过部分责任负责，即SR=(S-M)+。若损失金额（索赔额）x的密度函数为f(x)，其他条件不变，则再保险人获得保费

若给定理赔额的分布，则原保险人和再保险人的联合生存概率为M的函数G(M)，定理2给出了停止损失再保险的最优自留额及其存在的必要条件，符号和假定与前文均保持一致。

定理2 在停止损失再保险中，原保险人在准则(1)下的最优自留额M*需同时满足如下条件：

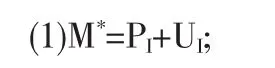
(2)损失金额S的分布函数在M*处的值F(M*

(3)联合分布函数在M*处的值不小于不分保时原保险人的生存概率，即G(M*)≥Pr(S≤P+UI).

证明：原保险人和再保险人的联合生存概率为M的函数，由停止损失再保险的性质，有：

G(M)=Pr(S1≤PI+UI,SR≤PR+UR)=Pr(S1≤PI+UI,SR≤PR+UR,SM)+Pr(SI≤PI+UI,SR≤PR+UR,S＞M)=Pr(SPI+UI,S≤M)+Pr(M≤PI+UI,S-M≤PR+UR,S＞M)

其中，UI、UR为正常数，PI、PR是关于 M 的函数， 对 PR求导可得：

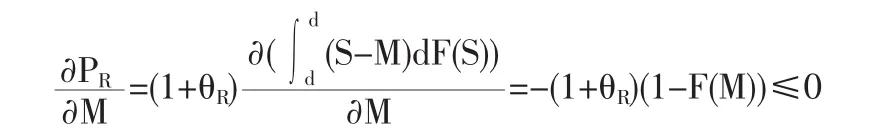
下面，我们分两种情况讨论：

①若M≥M*，则M≤PI+UI,

G(M)=Pr(S≤M)+Pr(M＜S≤PR+UR+M)=Pr(S≤PR+UR+M)

我们对函数G(M)求导：

其中f、F分别是损失分布的密度函数和分布函数，F(M)==0，并设该点为。函数G(M)在左侧递减，在右侧递增。若M*≤，则G(M)在M=0处取得最大值，而这意味着全部风险分出，这是不合理的，最优自留额不存在。因此，最优解存在的一个必要条件是M*＞，即损失金额S的分布函数在M*处的值

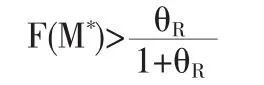
则函数G(M)在M*处取得最大值。

②若 M＞M*，则 M＞PI+UI,G(M)=Pr(S≤PI+UI),在此情形下，

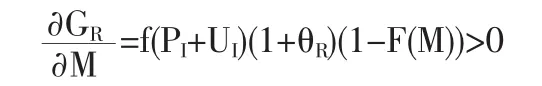
综上所述，停止损失再保险的最优自留额须满足定理条件(1)、(2)，并且最优联合生存概率不应小于不分保时原保险人的生存概率。

需要特别注意的是，函数G(M)在M*处是不连续的。左极限

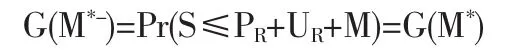
而右极限

显然G(M*-)＞G(M*+)。事实上，在情形①中，风险自留额不超过原保险人保费与初始余额之和，我们只需考虑再保险人的生存概率；情形②中，风险自留额大于原保险人保费与初始余额之和，所以必须保证原保险人损失额小于保费与初始余额之和，而此时再保险人不需要理赔，必然生存。由于我们考虑的是双方同时生存的概率，停止损失再保险合同又可以看成是一类分段函数，从而导致联合生存概率函数在M*处不连续的。下面，我们通过两个实际的例子，计算停止损失再保险的最优自留额。

3 实例分析

指数分布：若理赔额S服从期望为100的指数分布，即f(S=x)，μ=100。若停止损失再保险的自留额为M，则再保险人获得保费

其中，附加因子θ1=0.1,θR=0.2，双方的初始余额分别为UI=40，UR=10。 运用数值方法，可获得方程 （1+θI）μ-(1+θR）μe=M 的根 M*≈110.1,此时显然 。 联合生存概率G(M*)=0.7980。如不分保，原保险人的生存概率为

F(S≤P+UI)=0.7769＜G(M*)

因此，M*≈110.1即为停止损失再保险在联合生存概率准则下的最优自留额。

帕累托分布：若理赔额S服从期望为100的帕累托分布，即 f(S=x)，其中 k=400,α=5,其他条件同上，则再保险人获得保费

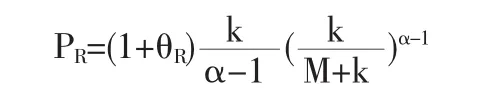
原保险人保留保费

F(S≤P+UI)=0.7956＜G(M*)

因此，M*≈110.4为帕累托分布下停止损失再保险的最优自留额。

4 小结

本文以原保险人和再保险人的联合生存概率最大化为准则，分别探讨了两类常见的再保险形式：成数再保险和停止损失再保险的最优策略。研究结果表明，成数再保险的最优策略与双方的初始余额直接相关。而停止损失再保险的最优策略须使得自留额与原保险人剩余保费相等，同时满足最优解存在的必要条件。此外还通过具体实例验证结论。基于该准则的最优再保险策略兼顾了再保险当事人双方的利益，可为保险公司与再保险公司的决策提供有力依据。

[1]Pesonen,M.L.Optimal Reinsurances[J].Scandinavian Actuarial Journal,1984,84.

[2]Gajek,L.,Zagrodny,D.Insurer’s Optimal Reinsurance Strategies[J].Insurance:Mathematics and Economics,2000,27.

[3]Kaluszka,M.Optimal Reinsurance Under Mean 2 Variance Premium Principles[J].Insurance:Mathematics and Economics,2001,28.

[4]Young,V.R.Optimal Insurance under Wang’s Premium Principle[J].Insurance:Mathematics and Economics,1999,25.

[5]Young,V.R.Discussion of Christofides’Conjecture Regarding Wang’s Premium Principle[J].ASTIN Bulletin,1999,29(2).

[6]曹云松.最优再保险的研究[D].浙江大学硕士论文，2006.