极大似然估计的间接求法
2010-05-18顾蓓青王蓉华徐晓岭吴生荣
顾蓓青,王蓉华,徐晓岭,吴生荣
(1.上海对外贸易学院 商务信息学院,上海 201620;2.上海师范大学 数理学院,上海 200234;3.宜兴出入境检验检疫局,江苏 宜兴 214200)
1 全样本极大似然估计
设连续型总体X的分布函数和密度函数分别记为FX(x,θ)和 fx(x,θ),x∈(a,b),-∞≤a<b≤∞,θ 为未知参数。 而 X1,X2,…,Xn为来自总体X的容量为n的一个简单随机样本,x1,x2,…,xn为其观察值。
记(X1,X2,…,Xn)的联合密度也即似然函数为 Lx(θ),则
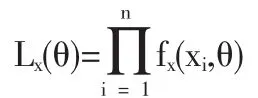
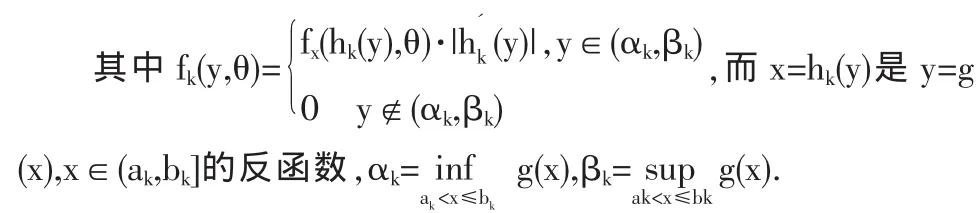
令函数y=g(x),a<x<b其不含有任何未知参数。如果可以把(a,b)分为(有穷个或可列个)两两不交的区间(ak,bk],k=1,2…,使y=g(x)在每一个小区间上满足严格单调且反函数连续可微,则随机变量Y=g(X)的密度函数为:
fY(y,θ)Σk
fk(y,θ),y∈(-∞,∞)
令 Yi=g(Xi),i=1,2,…,n,则 Y1,Y2,…,Yn为来自总体 Y 的容量为n的一个简单随机样本,y1,y2,…,yn为其观察值。
记(Y1,Y2,…,Yn)的联合密度也即似然函数为 LY(θ),则
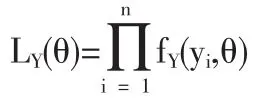
注意到,对 xi,i=1,2,…,n 总存在 ki,使 xi∈(aki,bki],也即对yi∈(αki,βki],有
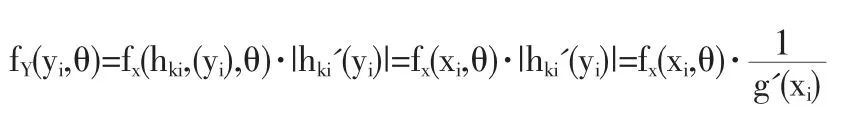
于是 LY(θ)=易知
即用总体X的样本X1,X2,…,Xn得到的参数θ的极大似然估计与用总体Y的样本Y1,Y2,…,Yn得到的参数θ的极大似然估计是相同的。
例 1:设总体 X 服从对数正态分布,记为 X~LN(μ,σ2),其密度函数为:fX(x,μ,σ2)=其中 μ,σ2是未知参数,X1,X2,…,Xn是 X 的一个样本,求 μ,σ2的极大似然估计。
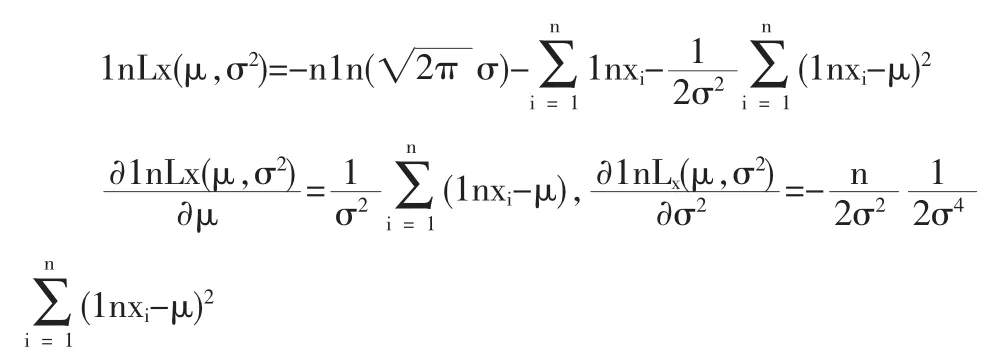
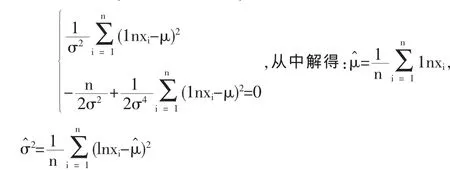
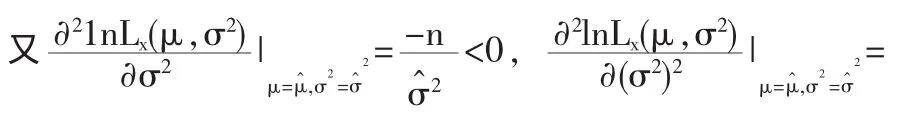
则μ,σ2的 MLE 为:
解法二:若 X~LN(μ,σ2),则 Y=lnX~N(μ,σ2).令 Yi=lnXi,i=1,2,…,n由此Y1,Y2,…,Yn为来自正态分布总体Y一个简单随机样本,易知参数 μ,σ2的 MLE 为
例 2:设总体 X 服从 U[-θ,θ],θ>0 为未知参数,其密度函数为 fx(x,θ)=
,X1,X2,…,Xn是 X 的一个样本,X(1)≤X(2)≤…≤X(n)为其次序统计量。求θ的极大似然估计。解法一:似然函数为:
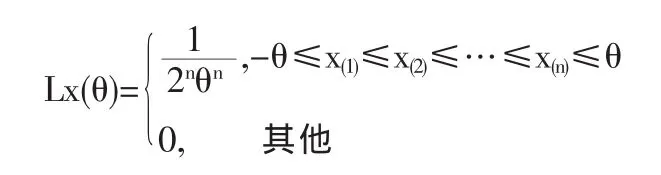
则从总体X出发得到参数θ的极大似然估计为:
θ^=max(|X1|,|X2|,…,|Xn|)=max(|X(1)|,|X(n)|)
解法二:令函数 y=x2,-θ≤x≤θ,此函数分为两段,即在[-θ,0)段上它严格单调下降,反函数连续可微,而在段上严格单调上升,反函数连续可微。
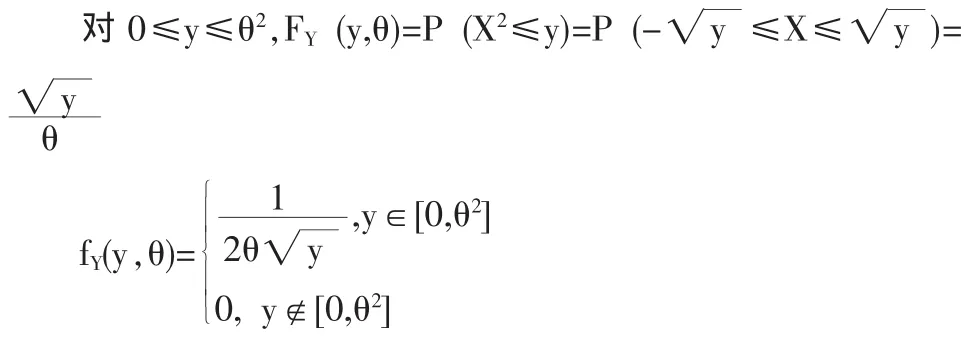

2 定数截尾样本(单增)极大似然估计
设连续型总体X的分布函数和密度函数分别记为FX(x,θ)和 fx(x,θ),x∈(a,b),-∞≤a<b≤∞,θ 为未知参数。 而 X(1)≤X(2)≤…≤X(r)为来自总体X的容量为n的前r个次序统计量,x(1)≤x(2)≤…≤x(r)为其观察值。
记(X(1)≤X(2)≤…≤X(r))的联合密度也即似然函数为 LX(θ),则
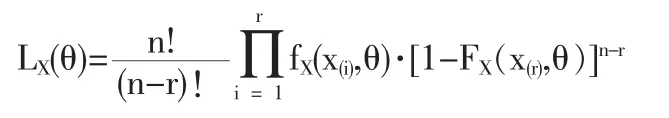
令函数y=g(x),a<x<b其不含有任何未知参数,并对x是严格单调增加的。 记其反函数为 x=h(y),g(a)<y<g(b)。
令 Y=g(X),Y(i)=g(X(i)),i=1,2,…,r 则 Y(1)≤Y(2)≤…≤Y(r)为来自总体Y的容量为n的前r个次序统计量,y(1)≤y(2)≤…≤y(r)为其观察值。 对 y∈(g(a),g(b)),记(Y(1)≤Y(2)≤…≤Y(r))的联合密度也即似然函数为 LY(y,θ),则
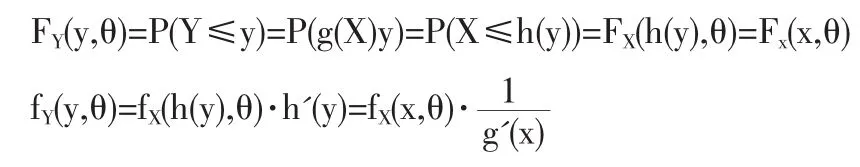
即用总体 X 的前 r个次序统计量 X(1)≤X(2)≤…≤X(r)得到的参数θ的极大似然估计与用总体Y的前r个次序统计量,Y(1)≤Y(2)≤…≤Y(r)得到的参数θ的极大似然估计是相同的。
3 定数截尾样本(单减)极大似然估计
设连续型总体X的分布函数和密度函数分别记为FX(x,θ)和 fX(x,θ),x∈(a,b),-∞≤a<b≤∞,θ 为未知参数。 而 X(1)≤X(2)≤…≤X(r)为来自总体X的容量为n的前r个次序统计量,x(1)≤x(2)≤…≤x(r)为其观察值。
记(X(1)≤X(2)≤…≤X(r))的联合密度也即似然函数为 LX(θ),则
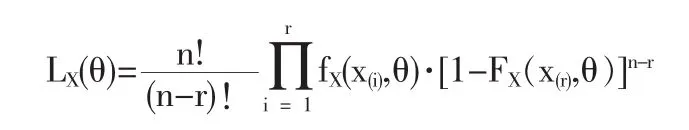
令函数y=g(x),a<x<b其不含有任何未知参数,并对x是严格单调递减的。记其反函数为x=h(y),g(b)<y<g(a).
令 Y=g(X),Y(i)=g(X(n-i+1)),i=n-r+1,n-r+2,则 Y(n-r+1)≤Y(n-r+1)≤…≤Y(n)为来自总体Y的容量为n的后r个次序统计量,Y(n-r+1)≤Y(n-r+2)≤…≤Y(n)为其观察值。 对 y∈(g(b),g(a)),
FY(y,θ)=P(Y≤y)=P(g(X)≤y)=P(X≥h(y))=1-FX(h(y),θ)=1-FX(x,θ)
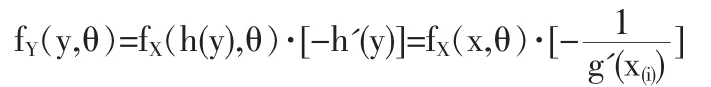
记Y(n-r+1)≤Y(n-r+2)≤…≤Y(n)的联合密度也即似然函数为LY(θ),则
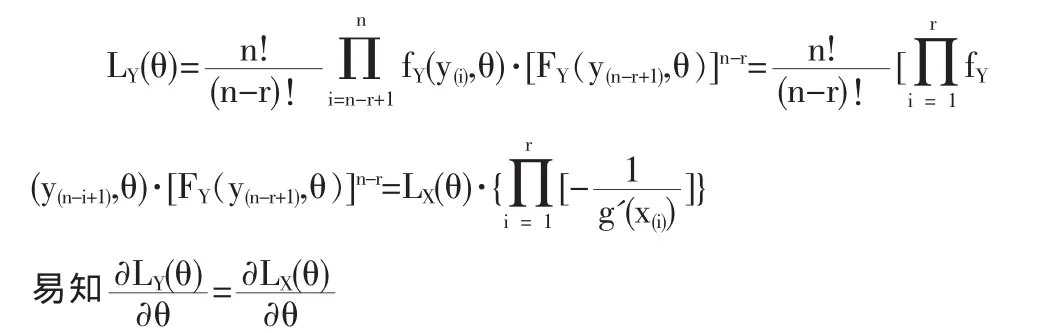
即用总体 X 的前 r个次序统计量 X(1)≤X(2)≤…≤X(r)得到的参数θ的极大似然估计与用总体Y的后r个次序统计量Y(n-r+1)≤Y(n-r+2)≤…≤Y(n)得到的参数θ的极大似然估计是相同的。
例 3:设总体 X服从 U[0,θ],θ>0为未知参数,其密度函数为fx(x,θ)=是 X 的容量为 n 前 r个次序统计量。求θ的极大似然估计。

解法二:令函数 y=ex,x∈[0,θ],此为严格单调增函数。 令Y=eX,Y(i)=eX(i),i=1,2,…,r,则 Y(1),Y(2),…,Y(r)是 Y 的容量为 n前r个次序统计量。
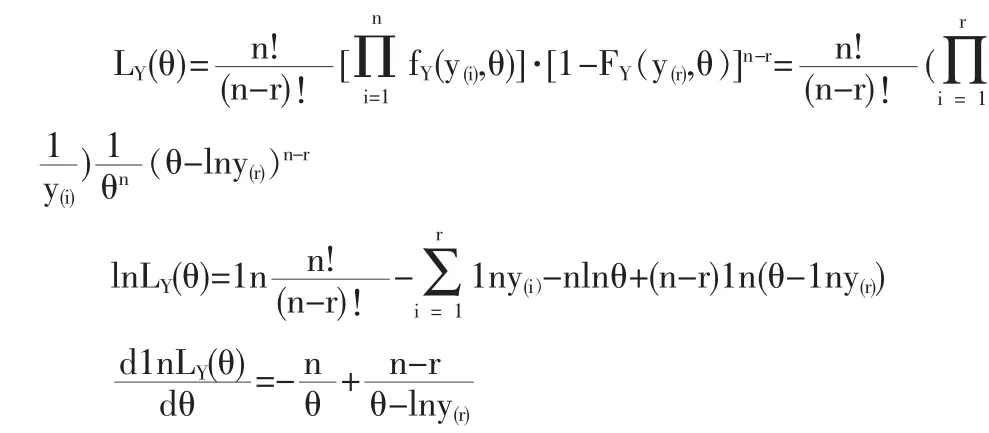
解法三:令函数 y=e-x,x∈[0,θ]此为严格单调减函数。 令Y=e-X,Y(i)=e-X(n-i+1),i=n-r+1,n-r+2,…,n,则 Y(n-r+1)≤Y(n-r+2)≤…≤Y(n)是Y的容量为n后r个次序统计量。对e-θ≤y≤1,
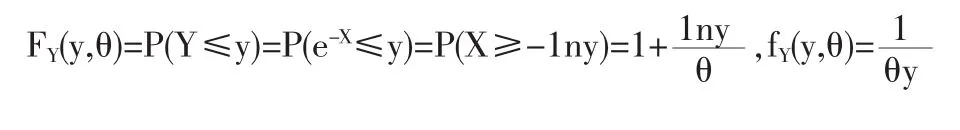
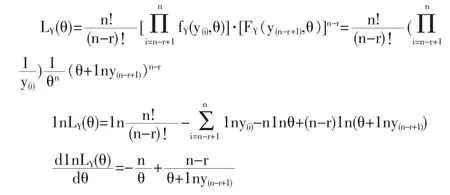
4 一般情况
设总体 X 的分布函数和密度函数分别为 F(x,θ),f(x,θ),X1,X2,…,Xn为X的容量为n的一个简单随机样本,如果仅知道 X(n1),X(n2),…,X(ns)(1≤n1<n2<…<ns≤n)这 s个观察值。 而这 s个次序统计量 X(n1),X(n2),…,X(ns)(1≤n1<n2<…<ns≤n)的联合密度函数也即似然函数为:
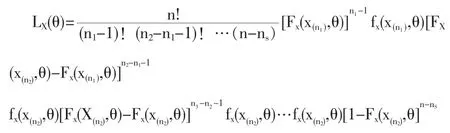
利用上述似然函数可得参数θ的极大似然估计θ^1。
令函数 y=g(x),其为严格单调函数,令 Y=g(X),Y(ni)=g(X(n2)),i=1,2,…,s则可利用来自总体Y的s个统计量Y(ni)=g(X(ni)),i=1,2,…,s的联合密度可求得参数θ的极大似然估计θ^2,而且有θ^1=θ^2。
[1]孙祝岭,徐晓岭.数理统计[M].北京:高等教育出版社,2009.
[2]叶中行,王蓉华,徐晓岭,白云芬.概率论与数理统计[M].北京:北京大学出版社,2009.
[3]汪荣鑫.数理统计[M].西安:西安交通大学出版社,1986.
[4]周概容.概率论与数理统计[M].北京:中国商业出版社,2006.
[5]茆诗松,周纪芗.概率论与数理统计[M].北京:中国统计出版社,2000.
