基于支持向量机的上市公司信用风险评估研究
2010-05-18唐建荣谭春晖
唐建荣,谭春晖
(江南大学 商学院,江苏 无锡 214122)
0 引言
信用风险又称为违约风险,是指借款人、证券发行人或交易对方因种种原因不愿或不履行合同条件而构成违约,致使银行、投资者或交易另一方遭受损失的可能性[1]。国内外不少学者对信用风险评估问题进行了探索和研究,但由于缺乏足够的数据,传统的分析方法显得捉襟见肘。本文引入一种基于小样本学习的方法——支持向量机(SVM),并运用其构建商业银行信用风险模型,取得了较好的评估效果[2]。
支持向量机(SVM)是在高位特征空间使用线性函数假设空间的学习系统,它由一个来自最优化理论的学习算法训练。此学习策略由Vapnik和他的合作者提出,是一个准则性的并且强有力的方法[3]。
1 信用风险评估实证分析
支持向量机对企业预期违约概率的度量主要有以下四个步骤:(1)样本空间的选择。一般来说,以企业资产价值作为标准来选择违约企业,并注重这些企业资产价值的均值、标准差和范畴。(2)选取解释变量。在企业违约风险度量分析中,作为解释变量的财务指标的设计和选取关系到支持向量机和预测企业信用状况的成败。上市公司的信用数据主要来源于企业不同时期的财务报表,如资产负债表、损益表和现金流量表等,以及企业资产、债务等的市场价值或价格。(3)模型分析。运用支持向量机分析选取最优的财务指标,将其转换为唯一的企业信用状况判别值,并在此基础上度量企业的预期违约概率。(4)模型检验。利用不同的统计量对模型结果进行验证,对模型是否准确预测企业违约做出评价[3]。
1.1 样本描述
经营失败企业的财务数据难以搜集,在很大程度上阻碍了企业违约风险的理论和实证研究。中国证监会要求上海证券交易所和深圳证券交易所对企业经营出现异常状况的上市公司的股票实行特别处理,这些上市公司的财务数据可以替代度量企业的信用违约风险。
本文选取沪深两市的150多家上市公司的财务比率数据进行分析,数据来源于金融界网站。其中样本由经营正常组和经营失败组组成,排除掉一些数据缺失的企业,最终留下123家有效企业数据,其中包括经营正常组73家,经营失败组50家,见表1。
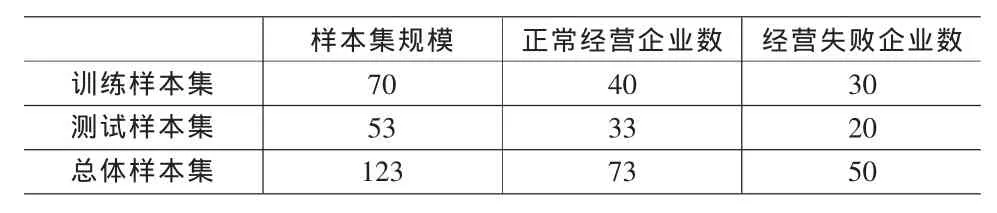
表1 样本分布情况
行业的划分是按照中国证券监督管理委员会关于上市公司行业划分的最新方法,样本来自包括农业、各类制造业、房地产业、商业和零售业、其他各种服务业和综合业。
1.2 解释变量的选择
论文考虑了各方面的影响要素,依据指标选取原则,参照常用的企业绩效评价指标体系和国内外文献的相关研究,从金融机网站中选取了反映上市公司财务状况的偿债能力、每股收益、经营效率、盈利能力和财务结果等6方面的财务比率数据[8]进行分析(见表2)。对这16个财务比率指标进行主成分分析,最终得到10个主成分,使其尽可能多的包含原始数据的大部分信息并解决了指标变量之间的多重共线性问题。
1.3 模型实证分析
设模型样本数为 n,X=(X1,X2,…,Xp)T是一个 P 为向量,X是模型选取的财务比率指标矩阵。构造样本集(x,y),x维数为10,y是样本的类别,设经营正常企业y=1,经营失败企业y=-1。支持向量机中有多种不同的核函数,主要包括径向基核函数,稳态高斯核函数,多项式核函数,双曲正切核函数等。有研究表明,不同的核函数得到的结果性能相差不大[7]。本文构造的支持向量分类模型的核函数采用最常见的径向基核函数:K (xi,xj)=e-|xi-xj|/2σ2。本文使用OSU SVM Classifier Matlab Toolbox3.0工具包进行分析。
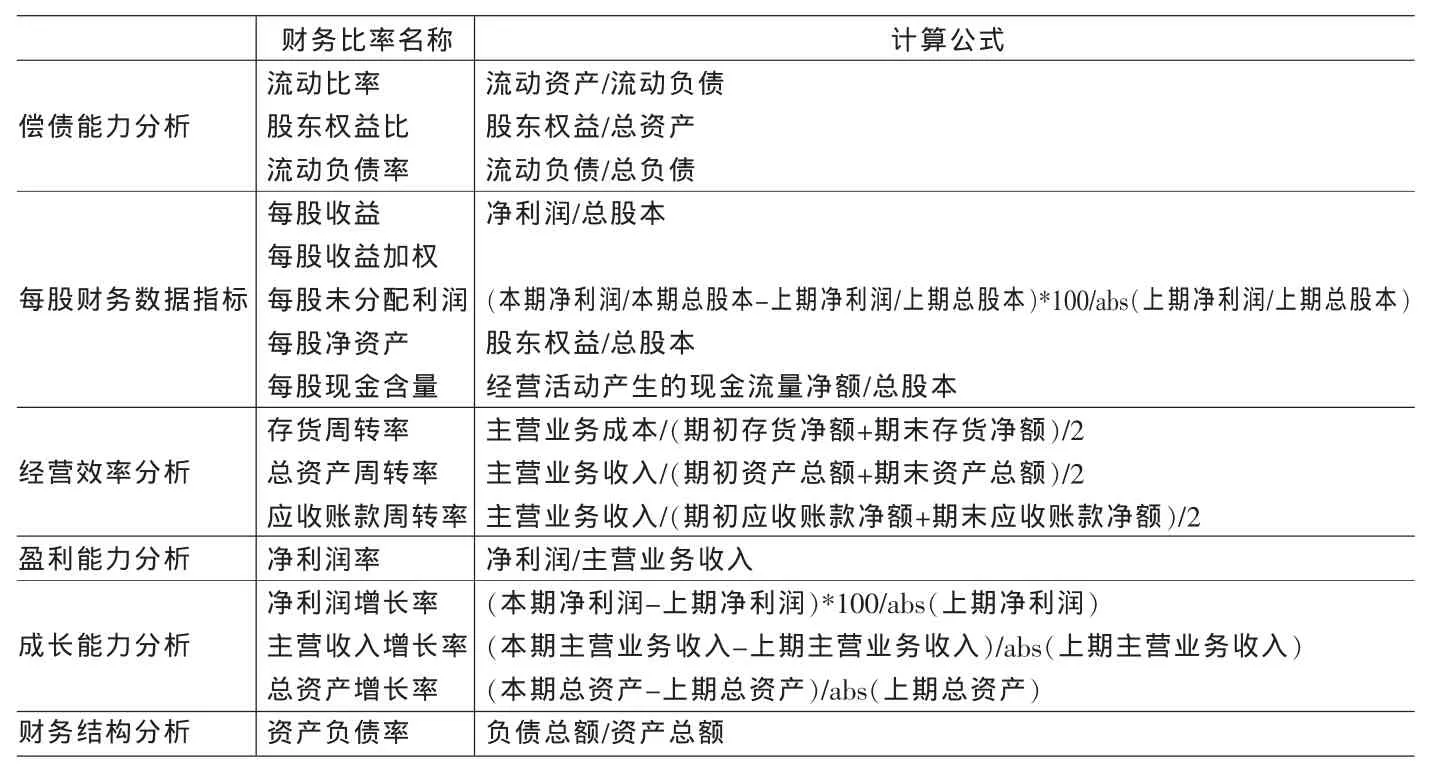
表2 模型使用的财务比率指标
不同的径向基核函数的参数惩罚系数C和σ2取值不同,所得到的支持向量个数、第一类错误误识率,第二类错误误识率、准确率也不尽相同。通过反复试算选取最佳的核函数参数:
当σ=1时,无论惩罚因子C取何值,通过Matlab软件得到的模型的支持向量的个数为69,对测试样本进行预测:第一类错误,即将违约企业错分为正常企业的概率为25%,第二类错误:即将正常企业错分为违约企业的概率都为24.24%,测试样本的准确率为75.47%。由此可知,当σ=1时,模型对惩罚因子C的变化并不敏感;
当σ=5时,随着惩罚系数C的不断变化,模型所得到的支持向量的个数不断变化。当C=1时所得到的支持向量的个数为49,随着C的不断增加,支持向量的个数不断减少。当C=50时,模型所得支持向量个数减少至23,接着又随C的增加而增加。第一类错误误识率在15~20%,第二类错误误识率随着C的不断增加而增加,C=1时达到最小,为9.09%,测试样本的准确率也随着C的不断增加而减少,C=1准确率达到86.79%;
当σ=10时,支持向量的个数随C的不断增加而减少,当C=800时支持向量个数为24,此时达到最少。第一类错误误识率在10~20%之间,第二类错误误识率随C的不断增加而不断提高,测试结果的准确率随C的不断增加而降低,当C=10和C=30时,准确率最高,为86.79%。
第一类错误为将违约企业错分为正常企业,第二类错误为将正常企业错分为违约企业,两类错误相比较,第一类错误较为严重,第二类错误的发生,仅仅是失去可以偿还贷款的客户,损失的只是贷款所得的利息;而第一类错误的发生,将直接导致银行严重的损失,银行放贷给违约企业,损失的是本金和利息。因此要严格控制第一类错误的发生。部分模拟结果(见表 3)显示:δ=5,C=1;δ=10,C=10;δ=10,C=30 三组核函数参数所得到的准确率相等,都为86.79%,但是第一类错误误识率,第二类错误误识率都不相同。综合考虑,本文最终选择σ=10,C=30的模型,此时第一类错误误识率为15%,第二类错误误识率为12.12%,准确率为86.79%。
1.4 比较分析——多元判别分析MDA
本文在实证分析中采用逐步判别分析,并借助SPSS16.0软件实现。
1.4.1 多元判别分析建模
假设模型样本企业数为n,X=(X1,X2, …,Xp)T是一个 p 维向量,X是模型选取的企业财务比率,i为财务比率的数量,bi是判别系数,b0是常数项。令Zu为企业u的经营状况判别值,判别方程为:
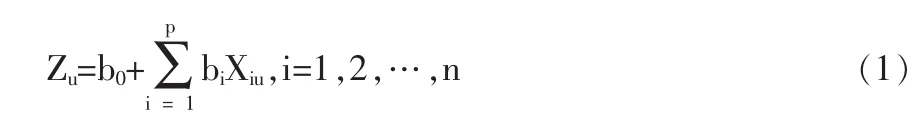
线性判别分析采用线性判别法则来分类和预测企业经营失败与否。将企业u划入经营失败组g的原则是u属于组g的后验概率大于其属于经营正常组g’的后验概率,即:

为与支持向量分类机模拟出来的结果对比,样本选取和指标的选取都与支持向量机的样本一致。本文采用SPSS16.0对样本进行多元判别分析。
1.4.2 结果分析
通过SPSS逐步判别分析逐步进入判别方程式的变量为主因子A1,主因子A8和主因子A7。模型采用系统默认的分析方法和判据:进入模型的F值为3.84,从模型中剔除变量的F值为2.71。通过判别分析得到判别函数Z=0.714A1+0.399A7-0.487A8+0.048,非标准化判别函数系数,即费歇尔判别函数系数。预测变量的原始数据乘以判别系数得到判别得分。两组在判别函数上的重心不同(-1.179,0.885)。根据组重心函数值可以得到 Z0临界值0.147,当Z得分大于-0.147时为组1不违约组,当Z得分小于-0.147时为组-1即违约组。
应用所得到的模型做判别预测。本文所使用的测试组样本与支持向量机的测试组样本一致。使用判别方程式计算测试样本的判别得分,并且根据所得的临界值-0.147进行判别预测。
1.5 结果分析
多元判别分析的判别预测结果,从表3中可知,对训练样本的回测准确率为91.43%,其中第一类错误,即将违约企业的概率判定成正常企业的概率为20%;第二类错误,即将正常企业判定成违约企业的概率为0;对预测样本进行预测的结果为准确率为84.91%,其中第一类错误率为25%,第二类错误率为9.09%。
表3中仅列出支持向量分类机核函数参数σ取不同值时所得的最优判别结果。
支持向量分类机对训练样本重新进行回测,准确率为100%。从预测结果中选择最优的预测结果,即σ=10,C=30测试样本分类的准确率为86.79%,第一类错误15%,第二类错误12.12%。通过比较可知,支持向量机无论是训练样本的回测还是对未知类别测试样本的预测准确率高于多元判别分析,而两类错误发生的概率也都低于多元判别分析。
2 结束语
支持向量机能够较好的解决小样本、高维数和局部极小点等实际问题。本文构建了一种基于支持向量机的上市公司信用风险评估模型,通过与多元判别分析的比较,发现支持向量机具有比较高的准确率和较低的第一类错误率。
研究中也遇到一些未能解决的问题,本文只解决了支持向量机的两类分类问题。实际上应当推广到更为复杂的多类信用等级评估研究以更精确的反映上市公司的信用情况,为银行、投资者提供更有利的辅助工具。论文模型中第二类错误率控制的较好,但是引起较大损失的第一类错误率较高,本文中第一类错误和第二类错误的惩罚因子选取相同,如有可能应当选取不同的惩罚因子。在惩罚因子C和核函数参数的选择上还没有成熟的理论支持和方法,只能通过不同惩罚因子C和核函数参数的不断试算结果中,选取结果最好的一组参数构造模型并且进行企业违约与否的预测。
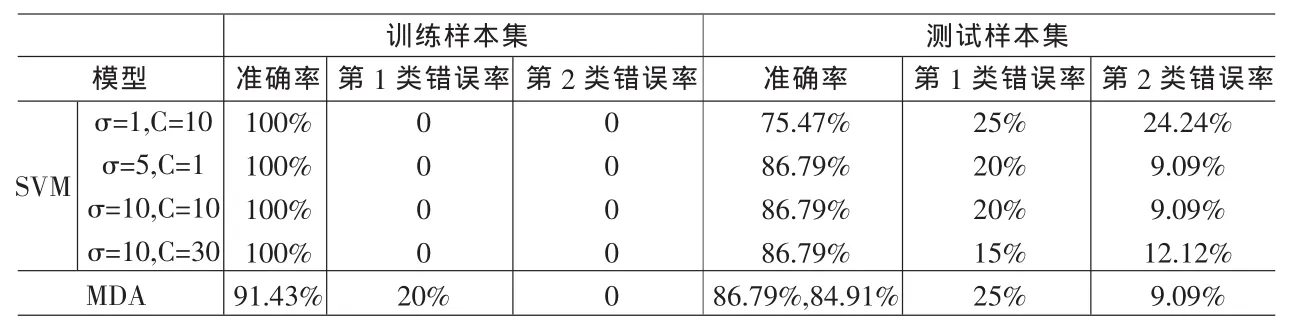
表3 模型判别结果
[1]邹新月,李汉通.运用典型多元判别分析法评估上市公司信用风险[J].统计与决策,2007,(7).
[2]美Cristianini,N.著,李国正等译.支持向量机导论[M].北京:电子工业出版社,2004.
[3]梁琪.商业银行信贷风险度量研究[M].北京:中国金融出版社,2005.
[4]Cortes C’Vapnik V.Support-vector Networks[J].Machine Learning,1995,20(3).
[5]Vapnik V N著,张学工译.统计学习理论的本质[M].北京:清华大学出版社,1990.
[6]张树德.MATLAB金融计算与金融数据处理[M].北京:北京航空航天大学出版社,2008.
[7]侯惠芳,刘素华.基于支持向量机的商业银行信用风险评估[J].计算机工程与应用,2004,(31).
[8]原始财务比率数据略(来源于金融界网站http://stock.jrj.com.cn/cominfo/AllStock.asp)
