基于三维重建技术的三角剖分*

谷利国，侯振杰

（内蒙古农业大学 计算机与信息工程学院,内蒙古 呼和浩特010018）

在计算机视觉中,三维重建是指由多幅二维图像恢复物体三维可见表面几何形状的方法（物体的空间位置信息）。三维重建直接模拟人类双眼处理景物的方式，具有简单、可靠、灵活、使用范围广等特点，可以进行非接触、自动、在线检测等。

从某种角度上说，三维重建的最终目的是可视，就是把被重建的物体真实地显示出来。由三维重建算法得到的是一组三维点集，并不能求得整个物体表面的细节，因此需要对这些散乱的三维点进行三角剖分，用许多小三角形组成的表面来近似物体表面，这样就相当于给散乱的三维点集搭起一个立体的网状骨架模型。经过三角剖分之后，所有三角形的平面片在空间撑出了物体的三维模型。这时只需要将物体的纹理从图像中取出，并映射至三维模型上就可以提供物体的真实三维模型。

三角剖分是虚拟现实、计算机视觉等领域的一个研究热点。目前针对三角化的研究主要有：BOLL和VEMURI[1]、BRINKLEY和 SCHMITT等采用参数表示法，将三维数据映射到二维参数域上,在二维进行曲面重构,然后将结果映射回三维空间；BOWYER和 WATSON[2]采用Delaunay三角剖分法,将二维的Delaunay三角剖分推广到三维进行网络重构。BERNARIDINI的 BPA算法[3]通过种子三角形不断向周围扩展，从而构成最终的三角形网格等。

目前,对于平面区域的散乱点集三角剖分已经取得了一定的成果，但很多算法推广至三维空间仍存在一些问题，在算法的时间效率上也有待进一步提高，因此对于三维空间散乱点集的三角剖分有待进一步的发展。

本文提出了一种利用增量法与分治法相结合的算法，直接对空间散乱点进行三角剖分，降低算法的时间复杂度，并通过编程证明了该算法的可行性。

1 三角剖分算法的基础理论

三角剖分中以Delaunay三角剖分最具有代表性，它是优化的三角剖分。Delaunay三角剖分的概念是1934年由俄国数学家Delaunay提出的。

三角剖分所具备的优异特性主要有以下几个方面：

(1)最接近：以最临近的三点形成三角形，且各线段(三角形的边)皆不相交；

(2)唯一性：不论从区域何处开始构建，最终都将得到一致的结果；

(3)最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形6个内角中最小的角度不会变大；

(4)最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大；

(5)区域性：新增、删除、移动某一个顶点时只会影响临近的三角形；

(6)具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

关于Delaunay三角剖分主要有三类:增量算法(逐点插入法)、分治法(分割归并算法)和三角网生长算法。三角网生长法在20世纪80年代中期以后就很少用到,较常见的是分治算法和逐点插入法。

增量算法的思想：先构造一个包含所有点集的大三角形，然后逐点在三角形内插入点，插入的过程不断用Delaunay三角优化准则去检查和调整，直到所有点插入完整，算法结束。

逐点插入法有不同的实现方法，区别在于初始多边形的不同和初始三角剖分的方法不同。较有代表性的是Lawson算法[4]以及 Lee和 Schacher算法[5]。

分治算法的思想：所谓的分治法，其实就是分而治之。首先把要处理的点集分成几个相等的子点集，按Delaunay三角优化准则对各子点集进行三角剖分，然后把各个子集的相邻三角形边界进行合并，最后对合并时在子集边界处新生成的三角形进行优化。

分治法也有不同的实现方法,其不同之处在于使用不同的子集划分方法、子集中三角剖分方法或者各子集边界的合并方法，比较经典的算法是Lee和Schacher算法[5]、Dwyer 算法[6]。

2 改进的三角剖分算法

2.1 复杂度及优缺点分析

增量算法简单直观，占用内存小，鲁棒性好，容易实现，但时间复杂度差,最坏情况为O(n2)。当处理的散乱点数量增长时，处理的时间也指数地增长，故降低其时间复杂度显得相当重要。

分治算法时间复杂度方面较好，其最坏情况为O(lgn)，但由于递归执行，需要较大的内存空间，对于大规模的散乱点的处理要求大量的内存空间。

两种算法各有自己的优点和缺点，增量算法时间效率差，节省内存空间;而分治法时间效率好，但需要大量内存。

改进的算法思想是把分治算法与增量法结相结合，以分治算法为主体,增量法为辅：当递归分割数据点集的过程进行到子点集中的数据量小于一个预定值——分割阈值时终止,然后用增量法在子集中生成子三角网。这一新的算法称为合成算法。

2.2 算法的改进

2.2.1 分治法中的改进

分治法中采用一对八式的八叉树数据模型来完成分割与合并。

首先利用八叉树模型对空间离散点进行分割，然后对八叉树叶子节点进行Delaunay三角化，最后依据Delaunay法则将各局部三角网自下而上逐级合并，进而生成最终的整个点集三角网模型,这样将两种三角化适当结合，提高了算法的效率。

其中，在合并的过程中尽量减少了查找正确扩展点的范围，从而节约了时间，提高了算法的执行效率。

具体作法：将各节点生成三角网凸壳的扩展边（边界）找出，用链表分别存储，两两合并三角网时所需用到的边和点就可直接取自这两条链表中的数据，而无需在该区域中所有点中逐一比较寻找了，从而避免了很多无用功。

用八叉树来表示三维形体，既可以看成是四叉树方法在三维空间的推广，也可以认为是用三维体素阵列表示形体方法的一种改进,如图1所示。

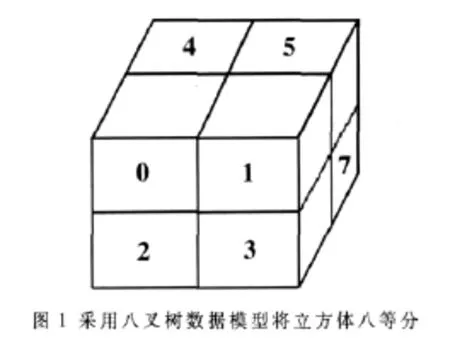
八叉树有三种不同的存储结构，分别是规则方式、线性方式以及一对八方式。相应的八叉树也分别称为规则八叉树、线性八叉树以及一对八式八叉树。不同的存储结构的空间利用率及运算操作的方便性是不同的。分析表明，一对八式八叉树优点更多一些。

(1)规则八叉树

规则八叉树缺陷较多，最大的问题是指针占用了大量的空间。假定每个指针要用2 B表示，而节点的描述用1 B,则存放指针要占总存储量的94%。因此，这种方法虽然十分自然，容易掌握，但在存储空间的使用率方面不是很理想。

(2)线性八叉树

线性八叉树不仅节省存储空间，对某些运算也较为方便,但是为此付出的代价是丧失了一定的灵活性。

(3)一对八式的八叉树

一个非叶节点有8个子节点，为了确定起见，将它们分别标记为 0、1、2、3、4、5、6、7。综上所述，如果一个记录与一个节点相对应，那么在这个记录中描述的是这个结点的8个子节点的特性值。而指针给出的则是该8个子节点所对应记录的存放处，而且还隐含地假定了这些子结点记录存放的次序。也就是说，即使某个记录是不必要的(例如该节点已是叶节点)，则相应的存储位置也必须空闲在那里，以保证不会错误地存取到其他同辈节点的记录。这样当然会有一定的浪费，除非它是完全的八叉树，即所有的叶节点均在同一层次出现，而在该层次之上的所有层中的节点均为非叶节点。

综上优缺分析后，文中选择了一对八式的八叉树数据模型。

2.2.2 Delaunay增量算法的改进

Delaunay增量算法的思想是逐点插入,每次插入一个散乱点，经处理形成若干新的四面体;但随着插入点的增加，所生成的四面体便成倍地增长，而计算量也大大增加。

如何缩短算法中各个环节的计算时间成为提高整个算法效率的关键。这些关键问题涉及散乱点的加入方式、搜索方法等。

本文在搜索四面的外接圆时使用了指南针算法，提高了算法的搜索效率。

2.3 可行性分析

(1)采用八叉树分割，并用递归的思想，当数据量大的时候，调用的程序运行效率比较低。在本程序的实现中，将递归调用转化为迭代，从而提高算法效率[7,8]。

(2)文中在增量算法中嵌入了指南针算法搜寻四面体外接球体，以加快算法的搜寻速度。

(3)在合并的过程中尽量缩小查找正确扩展点的范围,提高了算法的执行效率。

3 实验

本文的实验环境：CPU为Pentium(R)Dual-Core 2.5GHz，内存1 GB，显卡为集成显卡，操作系统为 Window XP，仿真平台为Matlab 7.0。

(1)选取通过三维扫描仪得到的点云图，分别利用Matlab中的Delaunay（）函数剖分和改进的三角剖分算法对点云图进行剖分，在点数变化时，对两种算法所剖分出四面的数量和所用时间进行比较,结果如表1所示。

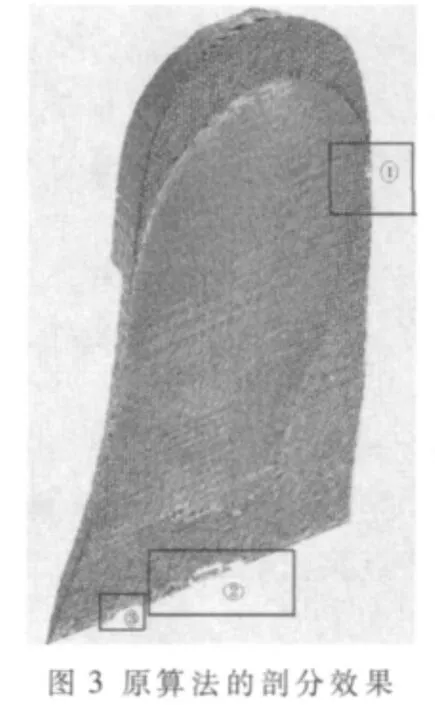
(2)选取通过三维扫描仪得到的一条围巾的点云图，分别利用 Matlab中 Delaunay()函数、Delaunayn()剖分和改进的三角剖分算法对点云图进行剖分。通过三维扫描仪扫描围巾得到点云,如图2所示，使用原算法和改进算法对围巾点云图进行三角剖分，结果如图3和图4所示。

对图3和图4中的1号与2号区域放大,比较效果分别如图 5、图 6、图 7、图 8所示。

使用两种算法对围巾点云剖分在剖分出四面的数量和所用时间方面进行比较,结果如表2所示。

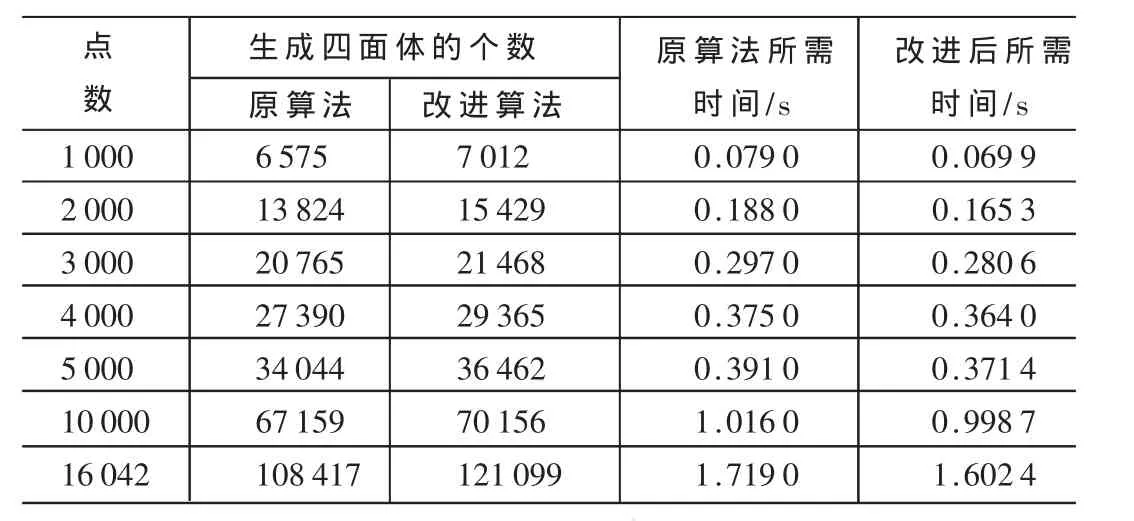
表1 对三维扫描仪得到的三维点进行三角剖分

通过对不同数量的空间散乱点的三角剖分，利用Matlab内置的Delauany()函数与改进的三角剖分算法对空间散乱点集进行三角剖分，对剖分出四面体的数量和所用时间进行比较，改进的算法在剖分出的四面体数量和时间效率上有明显的优势。而且由以上图的比较可以看出，对于重建出的模型效果，改进后的算法明显优于前者。

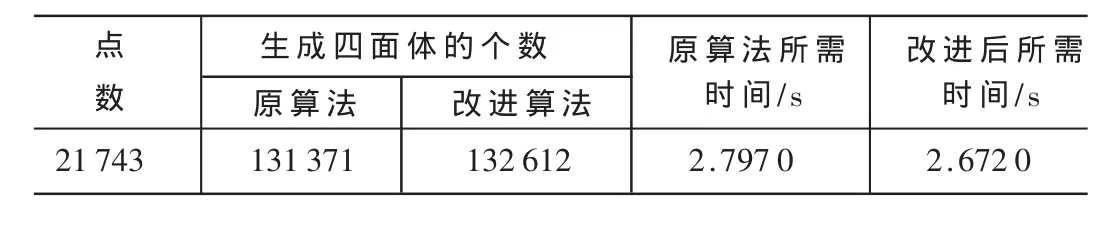
表2 算法效率分析

本文算法通过使用分治法和增量法的合成算法，在分治法中使用八叉树数据模型，使递归问题转化为迭代问题，提高了算法的执行效率；在增量法中嵌入指南针算法，提高了搜索效率。使用合成算法在空间的三角剖分方面有很大的优势。此外分析了算法中的不足之处，并提出有待进一步研究的问题，为后续的展望工作打下基础。

[1]BOLLE R M,VEMURI B C.On three-dimensional surface reconstruction methods.IEEE Trans.Pat.Anal.Mach.Intell,1985,7(4):431-441.

[2]WATSON D F.Computing the N-dimensional delaunay tessellation with application to voronoi polytopes.The Computer Journal,1981,24(2):167-172.

[3]BERARIDINI F,MITTLEMAN J,SILVA C,et al.The ball-pivoting algorithm for surface reconstruction.IEEE Trans.Virsualization Comput.Graphics,1999(4):43-72.

[4]LAWSON G L.Generation of a triangular grid with application to contour plotting[C].In:Teehnical Memorandum.Institute of Technology,Jet Pollution Laboratory,California,1972:294-299.

[5]LEE D T,SCHACHER B J.Two algorithms for eonstrueting a delaunay triangulation[J].International Journal of Computer and Information Seienees,1980(9):219-242.

[6]DWYER R A.A faster divide-and-conquer algorithm fore constructing Delaunay triangulations[J].Algorithmica,1987(2):137-151.

[7]朱站立，刘天时.数据结构（第二版）[M].西安：西安交通大学出版社，1999.

[8]PIEGL L A,RICHARD A M.Algorithm and data structure for triangulating multiply connected polyonal domains[J].Computers&Graphics,1993,14(16);23-35.