多观测列互差求中误差
2010-05-17邓永和
邓永和
(丽水学院建筑工程系,浙江丽水 323000)
1 概述
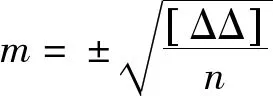
2 多观测列中误差公式推导
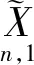
(1)
由于是等精度独立观测,故令观测值权阵为单位阵,则由最小二乘法得[2,4,5]
(2)
而观测值中误差(这里是单位中误差)为[2,4-5]
(3)
将式(1)和(2)代入式(3)得
(4)
式(4)就是本文推导的多观测列等精度观测值的中误差公式。
当n=1时,由式(3)得
(5)
式(5)就是中误差贝塞尔公式。
当r=2,即是双观测列,由式(4)得
(6)
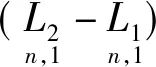
根据式(5)、式(6)和式(4)可知:中误差贝塞尔公式与双观测列中误差公式是一致的,它们可以统一于多观测列中误差公式。但是,中误差贝塞尔公式并不能严格得到[4-8],那么,它与双观测列中误差一致,或许只是一种巧合。
当r=3,即是三观测列,由式(4)得
m=
(7)
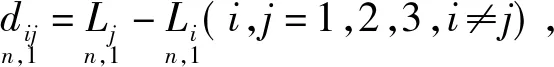
(8)

(9)
从形式上看,上式与文献[3]的式(6)不同,但可以证明它们是相等的。下面是具体证明。
[(L3-L1)-(L3-L2)]T[(L3-L1)-
(L3-L2)]-(L2-L1)T(L2-L1)=0
(10)
展开得
(L3-L1)T(L3-L1)+(L3-L2)T(L3-L2)-
(L2-L1)T(L2-L1)-2(L3-L2)T(L3-L1)=0
(11)

(12)
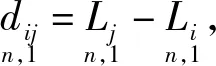
(13)
顾及文献[3]中变量di(i=1,2,3)的含义、本文的dij(i,j=1,2,3)变量的含义,以及d13+d32=d12,
由文献[3]的公式(6)可得
(14)
顾及式(12),很容易得到式(13)和(14)是相等的结论。
3 结论
文献[3]中理论推导欠妥,但它的公式(6)的结果却正确。
笔者基于最小二乘法和单位权中误差公式,推导了多观测列中误差公式、中误差贝塞尔公式与双观测列中误差公式,揭示了中误差贝塞尔公式与双观测列中误差公式是一致的,它们可以统一于多观测列中误差公式之中。
[1]覃 辉.土木工程测量(第二版)[M].上海:同济大学出版社,2005
[2]武汉测绘科技大学测量平差教研室.测量平差基础[M].北京:测绘出版社,1996
[3]赵文亮.利用三观测列互差求中误差[J].测绘通报,2009(6):26-27
[4]崔希璋,等.广义测量平差[M].武汉:武汉测绘科技大学出版社,2001
[5]於宗俦,于正林.测量平差原理[J].武汉:武汉测绘科技大学出版社,1990
[6]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,1989
[7]邓永和.中误差贝塞尔公式的推导[J].大地测量与地球动力学,2009,29(3):128-130
[8]邓永和.中误差贝塞尔公式推导的进一步研究[J].铁道勘察,2009,35(5):8-9
