基于模态法的静态电压稳定性分析

肖 盛，张建华，郭世繁

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

近年来，世界范围内发生了多起因电压崩溃引起的电网大面积停电事故。由于我国各大区域电网的互联，电压的不稳定可能会成为今后电网稳定破坏的主要因素[1-2]。为了防止事故发生，对大型电网进行电压稳定性研究是很必要的，通过分析电网的电压稳定趋势，找出电压薄弱区域，有针对性的提出预防控制措施，保证电网的安全稳定运行。目前电压稳定性分析的方法已经比较成熟，主要有灵敏度法、最大功率法、特征值分解法、潮流多解法等，这些静态分析方法简单直观，因此得到广泛应用[3-4]。

文献[5]使用改进后的Arnodli算法,可以快速计算降阶雅可比矩阵的模最小特征值和相应的特征向量,从而求出静态电压稳定裕度,以及无功功率补偿装置的安装位置及容量等；文献[6-7]考虑了发电报价、静态负荷模型和静止无功补偿装置对系统电压稳定性的影响；文献[8]利用延拓法对电力系统的动态电压稳定性进行分析，结果表明计及元件动态特性的小干扰所获得的电压稳定极限与静态分析法得到的电压稳定极限有明显的不同。文献[9]应用结构分析法对包含风电场的电力系统静态电压稳定问题进行研究[10-12]。

本文在模态分析法的基础上，提出了利用参与因子来对电网电压稳定性进行分析，以国内某一大型电网为研究对象，通过分析得到该系统中的薄弱节点、薄弱区域；并提出相应的控制措施。

1 模态法原理

假设收敛潮流的雅可比矩阵为Jr，其具有非零相异的特征值λ1、λ2…λm和相应的右特征向量U1、U2…Um与相应的左特征向量V1、V2、…Vm，由于各个特征值是相异非零的，所以与其相对应的左右特征向量是线性无关的，因此可以将注入的变化量ΔYs与状态向量的偏差量ΔX分别用Jr的右特征向量基来表示。

式中，αi、βi分别为ΔYs与ΔX的右特征向量间的标量耦合系数。

根据关系式

又因为

则可得到耦合系数间的关系

将（6）式代入（2）式得到

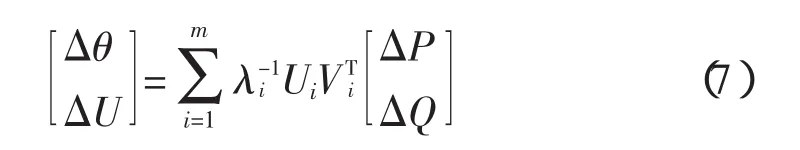
假若注入功率的变化方向为右特征向量Ui的方向，变化量的大小满足

式中，Uji为向量Ui的第j个元素，即

则该功率变化引起的状态向量的变化为

可见状态变量变化方向与功率变化的方向相同，只是其变化幅值被放大了1/λi倍，因此，λi在一定程度上反映了功率沿Ui方向变化时，对应的系统静态稳定性程度。λi愈小，所引起的状态变量的变化也就越大。同时由式(8)和式(9)可以看出：在与右特征量对应的m个可能的功率变化方向中，只有当功率方向与最小模特征值λmin对应的右特征向量Umin方向一致时，所引起的系统状态变量的变化最大。因此与最小模特征值对应的右特征向量Umin在一定程度上反映了系统最容易发生不稳定的方向。即当系统功率变化包括负荷的变化方向与Umin相同时，极易破坏系统电压稳定性[13-14]。

当系统运行工作点位于静稳边界时，其雅可比矩阵J奇异，即必然存在一零特征值，此时对于任意小的功率变动都将会引起状态变量的无限制漂移，这种情况对应于系统静态稳定的极限状态。当系统运行情况恶化时，总有一特征值首先通过零点，该特征值的模必然最小，本文称之为最小模特征值，并用λmin表示。因此可以用λmin来间接地度量全系统的静态稳定裕度[15-16]。

2 薄弱区域的确定

对于实际电力系统，仅仅求得过渡运行方式下的系统临界注入矢量和对应的临界电压矢量一般还不能满足系统运行和生产的要求，因为现有的静态电压稳定分析方法一般均假设任何一个节点或区域的电压不稳定即为全系统的不稳定。因此，有必要对系统的运行状态即临界状态作进一步的剖析：即确定哪些节点或哪些区域的电压稳定性最差,最易发生电压崩溃[17]。

在式（2）中，若取ΔP=0，ΔQ=ek，其中ek是第k个元素为1，其余元素均为0的单位列向量。即假设系统的有功注入量保持不变，仅在第k个节点上增加注入单位无功,则所引起的系统状态变量的变化为

式中定义Pki=ukivki为左特征向量vi的第n+k-1个元素。所以，第k个节点的电压灵敏度为

其中定义Pki=ukivki为第k个状态变量对第i个特征模式的参与因子,它是无量纲的纯数。

1）参与因子Pki反映了第i个特征模式λi对第k个节点电压灵敏度的相对贡献大小，Pki愈大,说明第k个节点的电压灵敏度主要由模式λi决定；

2）通过比较同一特征模式λi对不同节点电压灵敏度的贡献，就可找出与特征模式λi强相关的主要节点。假如系统以该模式失稳(λi≤0)，则与λi强相关的节点即构成了系统以该模式失稳时的失稳区域；

3）如果最小模特征值λmin>0，则与其强相关的节点即构成了全系统电压稳定程度最差或最易发生不稳定的区域。

本文计算了正常状态和稳定极限状态2种模式下的参与因子，即在这2种情况下的各个节点贡献程度。

由式（11）可以看出：特征结构分析法实质上是对传统的灵敏度判据在雅可比矩阵的特征空间中作进一步的解剖。此外，由于上述模型中同时包含了有功功率和电压相角量，所以与传统的d Vk/d Qk方法相比，本文所提出的方法更能反映电力系统的实际，因为当系统运行工作点接近静稳极限时，有功与无功间的解耦特性已不复存在[18]。

3 算例分析

以我国某区域大电网为例进行研究，该电网内有10座500 kV变电站，51座220 kV变电站，500 kV和220 kV的母线就多达223条，最大负荷为10990 MW，是一典型的受端系统。

3.1 模态法分析结果

对该电网进行建模研究，计算电网中各节点在初始状态和极限状态下的节点参与因子，表1和表2主要列出了500 kV母线节点以及部分220kV母线节点在这2种方式下的参与因子。

由以上分析结果可以看出系统在初始运行状态和极限运行状态下，其中最薄弱的节点都是1A太阳站，虽然参与因子最大的前10个节点在这2种运行状态下并不完全相同，但是它们构成的最薄弱区域却是一致的，主要是以城北500 kV变电站及其周围220 kV变电站所构成的区域，以顺义500 kV为中心的几个站构成了该区域较薄弱区域，图1大致的表示了这2种运行状态下系统中的薄弱区域和次薄弱区域。由图可以看出系统中的电压薄弱区域比较集中，并且明显的分为2个连续的区域，这有利于对该区域进行集中无功补偿，改善电压稳定性。

表1 500 kV母线初始和极限点参与因子

表2 部分220 kV母线初始和极限点参与因子

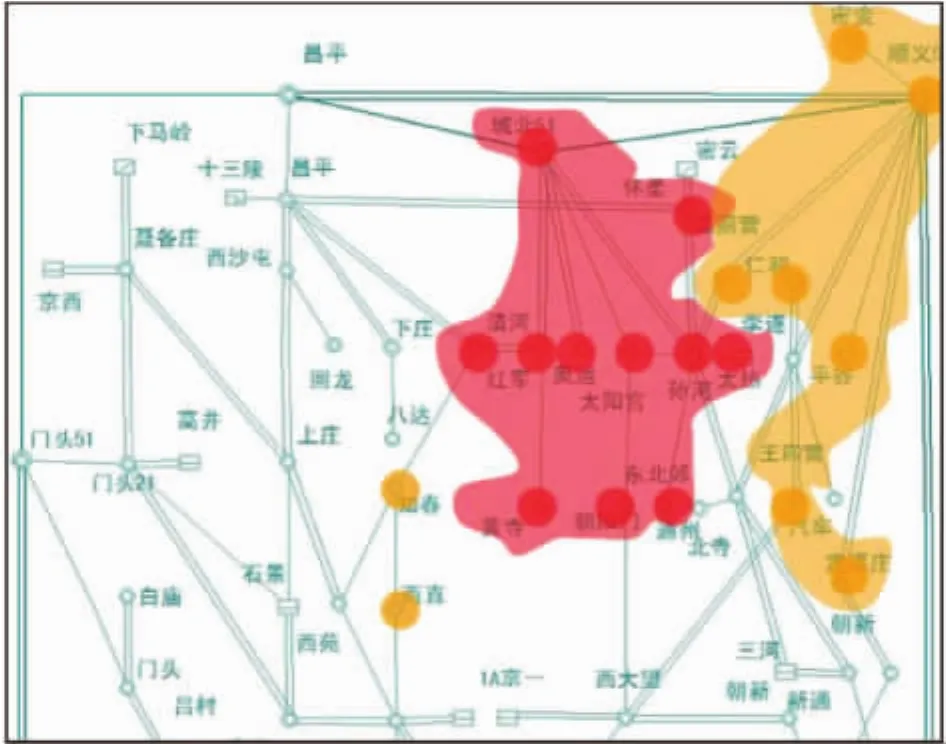
图1 模态法时系统中薄弱区域与薄弱节点（粉红色为最薄弱区域、淡黄色为次薄弱区域）

另外由上述2表可以看出在初始和极限2种状态下，220 kV的母线节点的参与因子都比500 kV的大很多，这就是说电网一旦失稳，最先崩溃的节点同其所在的电压等级没有关系，电网很有可能从低电压等级的母线最先开始电压失稳的。

3.2 与灵敏度法比较

在计算电压稳定极限的过程中，还可以计算出各母线的电压对系统总功率的变化率，即电压-功率灵敏度，根据该灵敏度由大到小也可以确定该系统的薄弱节点和薄弱区域，由于灵敏度法是基于静态潮流方程计算电压-功率灵敏度，所以该灵敏度反应的是由于系统网络特性所决定的薄弱区域节点和薄弱区域，可能与考虑发电机及其励磁系统的模态法分析结果可能有一定的差异。

图2为灵敏度分析法所得到的该算例系统中薄弱节点和薄弱区域，与图一模态法所得到的结果相比，灵敏度法所得到薄弱区域与薄弱节点明显较少些，那是因为本文模态法采用的修正潮流雅可比矩阵包含了与系统电压稳定性密切相关的各种动态元件特性，所以得出的薄弱节点、薄弱区域更为合理。

图2 灵敏度法时系统中薄弱区域与薄弱节点（粉红色为最薄弱区域、淡黄色为次薄弱区域）

4 结论

文中提出了基于模态法的静态电压稳定性分析的新方法，通过计算最小模特征值下各个节点的参与因子，来找出系统中的薄弱区域。通过对实际电网的研究结果表明，该方法简单有效，能有效的为运行控制人员提供某一时刻或者断面最有可能发生电压崩溃的节点和区域，从而可以对该薄弱区域进行集中补偿等措施，有效的改善了系统的电压稳定性。

[1] 曾纪添.电力系统无功补偿及电压稳定性研究综述[J].南方电网技术，2008,2(1):56-60.

[2] 钟清,蔡广林,张勇军,等.电力系统电压稳定的安全控制研究述评[J].南方电网技术，2008,2(5):1-5.

[3] 徐涛,张振程,任全在.基于交流电路运行特性的电压稳定裕度指标[J].电网与清洁能源,2009,25(10):38-42.

[4] 范伟,赵书强,胡炳杰.应用STATCOM提高风电场的电压稳定性[J].电网与清洁能源,2009,25(4):40-44.

[5] 孙建生，侯志俭，王承民.Arnodli算法在电力系统静态电压稳定性分析中的应用[J].电力系统自动化学报，2005,10(17):79-81.

[6] 李国庆，李小军，彭晓洁.计及发电报价等影响因素的静态电压稳定分析[J].中国电机工程学报，2008,5(28):35-40.

[7] 徐琼璟,徐政.基于PSS/E的动态无功补偿装置机电暂态仿真模型[J].南方电网技术，2008,2(5):39-42.

[8] 苏永春，汪晓明.基于延拓法的电力系统动态电压稳定性分析[J].电力系统保护与控制，2009,4(37):12-16.

[9] 马幼捷，张继东，等.特征结构分析法对风电系统静态电压稳定的研究[J].中国电力，2008,3(41):87-92.

[10] 宋伟伟，李强，袁越.双馈风电机组接入地区电网后的电压稳定分析[J].电网与清洁能源,2009,25(5):3-40.

[11] 张锋，刘洪，晁勤，等.风电接入地区电网的的静态电压稳定性研究[J].电网与清洁能源,2009,25(10):67-71.

[12] 李作红，李建华，李常信，等.风电场静态电压稳定研究[J].电网与清洁能源,2008,24(3):45-50.

[13] 冯治鸿，周双喜.大规模电力系统电压失稳区的确定方法[J].中国电机工程学报，1997，17(3):152-156.

[14] 戴宏伟,王成山,余贻鑫.基于雅可比矩阵修正模型的电压稳定频域分析方法[J].电力系统及其自动化学报，1998,10(2):20-26.

[15] 谷寒雨，陈陈.一种新的大型电力系统低频机电模式计算方法[J].中国电机工程学报，2000，20(9):50-54.

[16] A ngelidis G,Sem lyen A.Imp Roved Methodo Logies for the Calculation of Critical Eigenvalues in Small Signal Stability Analysis[J].IEEE Trans on Power System 2s,1996,11(3):1209-1217.

[17] Song H，Kim H，Lee B，et al.Determination of Interface Flow Margin Using the Modified Continuation Power Flow in Voltage Stability Analysis[J].IEE Proceedings of Generation，Transmission and Distribution，2001，148(2)：128-132.

[18] Ajjarapu V，Colin C.The Continuation Power flow：a Tool for Steady State Voltage Stability Analysis[J].IEEE Transactions on Power Systems，1992，17(1)：416-423.