用于三维傅氏轮廓术的一种自适应基频带通滤波器

雷存栋，吕银环，王汝笠

（中国科学院上海技术物理研究所 上海 200083）

用于三维傅氏轮廓术的一种自适应基频带通滤波器

雷存栋，吕银环，王汝笠

（中国科学院上海技术物理研究所 上海 200083）

介绍了傅氏轮廓术的基本原理，通过仿真与调相频谱分析，提出了一种新的自适应基频带通滤波器算法。利用此算法设计出了基频带通滤波器并用于傅氏轮廓术的位相提取。结果表明，相对于非自适应性的滤波器，使用本文设计的滤波器其三维面型测量精度可以提高5％，并且具有稳定的重复测量精度，在不受主观因素的影响下实现了实时三维面形重建。以螺纹钢面型为例进行了位相提取实验，实验中计算了面型测量精度，并与理论仿真精度进行比对与分析，得出的实验结果与理论仿真结果相一致，验证了该算法的有效性。

傅氏轮廓术；自适应基频带通滤波器；位相重建；测量精度

1 引言

用傅氏轮廓术测量三维物体，是非接触式三维测量的一个研究分支，很具有研究前景［1～4］。傅氏轮廓术的测量原理是把条纹图从空域变换到频域，在频域中去掉高频噪声和背景噪声，仅保留条纹基频；利用傅里叶逆变换把频域还原到空域，得到包含被调制信息的光强分布，再进行处理求得位相；最后，通过位相与高度的关系求出物体的高度分布，进行三维测量。从原理可见，提取基频而滤除其他噪声频率对位相的重建至关重要，所以有必要选择合适的基频带通滤波器。针对消除背景噪声，文献［5，6］提出了一种改进型傅氏解相法，该方法使用离焦的方式获得准正弦光栅，并用其投影来抑制高频分量。准正弦光栅从很大程度上抑制了高次谐波分量，可以近似看成仅剩背景分量和基频分量；同时，它采用半周期相移法消除零级背景噪声分量。从理论上讲，该方法可以很好地获得单一的基频分量，但实际测量中其它因素也会引入高级频率噪声和载波噪声，如果只是按照理论分析的要求，采用简单的二值化滤波器模板滤出正基频分量，同样会引入较大的测量误差。相应的解决办法仍然是通过人机交互的方式来改善基频的提取。

目前，实际测量系统所采用的人机交互选择基频带通滤波器越来越不适应系统的实时测量，阻碍了该系统进一步实用化的发展。而自适应基频带通滤波器算法的提出，解决了自动选择合适的基频带通滤波器的问题。另外，选取基频的单一频谱成分时，被测物体高度斜率的变化将超过一定范围，进而引起光谱成份的重叠。使用人机交互选择基频带通滤波器，由于受到人为主观因素的影响会产生测量误差，但是自适应基频带通滤波器算法对该问题有所改善。

针对以上问题，本文分析了傅氏轮廓术（Fourier Transform Profilometry，FTP）的测量原理，基于调相频谱的计算机仿真，提出一种新的自适应基频带通滤波器算法。将该算法应用于频谱测量并进行了理论仿真，研究了该算法相对于原来的人机交互方法对测量精度的影响。最后，将该算法用于实际测量，对实验的结果与仿真的结果进行对比，给出了对比结果。

2 傅氏轮廓术的基本原理

图1所示的相交轴系统中，两光轴交于参考面上一点O。R为参考平面，EC、EP分别为CCD相机和投影仪的入瞳和出瞳光心，间距为d，两光心连线与参考平面平行，与参考面距离为L，CCD相机光轴垂直于参考平面。若Ronchi光栅的栅线方向垂直于x轴，则当一束光投射到被测物体表面上时，像平面上观察到的变形条纹像为

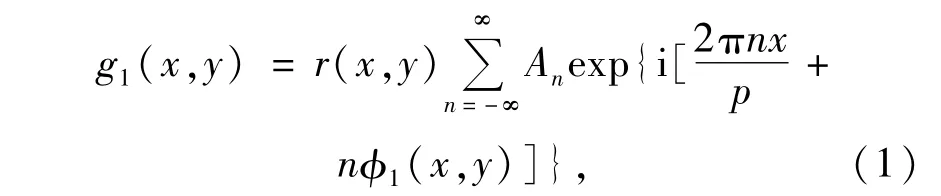
其中，p为空间载波周期，r（x，y）是物体变形面分布的反射率，An为各次谐波的对比度，φ（x，y）为物体高度分布引起的位相调制。

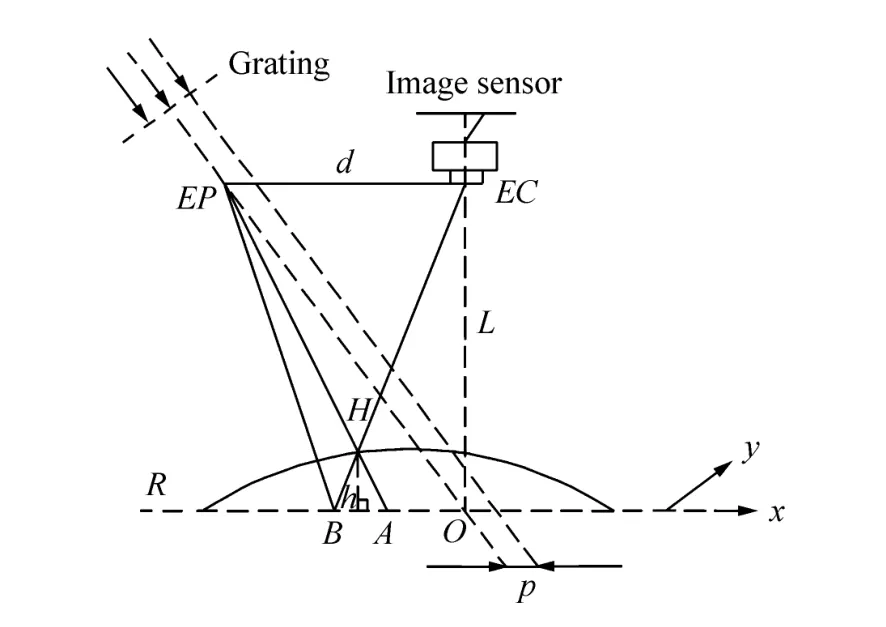
图1 交叉光轴系统Fig.1 Cross-optical axis system

当参考面上没有被测物体时，像平面上观察到的变形条纹像为

其中φ0（x，y）为参考面上投影光栅的初始位相值。

将式（1）沿x方向做一维傅里叶变换可得

其中，f0＝1/p为参考面上的空间基频。从式（3）可见，变形光栅模式中包含零频、基频以及更多高级次分量。如果只滤出基频分量，需要设计基频带通滤波器，通过该滤波器只保留正基频成份，进而进行傅氏逆变换后的光场分布为

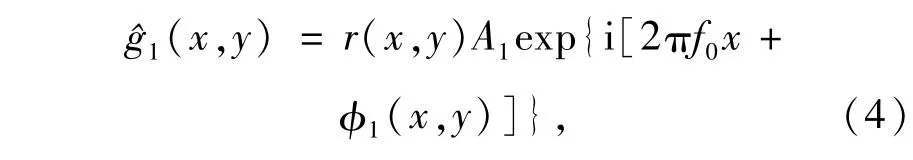
对式（2）进行相同的运算可得

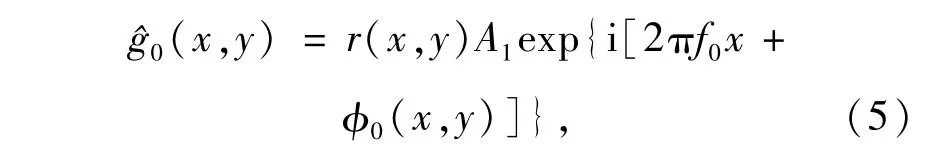
由高度造成的位相调制Δφ（x，y）为

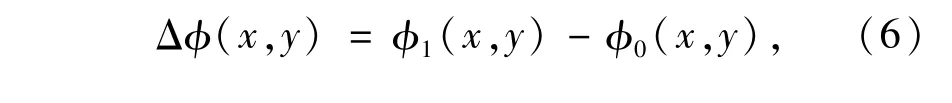
这一位相可以通过式（4）和式（5）计算得到

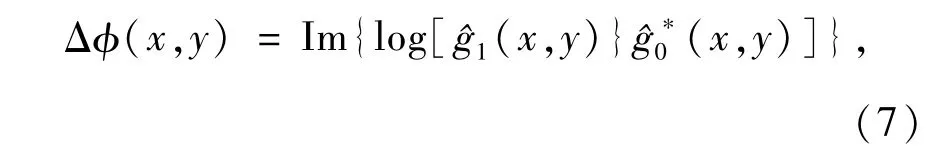
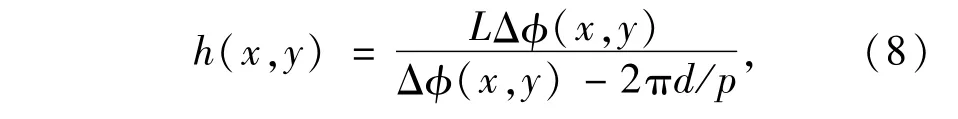
所以，基于该技术的三维测量原理的最基本问题是解调出位相分布Δφ（x，y），然后根据系统标定和式（8）对待测物体进行三维精密测量。

3 调相频谱的仿真

基于FTP技术对三维物体进行测量时，使用一个具有空间基频为f0的光栅作为载波，对三维物体的高度信息进行位相调制，调制后变形光栅模式如式（1）所示，其局部空间频率类似于调频信号中的瞬时频率［7，8］，定义如下

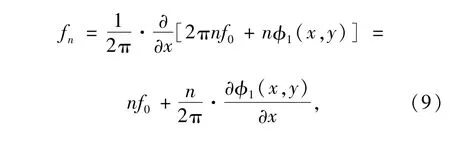
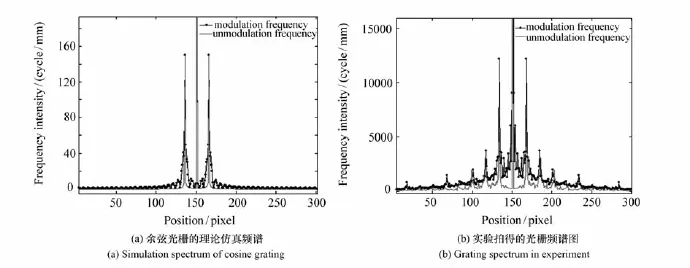
图2 理论仿真和实验获得频谱Fig.2 Spectra of grating from simulation and experiments

从式（9）中可见，当空间基频f0不变时，位相调制也会引入局部空间频率的变化，使得各级频谱被展宽。为了说明调制频谱的变化，进行如下计算机仿真。实际测量中，载波光栅采用余弦形式，主要优点体现在式（9）中n＝±1，也就是说，频谱中仅包含正负基频，相对于其他形式的光栅，更易于提取正基频。对余弦光栅以及其变形模式的仿真结果如图2（a）所示，可见由于位相调制项的引入，局部空间频带被展宽，背景噪声信号的零级频谱产生了混叠现象，而提取正基频时需要把零级频滤除掉，所以基频带通滤波器的设计需要满足相应的要求。在实际测量中，由于受到多种因素的影响，会引入更多的噪声信号，频谱的混叠现象会更严重。在对螺纹钢测量的实验中，所采集的变形光栅模式如图6（a），其频谱如图2（b）所示，图2（b）与图2（a）相比，频带展宽更为明显，并且还出现了高频噪声。因此，实际测量中基频带通滤波器的设计非常关键，其基本要求是：首先，必须滤除背景噪声和高级频谱噪声；其次，要尽可能少地丢失有用信息，这样才能有效地提高测量精度。从图2（b）可见，滤波器带通过窄会丢失有用信息，过宽会引入噪声信号。通过人机交互方式来选择滤波器，要多次反复试用，才可以逐次逼近较为合理的滤波器。这样不但耗时较长，还受人为主观因素的影响，很难实现工程化和实用化，并且不能满足实时化的需要。为了解决该问题，本文提出自适应基频带通滤波器算法，应用该方法来提取基频，进行位相面形的重建。另外，在实际测量中，参考面选取的变化，会引入被调制物体面上的光栅空间基频f0的变化，频谱图中基频的位置会相应发生变化，这样基频带通滤波器的带通只有做相应的变动，才可以提取出所需要的频带。因此，提出自适应的基频带通滤波器更有实际意义。

4 自适应滤波器算法

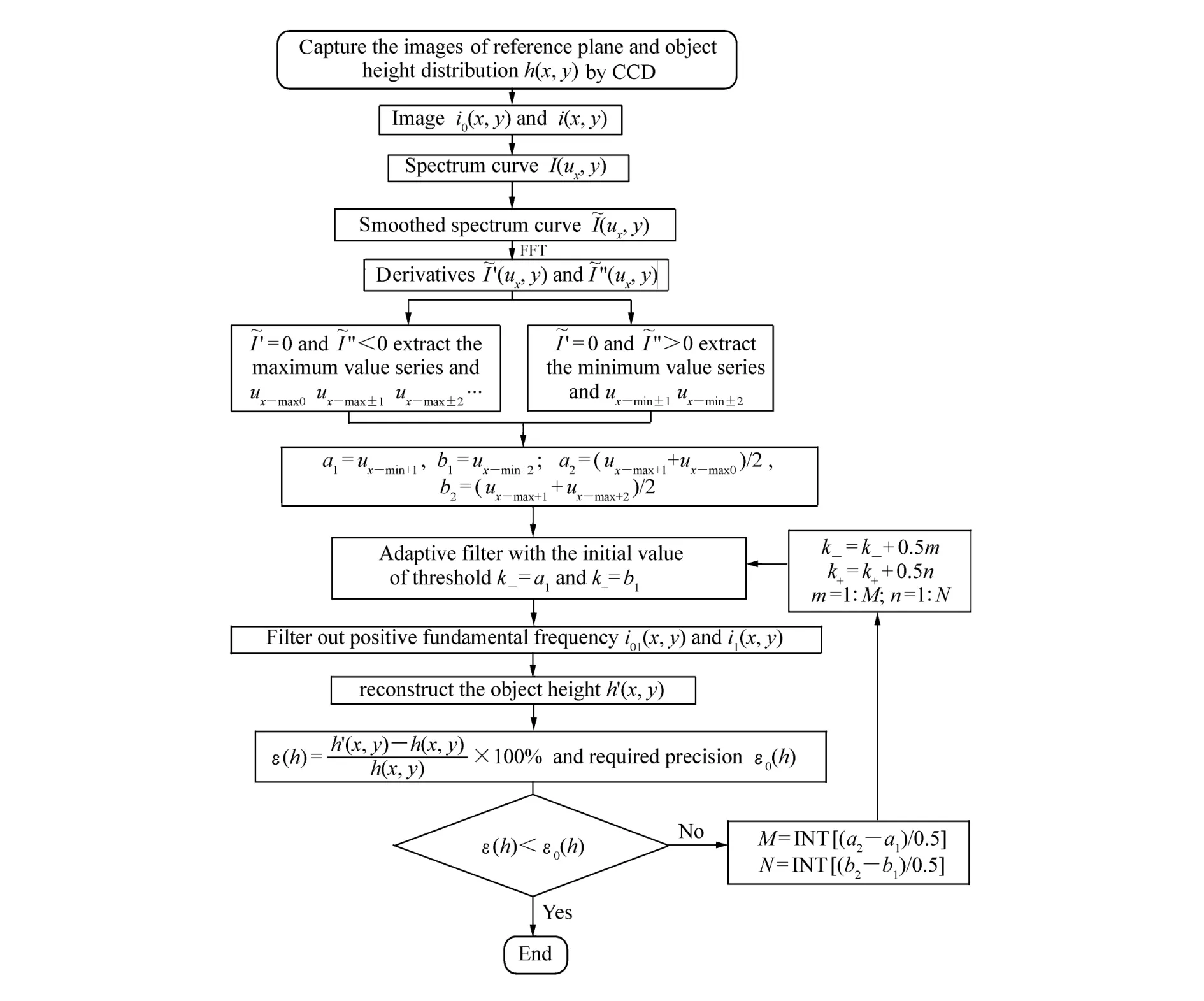
图3 自适应基频带通滤波器的算法流程图Fig.3 Flow chart for MFBF algorithm

在实际应用中，基于傅氏轮廓术进行三维测量或者建模，必须满足精确性和实时性要求，尤其是在工业自动化生产过程中，要达到在线测量的要求，而用人机交互的方式显然无法满足。由于调相频谱的扩展以及实际测量中光栅基频f0的变化，要满足实际的需要，必须准确、快速地提取出包含三维位相信息的基频，从而重建出较为精确的三维物体面形。本文通过对螺纹钢肋径的实际测量，提出一种自适应基频带通滤波器算法，利用该算法基本上实现了较为精确的实时性的三维测量。

设计自适应基频带通滤波器的关键是定出基频频带的边缘阈值，而该算法的建立是基于极值与反馈理论。首先，求出零级、一级和二级的极值，正基频的左阈值一定会介于零级与一级极大值之间，并且在一级极小值附近；右阈值一定介于一级与二级极大值之间，并且在二级极小值附近。然后，根据精度的要求，通过反馈逐步迭代定出符合要求的阈值，从而设计出自适应基频带通滤波器。算法流程如图3所示，首先采集图像信号，然后经过沿x方向进行一维傅里叶变换，获取沿x方向的一维频谱曲线，并对该曲线进行平滑与拟合处理，得一平滑连续包络曲线，再对该曲线进行求导，分为一次求导和二次求导。通过极值理论，判断出零级极大值，一级极大值，二级极大值，一级极小值，二级极小值等等。最后，设定a1和b1为滤波器阈值k-和k+的初始值，制作出基频带通滤波器，并引入傅氏轮廓术进行位相解调，重建物体的高度分布函数h′（x，y），高度测量精度如式（10）给出。将重建精度与所需精度进行比较，如果满足要求则结束；否则，阈值k-和k+分别在a1和b1与a2和b2之间变动，直到重建精度满足要求为止。

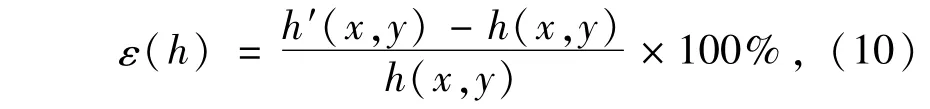
使用这种算法设计出的自适应滤波器，可以使基于傅氏轮廓术的三维测量系统或者建模系统实现完全的自动化与实时化。

5 理论仿真与实验分析

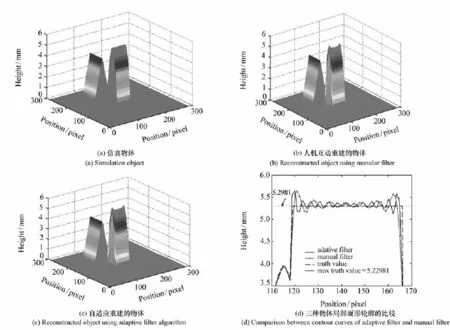
图4 三维物体的仿真与重建Fig.4 Simulation and reconstruction of3D object

取余弦光栅基频f0＝4l/mm，几何结构参数L＝2 000mm，d0＝148mm，相机采样间隔Δx＝7μm，对如图4（a）所示的物体进行仿真，使用人机交互的方法制作基频带通滤波器进行物体重建，结果如图4（b）所示；采用自适应滤波器算法制作滤波器重建结果如图4（c）所示。比较两种方法重建的物体与原物体的局部面形轮廓曲线如图4（d）所示。分析图4可见，人机互动方法所重建面形的最大边缘毛刺误差为6.43％，平均误差为0.23％；自适应算法重建面形的最大边缘毛刺误差为6.3％，平均误差为0.22％。自适应滤波器与人机交互选择，基频带通滤波器相比，对物体面形的重建精度基本上一致，但是利用人机交互方法时，由于受主观因素的影响，测量精度不够稳定，而自适应方法克服了此缺点。在FTP技术中，虽然同样无法在面形重建中克服高度梯度为无穷大的问题，即无法完全避免边缘毛刺误差，但平均误差基本上可以满足精度要求。

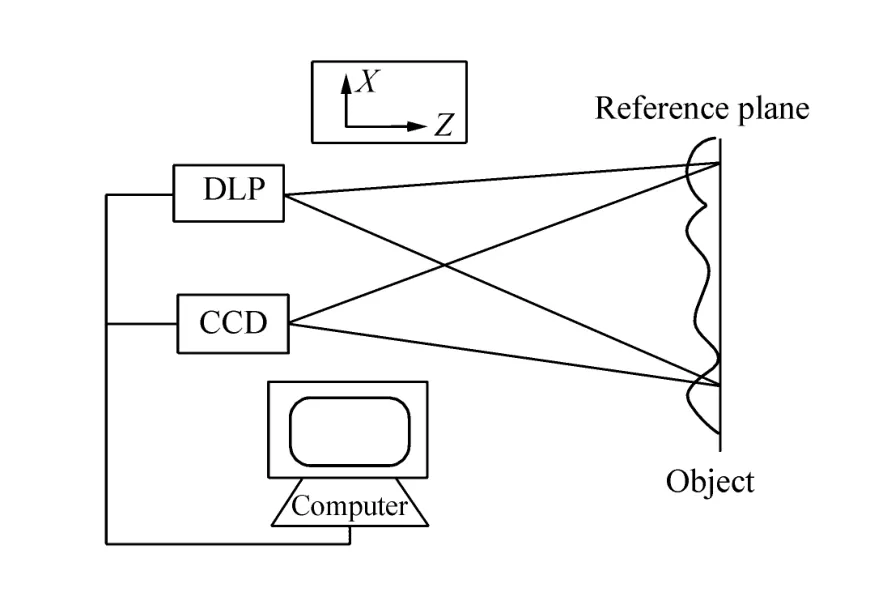
图5 三维测量系统原理图Fig.5 Principle of experimental setup

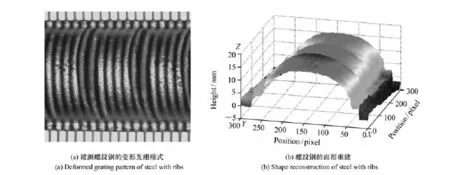
图6 螺纹钢的变形光栅模式与面形重建Fig.6 Deformed grating pattern of steelwith ribs and its shape reconstruction

表1 两种方法测量结果与接触式真实数据值的比较Tab.1 Comparison between measurement results of two algorithms and truth values

用如图5所示的实验装置对螺纹钢进行测量［9］，采集的螺纹钢变形光栅模式如图6（a）所示，使用本文提出的自适应基频带通滤波器算法进行面形重建结果如图6（b）所示。首先，使用人机交互选择基频带通滤波器方法进行面形重建，通过多次反复调整滤波器阈值，重建出了符合精度要求的螺纹钢面形。然后，把精度要求输入计算机，选定内径精度要求为ε0（h）＝0.75％作为面形重建的标准，使用自适应算法对螺纹钢面形进行重建。将两种方法所重建的物体面形结果进行对比如表1，绘出了两种方法的径向高度分布曲线，对比结果如图7。从表1及图7中可见，自适应基频带通滤波器算法能够满足测量精度与实时性的要求，结果基本与人机交互方式所达到的测量精度接近或略高。

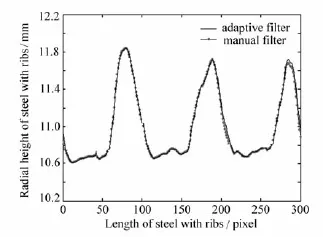
图7 基于自适应滤波器与人机交互滤波器所重建的螺纹钢径向高度分布曲线的比较Fig.7 Comparison between restored radial heights based on adaptive and manual filters

6 结论

本文针对螺纹钢肋径的测量提出了新型自适应基频带通滤波器算法。该方法克服了人机交互方法的局限性，能够在不降低测量精度的情况下，自动快速地对三维物体进行面形重建，实现了测量系统的实时性，克服了人为因素的影响，测量结果更具有客观性且测量精度稳定。将其与人机交互方式所获得的仿真与实验结果进行对比，证明了自适应基频带通滤波器的优点，对傅氏轮廓术的进一步实用化具有一定的意义。

［1］TAKEDA M，MUTOH K.Fourier transform profilometry for the automatic measurement of 3-D object shapes［J］.Appl.Opt.，1983，22（24）：3977-3982.

［2］TAKEDA M，INA H，KOBAYASHIS.Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry［J］.JOSA，1982，72（1）：156-160.

［3］GREEN R J，WALKER JG，ROBINSON DW.Investigation of the Fourier-transform method of fringe pattern analysis［J］.Opt.Lasers Eng.，1988，8：29-44.

［4］葛东东，王淮生，宋家友.光栅投影三维轮廓测量技术分析及进展［J］.上海电力学院学报，2005，21（4）：378-382.

GE D D，WANG H SH，SONG JY.The analysis of3D profilometrymeasurement by grating—projection and its advancement［J］.J.Shanghai University Electric Power，2005，21（4）：378-382.（in Chinese）

［5］LI J，SU X Y，GUO L R.Improved Fourier transform profilometry for the automatic measurement of three-dimensional object shapes［J］.Opt.Eng.，1990，29（12）：1439-1444.

［6］毛先富，陈文静，苏显渝.傅里叶变换轮廓术新理论研究［J］.中国激光，2007，34（1）：99-104.

MAO X F，CHENW J，SU X Y.Analysis on an improved Fourier transform profilometry［J］.Chin.J.Lasers，2007，34（1）：99-104.（in Chinese）

［7］DOWNING J J.Modulation Systems and Noise［M］.Englewood Cliffs：Prentice-Hall，1964.

［8］魏升，刘南生，刘明友，等.基于傅里叶变换轮廓术的物面相位提取［J］.南昌大学学报（理科版），2007，31（3）：260-263.

WEISH，LIU N SH，LIU M Y，et al..Phase withdraw of a 3-D smallobject shape base onfourier transform profilometry［J］.J.Nanchang University Natural Sci.，2007，31（3）：260-263.（in Chinese）

［9］吕银环，王汝笠，吴航行.等.基于改进型傅氏变换轮廓术检测螺纹钢肋径［J］.光学技术，2004，30（3）：299-302.

LV Y H，WANGR L，WUH X，etal.Measurement for the rib diameter of thread steelbased on the improved fourier transform profilometry［J］.Opt.Technique，2004，30（3）：299-302.（in Chinese）

Adaptivemain frequency bandpass filters used in Fourier transform profilometry

LEICun-dong，LÜYin-huan，WANG Ru-li
（Shanghai Institute of Technical Physics，Chinese Academy of Sciences，Shanghai200083，China）

The basic principle of Fourier Transform Profilometry（FTP）is introduced，then a new Adaptive Main Frequency Bandpass Filter（A-MFBF）algorithm is proposed based on the simulation resultof phasemodulation frequency spectrum.The proposed algorithm is used to design the A-MFBF to filter out the main frequency and reconstruct the phase of a measured object.Results show that the precision of 3-D measurement system can be improved by 5％relative to that of the average ones，and itsmetrical precision can be repeated steadily.The real-time 3-D shape reconstruction is implemented by proposed A-MFBF without effect by subjective factors.Furthermore，a experimentof reconstructing phase for the steelwith ribs is carried out，and the precision of reconstructedmeasurement is calculated and analyzed.The results show that the precision from the theoretical simulation is in good agreementwith the experimental results，which demonstrates the validity of the algorithm.

Fourier Transform Profilometry（FTP）；Adaptive Main Frequency Bandpass Filter（A-MFBF）；phase reconstruction；measurement precision

2010-01-11；

2010-03-13

1674-2915（2010）03-0245-07

TP391；TN713

A

雷存栋（1971—），男，江西人，硕士，主要从事光电信息处理和模式识别方面的研究。E-mail：leicd2001@yahoo.com.cn