蕴涵理论与一致性原则
2010-05-06杨福荣周祯祥
杨福荣,周祯祥
(1.华南师范大学政治与行政学院,广东广州 510631;2.宝鸡文理学院政法系,陕西宝鸡 721016)
蕴涵理论与一致性原则
杨福荣1,2,周祯祥1
(1.华南师范大学政治与行政学院,广东广州 510631;2.宝鸡文理学院政法系,陕西宝鸡 721016)
蕴涵与一致性原则是逻辑系统不可或缺的,蕴涵是逻辑系统的表述方式,而一致性是逻辑系统成立的基本条件,蕴涵与一致性存在密切联系。无论是罗素实质蕴涵,还是刘易斯的严格蕴涵,都出现了相类似的“蕴涵悖论”,其原因是违反语言常识的直观、违反了一致性原则的缘故。所以,正确有效地推理离不开对蕴涵和一致性原则的讨论。
蕴涵悖论;严格蕴涵;一致性
一
逻辑学已经形成共识:蕴涵是一个二元逻辑联结词,它是对自然语言“如果A,则B”的逻辑抽象,假言的充分条件命题作为其存在形式,表达的是具有充分条件关系的前后件之间的真值推理关系。对此,我们可以从古希腊的斐洛蕴涵中得到引证。斐洛蕴涵为“完善的条件命题是一种并不开始于真而结束于假的条件句,例如当白天时,我在谈话,陈述句‘如果是白天,我就在谈话’”①。由此可以看出,古希腊的学者当时已经认识到,充分条件假言命题“如果A,则B”的肢命题存在四种可能的真值组合:前件真后件真,前件假后件假,前件假后件真,前件真后件假。
蕴涵一直都是逻辑学讨论的重要的热门话题,其重要性表现在两个方面。其一,有关蕴涵的讨论历史悠久。最早的蕴涵研究可以追溯到亚里士多德,他在《工具论》中将三段论式应用蕴涵式,之后的麦加拉学派斐洛专门研究了蕴涵式,对此塔尔斯基就明确指出“斐洛(philo)在逻辑史上大概是第一个传播了实质蕴涵用法的人”②。其二,逻辑学发展离不开对蕴涵问题的研究。整个逻辑学的发展离不开对推理问题的研究,蕴涵式与推理式紧密联系,存在诸多的相似性和区别。金岳霖认为“蕴涵的问题太大,牵扯出来的问题太多”③。没有蕴涵就没有推理,蕴涵是推理的必要条件。
相比斐洛蕴涵而言,现代时期逻辑对蕴涵的研究当然是有所丰富和发展的。其中弗雷格、皮尔士等逻辑学家对蕴涵做出了独到的见解,普遍认为蕴涵与推理作为同一系列的概念来应用。也就是说,蕴涵可被看成是由一个命题推出另一个命题的推理关系,彰显了蕴涵所能表述的最为直观的含义。
罗素在《数理哲学导论》中提到:“为了能够正确地推论出一个命题真,我们必须知道某个别的命题真,并且在二命题间有一种称作是‘蕴涵’的关系,即前提‘蕴涵’结论。”④在此之后,罗素在《数学原理》中讨论类型论时使用“实质蕴涵”概念来命名斐洛蕴涵。罗素是用“A⊃B”表示“A实质蕴涵B”或“如果A,则B”的,其中“⊃”表示实质蕴涵,于是他把实质蕴涵定义为:

(ⅰ)公式表明“A实质蕴涵B”可以定义为“A是假的或者B是真的”。这个定义从真假值的角度考察了否定、析取和蕴涵三种命题间的关系。其中任何一种关系都可以由另外两种关系表示。这样“A实质蕴涵B”就可以等价为¬A和B的析取(¬A∨B),也可以表述为或者说A是假的或者说B是真的。当然,¬A∨B也可以表示为合取的否定:¬(A∧¬B)。从中可以看出,以上三种关系的真假值都是只依赖于它们命题变元的真假值。
由此可以得知,斐洛蕴涵应该是最先表达了实质蕴涵的用法。而罗素对实质蕴涵的研究是建立在纯粹的真值判定基础上的,由于它能表露出明显的方便性和简单性,很快被逻辑学界接受,成为经典命题演算系统的基础。
但令人遗憾的是,罗素定义蕴涵的方式却产生了“与普通推论方式大相径庭”⑥的结论。例如,从(ⅰ)定义公式可知:
(1)只要A为假,A⊃B就是真的;
(2)只要B为真,A⊃B就是真的;
我们可由前提命题应用析取引入规则可得B⊃A∨B,如果用¬A替代A,变换可得:

可再用A⊃B代入上式可得:

该公式表明:一个真命题被所有命题所蕴涵。
同理,我们仍然可由B⊃A∨¬B进行变换。其中的B用¬B代入,得到:
¬B⊃A∨¬B,因而可得到:

该公式表明:一个假命题蕴涵着任何命题。
借助实质蕴涵的真值定义,我们还可以得到

其中(ⅳ)式意味着任何两个命题之间都有蕴涵关系;(ⅴ)式意味着任何命题或者蕴涵另外任何命题,或者蕴涵另外任何命题的否定。⑦
在逻辑史上,由实质蕴涵导出的(ⅱ)、(ⅲ)、(ⅳ)、(ⅴ)等公式被称为“实质蕴涵悖论”。对此,人们可以看到有些蕴涵探索者的足迹。
出现蕴涵悖论的主要原因是把符号“⊃”作为“蕴涵”来解释,如果“A⊃B”的解释少于“¬A∨B”时是不会出现悖论的。因为数学原理的逻辑系统是演绎系统,新的结论都是来源于最初的前提;但是我们用缩写形式“A⊃B’”来表示“¬A∨B”,其结果是不能恰当地反映蕴涵关系的。⑧
对于以上观点,我们可以表示认同,但是这样的认识只是表明了实质蕴涵悖论产生的表层原因,缺乏更深层次的表述。而对于实质蕴涵,还需要人们锲而不舍地深入探究。美国逻辑学家C.I.刘易斯就是其中的一位学者,他不但指出实质蕴涵不符合通常意义的“如果A,那么B”句式,还提出了新的蕴涵形式——严格蕴涵,从而促进了蕴涵理论的研究及其发展。
二
刘易斯一开始就对《数学原理》中的逻辑“深感困惑”⑨,他坚决反对罗素实质蕴涵,他在1912年发表《蕴涵与逻辑代数》说:把“凯撒不死”这个命题看做是蕴涵“月亮是由绿奶酪所做成”或者认为“巴黎在法国”这个命题由“伦敦不在英国”这个命题所蕴涵,这实在是荒唐,而实质蕴涵实际上就是在作这种荒唐的推理。⑩
可见,刘易斯已经认识到,实质蕴涵既不符合自然语言中“如果,则”的原有意思,也不符合蕴涵的逻辑涵义;相反的,实质蕴涵系统却隐含了形如实质蕴涵悖论等这些无用的推理模式或近似荒唐的悖理的模式。刘易斯认为,实质蕴涵悖论之所以能够出现,不仅是“因为‘蕴涵’被具体应用到代数中”(11)而脱离了语言实际运用的视域,“缺失”(12)一致性的缘故。因此,为了避免蕴涵悖论,实质蕴涵“必须经过某种审查”(13),既要求蕴涵的意义必须建立在更加直观的基础上,还要经历对“自我一致”的选择(14)。只有坚持了以上两点,我们才能消除那些无用和荒唐的推理模式,进而使逻辑学发展更加符合人们通常意义上的语言直观的要求。
刘易斯在《蕴涵和逻辑代数》(15)论文中区分模态逻辑“可能性”概念时首次提出了“严格蕴涵”概念。他表示:“说到◇A,‘A是可能的’或者‘A是自我一致的’虽然还没有在一些定理中出现,但是我们可以着手去做,只要有可能的话,我们完全可以把‘A≺B’作为‘初始的概念’而用来代替◇A”(16)。
这样我们就可以得到如下的关系:

由于命题间的一致性与此存在密切联系,为此,刘易斯在1932年《符号逻辑》中推出了一致性的思想:当我们说两个命题是“一致的”,我们的意思就是“无论其中哪一个命题做前提,我们都会推出另一个命题是假的”这是不可能的。如果我们打算用A≺B表示“由A可以推出B”的话,“A和B是一致的”可以定义为:AoB=df¬(A¬B)。(17)
在这个定义中,符号“AoB”表示A和B是一致的,“≺”表示“严格蕴涵”。这个定义所导出的性质,完全可以作为通常意义的‘蕴涵’和‘一致性’以及函数‘AB’和‘AoB’之间相协调的一个判定标准。(18)整个定义式表明命题间的一致性可用严格蕴涵进行表述。对此,刘易斯说:“这个定义所显现的严格蕴涵的性质是完全符合通常意义上‘蕴涵’和‘一致性’以及概念‘AB’和‘AoB’的。”(19)从上式可以看到,严格蕴涵“AB”完全符合日常语言的自然用法,也是满足他的一致性要求:从命题A推出命题B的否定,即,推出¬A是不可能的。
其实我们应该知道,逻辑一致性是任何理论包括公理系统所必须满足的条件,现代逻辑把一致性规定为无矛盾性。人们要构造一个逻辑演算S,总是要求S在解释以后不会出现逻辑矛盾,即不会断定两个互相矛盾的命题。如果一个逻辑演算S满足了这个要求,我们就说S有一致性,或是S是一致的;就一致性的本质而言,一致性就是在一个逻辑系统中导不出逻辑矛盾。
刘易斯的一致性概念与上述逻辑系统的一致性概念非常相似,而且比上述一致性概念有更宽泛的含义。因为他的一致性概念既与逻辑矛盾紧密相关,也与模态基本范畴中的可能概念紧密相关。令人遗憾的是,刘易斯只是把一致性概念看做是一种关系,即是两个命题之间的关系,讨论范围略显狭窄,并没有用一致性原则解决更多的逻辑难题。
为了进一步挖掘严格蕴涵的逻辑性质,我们还要用到“自我一致性的假定”(20):¬(AoA)≺¬(AoB)。
如果A是自我不一致的,那么A与任何其他命题也是不一致的,或者A是自我不一致的严格蕴涵着A与任何其他命题是不一致的。
如果A是不可能命题,那么A与任何命题都是“不一致”的,例如¬A。之后刘易斯认为“A严格蕴涵B”可表示为:B能从A正确地推出来。他用“¬◇”表示不可能,用“¬”表示否定,并把后者定义为:
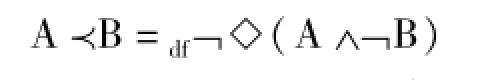
刘易斯在《符号逻辑》中还推出了定理11.02:

根据(ⅵ)(ⅶ),对AoB=df¬(A≺¬B)变形得:

进而得到17.12:

(ⅷ)公式表明了严格蕴涵与一致性具有等价关系。
因此,如果A是不可能命题,那么A与任何其他命题是不一致的。如果是¬B,那么根据(ⅷ)公式,可得到¬◇A⊃(AB)。也就是说,不可能命题严格蕴涵着任何命题。这就是定理19.74(23):¬◇A·AB(如果A是不可能的,那么A严格蕴涵任何命题B);同理,如果B是必然命题,那么¬B就是不可能的命题,因此¬B也会是与任何命题A不一致的,同样的结果就是□A⊃(BA)。这样必然命题被任何命题所严格蕴涵。这就是定理19.75:¬◇¬A·BA(如果A是必然的,那么任何命题B严格蕴涵A)。
我们由此也得到了严格蕴涵悖论,这是与实质蕴涵相同的结果,从而也引发了另一种相干蕴涵理论的发展。
三
蕴涵悖论的确令人为难。但刘易斯认为,严格蕴涵悖论与实质蕴涵悖论却是不同的。虽然严格蕴涵悖没有被避免,但重要的是,我们可以“忽视这些悖论的”(24)。因为严格蕴涵关系不但精确地表达了有效推论关系,而且也满足了语言的实践需求。在这个意义上,刘易斯认为“严格蕴涵系统可被看做是为提供推理的前提和规则成为逻辑调查所急需”(25)。
或许刘易斯把严格蕴涵悖论作为定理(26)有其他目的,这应该算是刘易斯在为严格蕴涵悖论寻求的辩护。值得一提的是,这些所谓的蕴涵悖论都是从那些已被认为有效的和为真的前提中推出的。(27)这的确令人感到困惑。例如,在逻辑学中存在如下的经典推理规则:
(2)A(1)的合取分离
(3)¬A(1)的合取分离可得
(4)A∨B(2)的析取引入
(5)B(3)(4)的否定肯定式
由此我们可以看出,无论是实质蕴涵还是严格蕴涵等都是具有存在的合理性,它们都是逻辑本性使然。因为一种推理是否正确,不仅要看推理形式的逻辑性,而且也要从思想内容上分析其前提与结论命题意义的关联性。刘易斯试图通过悖论的合理性来表明他所提出的命题间的严格蕴涵的定义比实质蕴涵更好,相比实质蕴涵而言,严格蕴涵的定义更加接近于人们对蕴涵定义满意的要求。由此可见,严格蕴涵相比实质蕴涵要求多得多。所以,“严格蕴涵的推演能力弱于实质蕴涵”(278)。刘易斯就此也发表过自己的意见:“在推出有效结论方面,实质蕴涵是一无所用的,……任何推理可在其中基于实质蕴涵被做出的情形恰恰就是它在其中应该符合于(并且被获知符合于)由A到B的内涵的或严格蕴涵的情形。这就等于说这一推理的真正基础是严格蕴涵。‘A严格蕴涵B’正意味着‘A的真与B的假是不相容的’。”(29)
从发展的观点看,相对于罗素的实质蕴涵而言,刘易斯提出辩论来反对罗素缺少说服力,他的严格蕴涵并没有必然的、更加正确,也并不是对实质蕴涵的不带任何偏见的批驳;但他却给我们指明了逻辑与常识之间的确存在明显的差异。蕴涵作为对自然语言“如果,则”的逻辑抽象,任何时候都不可能离开常识的直观性而不顾。换句话说,对于一个具体的命题,其前后件之间是否存在蕴涵关系,既要从逻辑形式上考察,也要从思维内容上看其关联性。实质蕴涵和严格蕴涵的共同特征表明它们并没有完全准确地表达命题间的条件关系,每一种蕴涵都只表达出命题间的一种关系。实质蕴涵只表达出“命题A、B之间不能出现A真B假的情形”;命题A与B之间的严格蕴涵关系只表达出“命题A实质蕴涵B与另外命题C∧D蕴涵C是相同的”。例如根据实质蕴涵的定义,“2+2=5”这个命题应该蕴涵着命题“雪是黑的”,“2+2=4”将为命题“雪是黑的”所蕴涵。从常识上来分析可以看到,命题“2+2=5”、“2+2=4”都分别与命题“雪是黑的”的内容是互不联系的。因此人们根本无从断定它们存在真假制约关系。如果真的需要强行撇开内容上的关联而纯粹考虑命题间真假关系的话,它们明显地缺乏直观上令人相信的理由,其结果必定是令人难以接受的,其结论也必然是不正确的。
因此,我们如果要真正了解严格蕴涵的性质,必须要把严格蕴涵和实质蕴涵区别开来。(30)刘易斯在1914年发表论文《严格蕴涵的演算》就谈道:“实质蕴涵和严格蕴涵都是自我一致的数学系统;但是它们却是被应用到不同的领域中。实质蕴涵是被应用到那些所有的可能真的领域;而严格蕴涵却是拥有比实质蕴涵更加广泛的应用范围。”(31)
实际上,罗素与刘易斯最大的区别在于,罗素是从外延逻辑的角度提出实质蕴涵的,属于经典逻辑的系统,他的《数学原理》的整个结构就是以实质蕴涵为基石的;而刘易斯是外延逻辑的研究者和批判者,他曾表示“由于显而易见的原因,推理可能建立于其上的惟一一种蕴涵关系就是这种内涵或严格的蕴涵”(32)。可见,刘易斯是侧重于从内涵逻辑的角度讨论严格蕴涵的,他还较为系统地发展了以严格蕴涵概念为基础的现代模态逻辑。这些足以说明严格蕴涵是属于非经典逻辑系统的。刘易斯认为“蕴涵并不是这样一些孤立的命题的一种属性,而是系统的属性”(33)。
逻辑系统的一致性已成为系统存在的客观依据。刘易斯对蕴涵理论坚持用一致性原则加以分析却是逻辑学一直以来坚持的根本研究方法。既然蕴涵理论产生了蕴涵悖论,追根溯源,这是由于它们都违反了逻辑一致性的要求,为此我们必须构建蕴涵的一致性的条件。而我们所确定一致性与逻辑矛盾是完全不等同的两个概念。一致性是比逻辑矛盾更宽泛的一个概念,不一致是逻辑矛盾产生的先决条件,逻辑矛盾是不一致的外在表现。两个命题是一致的,也就是说这两个命题都是真的。另外,如果两个命题是一致的,那么它们互相蕴涵的。但是也会存在可能两个命题既是互相蕴涵的又是不一致的。只有当两个命题都是假的时候会出现这种情况,例如:“月亮是用绿奶酪做成的”和“法国在中国的东面”就是互相蕴涵的。它们也是由于都是假的而是不一致的。
但是,刘易斯区分实质蕴涵和严格蕴涵的思想源自于他非常重视行动,他主张:“逻辑原则将服从于那类可称为实用的一般标准,而在经验证实派不上用场、逻辑‘必然性’本身又不够用的情况下,我再也找不到除此之外的任何意义上的终极标准了。”(34)可见,刘易斯过高地估计了行动的作用,犯了与其他实用主义者共同的错误。但是对于整个逻辑学发展来说,刘易斯有能力给予有关自己观点的解释。他创立的严格蕴涵是一种对罗素逻辑的增补,的确称得上是一种进步。刘易斯对严格蕴涵和必然性的分析成为现代模态逻辑创立的契机,也促成了不同逻辑系统的更替和多种逻辑形态的并存。未来的逻辑研究仍然是要为我们提供一种正确的推理规范。当我们以真命题为前提,就会产生别的真命题为结论。也正是因为“蕴涵悖论”这种违反人们的直观常识的结论出现,才引发逻辑学界对蕴涵理论的深入探讨。所以,逻辑学的繁荣和发展与对蕴涵理论的理性思考分不开的。
注 释:
① 张家龙译,威廉·涅尔,玛莎·涅尔著:《逻辑学的发展》,商务印书馆1985年版,第166页。
② 周礼全等译,塔尔斯基著:《逻辑与演绎科学方法论》,商务印书馆1989年版,第24页。
③ 金岳霖:《逻辑》,生活读书新知三联书店1961年版,第137页。
④ 罗素:《数理哲学导论》,商务印书馆1982年版,第137页。
⑤ Whitehead and Russell,Principiao Mathematica,Vol.I.,second edition,Cambridge,1925,p.94。
⑥⑨(12)(13)(278)(29)(32)(33)(34) 李国山编:《刘易斯文选》,社会科学文献出版社2007年版,第209,5,11,6,100,8,7,10,13页。
⑦⑧(20) Daniel J.Bronstein,The Meaning of Implication,Mind,New Series,Vol.45,No.178(Apr.,1936),p.159,161,162。
⑩(11)(15) C.I.Lewis,Implication and the Algebra of Logic,Mind,New Series,Vol.21,No.84(Oct.,1912),p.522,522,522。
(14)(31) C.I.Lewis,The Calculusof Strict Implication,Mind,New Series,Vol.23,No.90(Apr.,1914),p.247,241。
(16)(17)(18)(19)(21)(22)(23)(24)(25)(27) C.I.Lewis and C.H.Langford.Symbolic Logic,The Century Co.p.153,153,124,124,124,154,174,175,247,250-251。
(26) C.I.Lewis,survey of symbolic logic,1918.p.338。
(30) Ian Hacking,what is strict Implication?The Journal of Symbolic Logic,Volume 28,Number 1,March 1963:51。
【责任编辑:赵小华】
B81-06
A
1000-5455(2010)06-0094-05
2009-09-22
教育部人文社会科学研究一般基金项目“模态逻辑和美国实用主义哲学研究”(08JA720010)
杨福荣(1975—),男,陕西富平人,华南师范大学政治与行政学院博士研究生,宝鸡文理学院政法系讲师;周祯祥(1949—),男,湖北武汉人,华南师范大学政治与行政学院教授、博士生导师。
