基于最优线性拟合的WSN时间同步算法研究*

吴宝明,李声飞

1.第三军医大学大坪医院野战外科研究所,创伤烧伤与复合伤国家重点实验室,重庆 400042;2.重庆大学通信工程学院,重庆 400040

时间同步是无线传感器网络的重要支撑技术,很多传感器网络的应用和算法都需要统一的时钟基准,如数据融合、节点定位、休眠周期的同步、TDMA定时等[1]。所以研究一种高效、精准的时间同步算法具有重要的科研意义和实用价值。目前常用的无线传感器网络时间同步算法有：RBS算法[2]、TPSN算法[3]、DMTS算法[4]和 FTSP算法[5-6]等。其中RBS算法是基于单向广播机制,它排除了发送端对同步精度的影响,达到了较高的同步精度,但其计算量和同步开销较大,能耗较高;TPSN算法基于双向成对同步机制,同步效果较好(RBS同步精度的两倍[3]),但能耗也较大,算法鲁棒性较低;而 FTSP算法结合单向广播机制和双向成对机制,采用 MAC层打时间戳和线性回归补偿时间漂移和偏移的方式,达到了较高的同步精度,更适用于资源受限的传感器网络时间同步。但算法收敛时间较长,易受异常数据点影响[7],且对密度大的多跳网络,泛洪广播发送数据包容易引起数据碰撞。

通过对以上时间同步算法比较和总结,笔者选取 FTSP算法实现时间同步。在分析 FTSP算法基础上,针对其缺点在同步开销和异常数据处理方面予以改进,提出了基于最优线性拟合的时间同步算法。该算法采用节点分级策略而减少同步所需信息包开销,并通过分析影响时间同步的因素,提出了基于参数估计的回归算法,消除异常数据点对回归曲线的影响,提高了同步精度。

1 FTSP同步算法介绍

FTSP算法由 Vanderbilt大学的 Branislav Kusy等[5-6]提出的,是基于发送者-接收者的同步算法。它结合单向广播和双向同步算法的优点,采用泛洪层次结构广播同步报文,减少了同步信息开销,对网络拓扑结构变化和根节点失效有较好的健壮性。通过 MAC层打时间戳方法,缩短了消息传输延迟的不确定性,使同步精度达到 μs级。

FTSP算法采用一元线性回归来估计节点时间漂移率和偏移,并对其进行补偿[7]。节点收到同步消息数据包 SYNC后,构造本地时间-全局时间数据对,经过 N次信息交换,构造回归表((t1,T1),(t2,T2),…(tn,Tn))。将回归表中数据代入公式(2)和(3)估算时间漂移率和时间偏移

式(1)为本地时间与全局时间关系。式(2)、式(3)中,Ti、ti分别为第 i次同步周期的全局时间和本地时间 ,为全局时间和本地时间的期望 ;通过计算时间漂移率和偏移后,在每秒的末尾对节点本地时间进行补偿。而考虑到一定时间范围内节点晶振频率是稳定的[8],则本地时间与全局时间成线性关系。通过构造最佳拟合曲线 L,在误差允许的范围内,可以通过 L直接计算某一时刻本地时间与全局时间偏移,从而减少了同步消息的发送次数,降低了节点能量消耗[9]。

2 基于最优线性拟合的时间同步算法

FTSP算法采用 MAC层时间戳和线性回归补偿时间偏移和漂移,降低传输延时的不确定性,具有较高的同步精度。但它也存在一些问题：(1)对于密度大的多跳网络,采用泛洪广播发送同步包,容易引起网内数据碰撞,导致同步包中只有一小部分会被利用,大部分同步包被当做冗余数据包而被抛弃,这样非常消耗能量和网络资源;(2)线性回归算法易受到异常数据点影响,拟合出的回归曲线不仅不会提高同步精度,反而引入更大的误差,造成不必要的计算。

针对以上问题,笔者对传统的 FTSP算法进行改进,设计一种新的消息包传输机制,通过将节点分为主动节点和被动节点方式,减少同步所需的通信开销;对线性回归算法进行改进,引入概率统计论中的参数估计理论,对进入同步表中的数据对进行可信度判断,消除误差较大的数据对拟合曲线的影响,达到了精确的时间同步,同时也延长了节点同步时间,进一步节省了节点的能耗。具体实现过程如下。

2.1 分级消息包传输机制

针对上述 FTSP算法存在的问题(1),笔者设计一个低开销的数据包传输机制：将消息包传输过程分为节点分级、统计节点度和主/被动节点选择三个阶段

(1)节点分级

假设网络中节点通信距离有限,通过广播消息包的形式实现分级。根节点选定后,设定它的级别为 0级。根节点广播信息包(包含节点级别和当前时间戳),周围节点接收到信息包后,利用同步算法实现时间同步,并提取信息包中节点级别加 1做为本节点的级别,这样以此类推,依此实现网络节点分级。

(2)统计节点度

分级完成后,开始统计各节点的下级节点度,即节点广播范围内下级节点的个数。在一个同步周期内,若i级节点收到一个i+1级节点发送的同步包,则它的下级节点度加一,依此类推统计每一级节点的下级节点度。

(3)主动 /被动节点选择

完成以上两步后,进行主/被动节点选择。方法如下：若节点的下级节点度为 0,将其设置为被动节点;若节点达到同步且下级节点度不为 0时,通过比较同级节点中下级节点度最大的节点,做为该级的主动节点,其它节点做为被动节点。

这样经过几个同步周期,网内各级中只有下级节点度最大的节点为主动节点,发送同步信息包,其它节点都为被动节点,这样大大的减少了时间同步开销,节省了节点能耗。

2.2 参数估计的线性回归算法

针对上述 FTSP算法存在的问题(2),FTSP算法中未采取有效措施来消除这种影响[6]。笔者采用概率统计论中参数估计理论[10],设置置信区间来判断进入回归表中数据对的合法性。选取同步包中的全局时间 T和回归表已有的数据对,来预测本地时间 t的范围,具体方法如下：

设 t0是节点收到全局时间 T0时对应的本地时间,依据前式,t0的预测符合：

上式(5)是典型的一元线性回归模型[10](给定的 x的一定的置信度区间,可以预测出 y的取值范围),其中为回归系数,以下采用参数估计的最小二乘法[10]来估计以上未知量。ε服从正态分布,由式(5)知,则服从如下正态分布：

其中 STT为全局时间 T的 2阶中心距并能够证明 t与相互独立[10],由式 (4)、式(6)得。

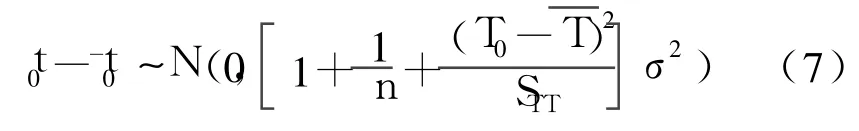
又由本地时间 t的残差平方和为：

Qe称为残差平方和,是 σ2的无偏估计

由式(9)可知,残差平方和与 σ2的商服从分布卡方分布[10]：

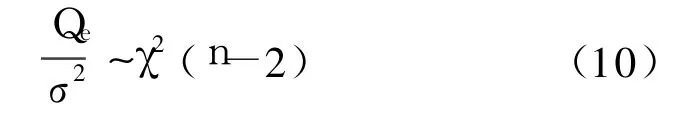
将式(9)代入上式有：

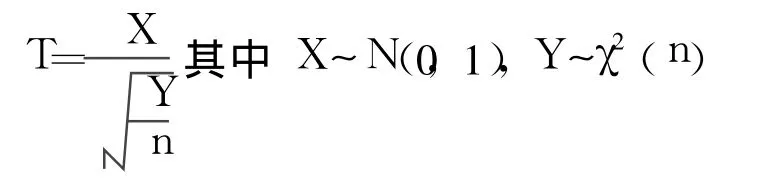
可得到 t0服从的 t分布为：

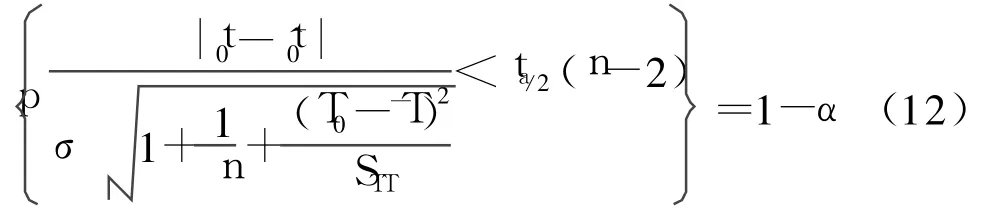
于是对于给定的置信度区间 1-α,有

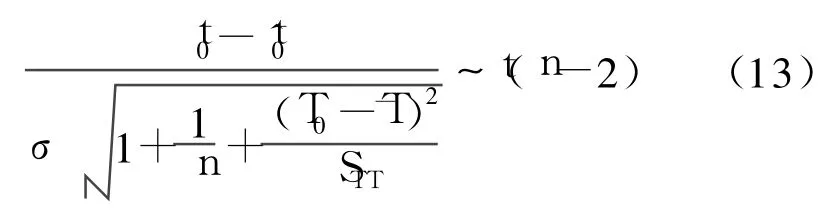
则可得 t0的预测区间[10]为：

称为 t0的置信度为 1-α的预测区间。

若回归表中数据点比较多,式(14)中的根式近似等于 1,若选择 t0的置信度为 0.99时,查表知为 2.896,则 t的预测区间近似为：

从式(15)可以看出,本地时间的预测区间计算量比较大。由于是 σ2无偏估计,则有可用 σ来近似代替σ2为误差分布的方差,这个误差是由消息包传输延迟引入的,可以通过分析节点的时延分布特性来估计这个值(笔者针对本节点硬件特性,通过大量测试误差为27.7μs)。在一次同步过程中,得到本地—全局数据点(ti,Ti)。根据全局时钟 T和回归表已有的数据,估计出 t的预测区间,并判断当前本地时间 t是否在预测区间内。若在预测区间内,则说明这个数据是可信的,将其加入线性回归表;若不在区间内,则表示这是异常数据将其抛弃,不需要更新线性回归表。

采用以上预测区间,虽然增加了计算复杂度,但避免了异常数据对回归曲线的影响。如果进一步增大置信度,将得到限定更加严格的可信区间,选出最优数据进行估计。

3 仿真结果分析

3.1 实验建立

本文采用自行研制的传感器节点搭建实验平台。节点的处理器采用 TI的 CC2430射频芯片,它是一个内嵌增强型 C8051的无线射频收发模块,支持算法在 MAC层打时间戳。节点外部有两个晶振：32.768 kHz和 32 MHz,选取 32 MHz石英晶振做为节点的振荡时钟源。实验平台由 5个节点(编号为 node1～node5)组成,其中一个节点做中心节点,其它节点均为网络中处于不同层次的子节点(节点距离为 10m),组建一个 level为 2的时间同步系统,进行单跳时间同步测试。测试平台示意图如图 1所示,测试方法如下(所有节点最小定时单位为 10μs)。

图1 时间同步测试图

(1)中心节点(node1)建立网络并定时 1 s周期性的广播时间同步信息包,3个子节点(node2～node4)加入网络后接收同步包,并利用本文提出的算法修改本地时间与中心节点保持同步;

(2)将节点配置为每次激励信号电平跳变就报告本地时间到 PC机。采用定时器(文中选取 time3的 0通道)捕获 IO口输入电平跳变(上升沿),在捕获中断中,通过串口报告节点本地时间到 PC机。

(3)采用函数发生器产生标准方波(文中选择周期为 100 ms,占空比为 50%的方波)做为激励事件,接到节点上具有捕获能力的 IO口上;值得注意的是,公共的脉冲方波信号不能有额外的杂波,才能保证每次查询都在同一时刻进行。

3.2 同步精度稳定性试验及分析

为了查看网络中各节点时间同步精度,笔者任意选取一节点(以 node4为例),查看它的本地时间与中心节点(node1)的时间偏差。随机选取开始查询时间,查询次数为 20次(约为 2 s),每次间隔为100ms,PC机串口接收的时间数据如图 2所示。

图2 Node4时间同步比较图

由图 2可知,以 node4为例,开始查询时刻为0x00 15 08 00 C8 54,即在全局时间为 15 min 8 s 200(0x00C8)ms 84μs时,查看 node4节点本地时钟与全局时钟的误差。可见 20次同步误差范围在-10 μs～40 μs间,平均误差为 2.35 μs,Node4能够很好的与中心节点保持时间同步,同步精度在μs级。

为了进一步查看子节点与根节点(node1)的同步情况,笔者任选两节点(node2和 node4),随机选取从开始查询时刻(node2比 node4晚),连续查询150次同步事件,查询间为隔 100 ms,总测试时间约为 15 s。得到两节点的同步误差曲线如图 3所示(最小定时单位为 10μs)。

图3 同步误差曲线

图3(a)(b)知,node2的误差在 -50μs～90μs之间,均值为 1.286 7μs,方差为 8.044 8;node4的误差在 -90μs～80μs之间,均值为 0.42 μs,方差为 13.856。node4的误差波动范围明显要比 node2波动范围要大(node4方差比 node2大),分析其原因知 node4的开始查询时间比 node2要早(相差15min),线性回归算法未拟合出最佳估计曲线,随着时间增长,同步误差会逐渐趋于稳定。两节点的误差范围都在 μs级,误差呈正负交错波动,且有逐渐减小的趋势,可见算法收敛性较好,能够有效的减少同步误差。可得到以下结论：以上两节点能够很好的与中心节点保持同步。

为了比较本文的算法与 FTSP算法同步精度差异,任选 1个节点(笔者选取 node2),分别采用本文的算法和 FTSP算法实现该节点与中心节点(node1)时间同步,比较两算法的同步误差曲线如图 4所示。查询次数为 200次,查询间隔为500m s,总测试时间约为 100 s。

图4 两种同步算法误差对比图

从图 4中可以看出：同步精度方面,FTSP的同步误差在 -40μs～400μs间,且误差与同步周期有密切关系,随着同步周期增加误差逐渐增大,在每一个周期内,误差随时间线性增大,级间误差会发生陡变情况。分析知主要有以下两点原因：(1)节点晶振存在频率漂移,随着同步周期变大,漂移产生的误差累计而带来了更大的误差;(2)异常数据点进入回归表,导致线性拟合曲线计算出的全局时间与真实值偏差很大,导致个别同步周期的同步误差很大。

相比之下本文提出的同步算法,误差范围控制在 -90μs～40μs内,远远小于前者,且在 100 s(200次查询时间)时间内能够维持较高同步精度。而误差波动也较为稳定,不会随着同步周期的增加而陡变的情况。这是由于改进的算法采取补偿晶振时间漂移方式,防止误差随周期增长而累加,并采取有效措施避免异常数据点对同步精度影响,从而获得了更加平稳的误差曲线,算法收敛时间缩短。可见采用本算法后,算法的执行周期显著增大,适合于资源受限的无线传感器网络的应用。

由于无线传感器网络对不同的应用环境中表现出不同特点,对时间同步要求也存在差异。所以在分析同步算法时,一般在同步方式,误差,通信开销,能耗和有效范围方面进行比较,笔者对 RBS、TPSN和本文算法在以上方面进行对比,如表 1所示。

表1 三种同步算法比较图

表中 RBS和 TPSN算法数据是参考文献[11]在 Mica平台上获取的,通过比较可看出本算法同步精度介入 TPSN算法和 RBS算法之间,达到了较高的同步精度,能满足一般传感器网络应用需求;在运算复杂度和能耗方面都优于其它两种算法;在同步开销方面,受到技术限制只限于理论上分析,传统的FTSP算法一次同步周期需要 o(n2)个信息包开销,而本文算法仅需要 m◦n(m为级数,n为当前级活动节点数)个信息包开销,减小了同步通信开销,降低节点能耗和计算量,减轻了节点的负担。因此本算法更适合于能量、资源受限的传感器网络应用。

4 结论

目前针对资源、能量受限的传感器网络时间同步算法研究相对较少,很多算法仍处于仿真阶段,与实际应用有一定距离。本文在分析 FTSP算法基础上,主要在同步开销和异常数据处理方面对其进行改进。采用节点分级策略,较少了同步通信开销;采用概率统计理论中参数估计思想,排除了异常数据点的影响,提高了回归曲线的跟踪精度。最后通过实验测试表明：本算法在保证精度的前提下,大幅度提高算法的执行周期,减少了同步通信开销,在各方面优于传统的 FTSP算法,更适用于能量受限的无线传感器网络的应用。

[1]周中良,于雷,潘泉.综合化多传感器空间管理模型与算法研究[J].传感器技术学报,2007,20(11)：256-259.

[2]Elson Jeremy,Girod Lewis,Estrin Deborah.Fine-Grained Network Time Synchronization Using Reference Broadcasts[C]//Proceedings of the Fifth Symposium on Operating Systems Design and Implementation.Boston,MA,2002：147-163.

[3]田贤忠,陈登,胡同森.无线传感器网络按需时间同步算法研究[J].传感器技术学报,2008,21(11)：1881-1886.

[4]张杰,石为人.基于无线传感器网络的信息采集检测系统设计[J].传感技术学报,2009,22(6)：861-864.

[5]Philipp Sommer,Philipp Sommer.Gradient Clock Synchronization in Wireless Sensor Networks[J].2009：37-48.

[6]Kyoung-lae Noh,Serpedin.A New Approach for Time Synchronization in Wireless Sensor Networks：Pairwise Broadcast Synchronization[J].Wireless Communications,2008,9,7(9)：3318-3322.

[7]周贤伟,韦炜.无线传感器网络的时间同步算法研究[J].传感技术学报,2006,19(1)：20-25.

[8]黄天戍,陈苒菁.石英晶振频率测试系统的研究与开发[J].中国仪器仪表,2005,(10).

[9]孙利民,李建中,陈渝,等.无线传感器网络[M].北京：清华大学出版社,2005：158-176.

[10]杨虎,孙琼荪,钟波.数理统计[M].北京：高等教育出版社,2004：103-135.

[11]Ganeriwal Saurahh,Kumar Ram,Srivastava Mani.Tim ing Sync Protocol for Sensor Networks[C]//ACM SenSys.Los Angeles,CA,2008.