无线传感器网络线性调频扩频测距方法研究*

杨清玉,于 宁,王 霄,冯仁剑

(北京航空航天大学仪器科学与光电工程学院,北京 100191)

传感器节点自定位是无线传感器网络(wireless sensor network,WSN)的关键技术之一,基于距离的定位算法比与距离无关的定位算法精度高[1]。在基于距离的定位中,测距采用的方法有测量信号的到达时间(Time of Arrival,TOA)、到达时间差(Time Difference of Arrival,TDOA)、接受信号强度指示(Received Signal Strength Indicator,RSSI)和到达角度(Angle of Arrival,AOA)等[2-3]。用于测距的信号主要有超声波、激光、红外线、电磁波等。WSN节点通常利用超声波进行测距。由于超声波容易受到环境温度、风速、触发时间、硬件响应时间的影响,导致测距性能不太稳定。室内多径效应的影响限制了它的传播范围,测距范围一般小于 10 m[4-5]。

对于室内无线信道,多径成分相当丰富,不同路径到达接收机的时间和相位的特点会给信号测量带来不同影响。如果各径到达相位相同,则影响是有益的,求和后的效果是能量增加;如果各径到达相位不同,则影响是有害的,接收机接收到的信号能量会急剧衰落。很明显,前者发生的概率很小,多径效应一般会给室内通信带来严重的衰落[5]。因此,亟需探寻一种新型测距方法,满足传感器节点在复杂室内通信环境下的定位需求。采用 Chirp信号代替超声波,以避免室内多径效应的影响,具有发射功率低、通信稳定性好、抗干扰能力强等优点。

1 Chirp信号理论

Chirp信号是一种扩频信号,具有很强的自相关和自同步特性,在一个信号周期内表现出线性调频的特性,可由声表面波滤波器产生[7]。线性调频扩频(Chirp Spread Spectrum,CSS)技术来源于雷达系统中以 Chirp信号为核心的脉冲压缩理论[8],经过脉冲压缩输出的信号具有 Sinc函数包络[9],工作于2.4GHz频段,由于 Chirp信号扩展带宽 80MHz,平衡了多径效应中的能量增加和衰落,避免了多径效应的影响[10-11]。

Chirp信号的数学表达式为：

式中,t是时间,s(t)是 Chirp信号,a(t)是包络,f0是中心频率,μ是扫频率(Hz/s)。当 μ取正时,信号为 Up-Chirp,当 μ取负时,信号为 Down-Chirp,T是信号周期。Chirp信号是 MDMA(Multi Dimensional Multiple Access)方式的成功应用,融合了 AM(Amplitude Modulation)、FM(Frequency Modulation)和 PM(Phase Modulation)三种调制[11],其时域、频域图如图 1所示。

图1 Chirp信号时域、频域图

如果 a(t)是矩形函数,通过对应的匹配滤波器后,其输出为：

CSS接收数据时利用了脉冲压缩原理,匹配滤波可以在很短的时间内获得很大的能量,接收机通过对能量的捕获能够把数据符号提取出来。

可以通过频率交叠技术(使用一系列重叠的Chirp信号),提高传输速率而不需要改变 Chirp信号的其他性质。用交叠系数 Of表示交叠程度：

式中,TS为信号间隔,Of＜1表示 Chirp信号没有交叠的成分;Of＞1表示在 T内有 Of个 Chirp信号交叠,速率为单一 Chirp信号的 Of倍[12]。

2 基于CSS的测距方案

基于CSS的测距过程如图 2所示。

图2 基于CSS的测距过程

该测距过程包括两次对称测量和一次距离修正。

第一次测量由节点 1向节点 2发送数据包,并接收来自节点 2的自动应答,节点 1计算出从发出数据包到接收应答的传播延迟 T1,节点 2在接收到节点 1的数据包时开始计时,并在返回应答后停止计时,得到节点 2的处理延迟 T2。第二次测量由节点 2向节点 1发送包含 T2有效信息的数据包,并接收节点 1的自动应答,同理,节点 2计算出传播延迟 T3,节点 1计算出自己的处理延迟 T4。最后,节点2向节点 1发送包含 T3有效信息的数据包。节点 1根据已知信号传播速度和获得的 4个延迟时间由公式

计算出两节点间距离 d,其中 c为射频的传播速度,约为光速。

在接收数据时利用了脉冲压缩原理,一定程度上可以看作是求自相关。由于 Chirp信号的扩频和很强的自相关特性,在求自相关提取信号时,具有很好的抗干扰能力,消除了多径效应的影响和降低了噪声干扰。

T1、T2、T3、T4的测量偏差分别为 δT1、δT2、δT3、δT4,由于 T1、T4由节点 1的晶体振荡器测得,令其测量偏差均为 δ1,T2、T3由节点 2的晶体振荡器测得,令其测量偏差均为 δ2,距离偏差 δd可由公式(5)求得。

计算结果表明该方法消除了因为时钟漂移导致的误差。

为了提高测距精度,将测量距离与实际距离进行最小二乘拟合。模型建立如下：假设给定点(di,dm)(i=0,1,…,m),d为测量距离,dm为拟合距离,ak为拟合系数,Φ为所有次数不超过 n(n≤m)的多项式构成的函数类,现求

使得残差平方和

当 n=1时,称为线性拟合或直线拟合。显然 I为a0,a1,…an的多元函数,上述问题即为求 I=I(a0,a1,…an)的极值问题。由多元函数求极值的必要条件,得

即

式(9)是关于 a0,a1,…an的线性方程组,可解出 ak(k=0,1,…,n)。

3 测距方案实现

3.1 实验环境与操作

室内环境选取大楼内走廊,走廊的平面示意图如图 3所示,其主要特征为：

①空间狭长,没有阻挡物;

②一侧墙壁上有四扇玻璃窗(宽 1.7 m,高2.3m),窗外有铁楼梯,另一侧开有多扇木门。

图3 走廊平面示意图

无线传感器网络节点的射频部分采用 NA5TR1芯片产生 Chirp信号,射频部分通过 SPI和处理器进行数据传输。定位节点通过串口和 PC机相连,上传测量结果。考虑到走廊的实际长度,测距范围从3m到 42m,每隔 3m有一个测距点,每个测距点测量 3 000次,去除最大值和最小值各 50个,取平均值为该点的测量值。

3.2 软件设计

测距节点包含两类：定位节点和信标节点,应用程序需分别设计,测距程序流程如图 4所示。

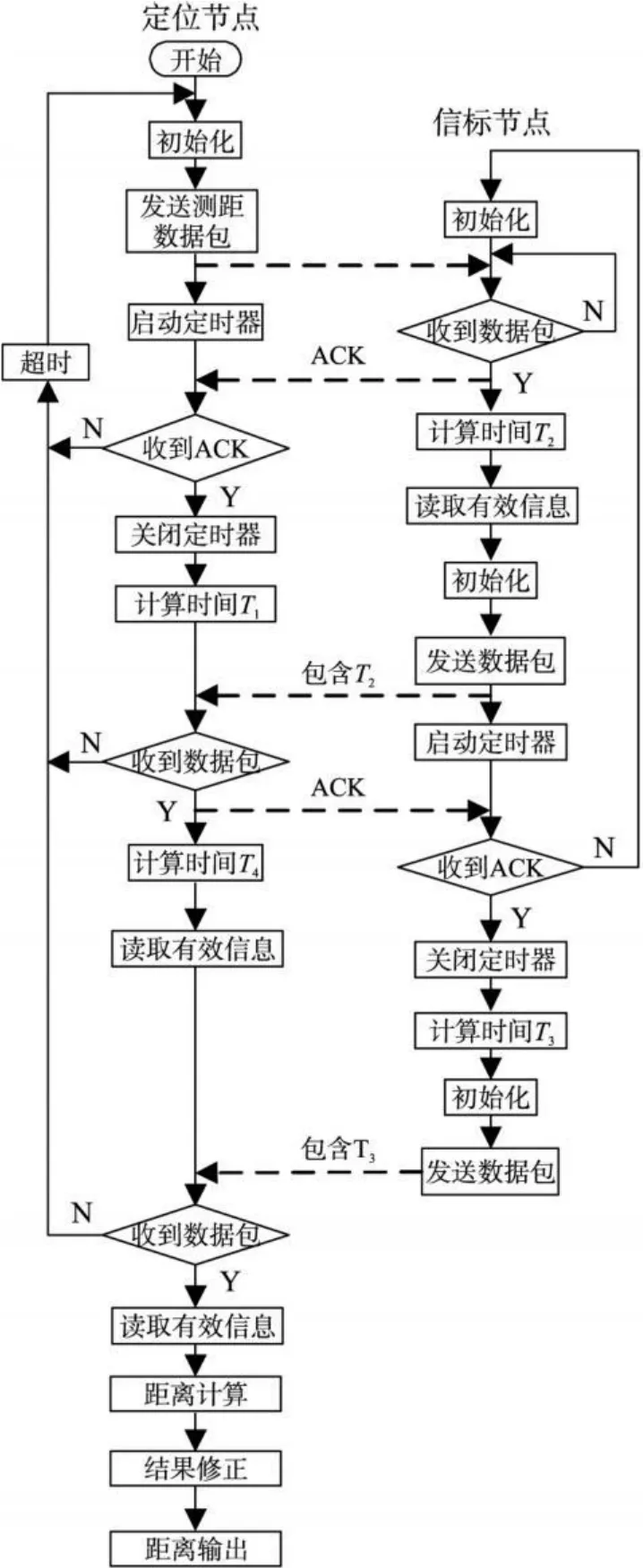
图4 信标节点/定位节点测距程序流程图

定位节点向信标节点发送测距数据包,当信标节点收到数据包时,自动回复 ACK(Acknowledgement),计算处理延迟,定位节点根据接收到的信标节点的 ACK计算出信号传播延迟,如果定位节点没有收到 ACK或接收超时,就会重新初始化下一次测距过程。信标节点向定位节点发送数据包(包含上一次的处理延迟),根据接收到定位节点的 ACK计算出此次信号的传播延迟,定位节点计算此次处理延迟。信标节点再将包含传播延迟的数据包发送给定位节点。定位节点根据四个时间值,调用距离计算函数,计算出两节点间的距离,利用距离修正公式修正结果,存储修正后的距离值,并通过串口输出。

4 实验结果与分析

实验结果如图 5和图 6所示。

图5为实际距离、测量距离和修正距离三者之间的关系图。从图 6可看出,当距离增大到5 m后,误差变化趋势减缓。

为了进一步减小测量误差,利用最小二乘原理对基于CSS的测距实验结果进行线性拟合,得到测量距离 d与拟合距离 dm的关系为：

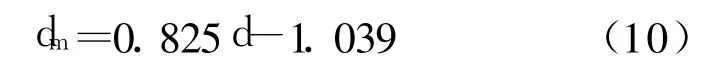
其剩余标准偏差为 2.556。

由于线性拟合的计算简单且其结果能够满足测距要求,本测距方案只采用线性拟合对测量结果进行修正。

图7为相同实验环境下,基于CSS测距与基于超声波的 TDOA测距的对比图,当距离大于 9m时,超声波测得距离无穷大,无法实现测距。由图 7可知,基于CSS的测距范围大,小距离测量精度不如超声波测距,在实际无线传感器网络节点的测距中,可根据测距结果,采用相应测距方案,如首先采用CSS测距,若测距结果小于某个预设值,改用超声波的 TDOA测距,以提高整体测量精度。

图7 基于CSS测距与基于超声波的TDOA测距对比图

5 结论

CSS测距技术通过对 Chirp信号进行脉冲压缩处理,具有发射功率低和抗干扰能力强的优点,避免了多径效应的影响,能够满足传感器节点在室内复杂通信环境中的定位需求。虽然该技术在小距离测量方面精度略低于基于超声波的 TDOA技术,但随着距离的增大,其相对测距误差逐渐变小。CSS技术较大的测距范围使其更适合室内远距离测量。文章在实验数据统计规律基础上建立的最小二乘线性拟合距离修正模型可以有效提高CSS的测距精度。

[1]Zhu Yanping,Huang Daqing.Localization Algorithm Using Distance and Angle Information in Wireless Sensor Networks[J].Transactions of Nanjing University of Aeronautics＆Astronautics,2009,26(1)：58-63.

[2]Patwari N,Ash JN,Kyperountas S,et al.Locating the Nodes：Cooperative Localization in Wireless Sensor Networks[J].IEEE Signal Processing Magazine,2005,22(4)：54-69.

[3]Sayed A H,Tarighat A,Khajehnouri N.Network-Based Wireless Location：Challenges Faced in Developing Techniques for Accurate Wireless Location Information[J].IEEE Signal Processing Magazine,2005,22(4)：24-40.

[4]蒋林,闫继宏,臧希喆,等.一种新的超声波绝对定位方法[J].吉林大学学报,2009,39(1)：188-193.

[5]王文生,齐广学,温淑慧,等.一种高精度超声测距方法的研究[J].传感技术学报,2002,9(3)：219-221.

[6]Hashemi H.The Indoor Radio Propagation Channel[J].Proceedings of the IEEE,1993,81(7)：943-968.

[7]Bush H,Martin A,Cobb R,etal.Application of Chirp SWD for Spread Spectrum Communications[C]//Proc.of the IEEE Ultrasonics Symposium,1973：494-497.

[8]Morgan D P.Surface-Wave Devices for Signal Process-Ing[M].Amsterdam,Elsevier Science Publishers B.V,1985：214-219.

[9]赵敏,吴卫山.线性调频信号特性分析[J].航空兵器,2009(1)：25-29.

[10]IEEE Computer Society,IEEE Std 802.15.4a-2007[S].Aug.2007.

[11]Nanotron Technologies GmbH.Nano NET Chirp Based Wireless Networks,White Paper,V 1.04[EB/OL].http：//nanotron.com/EN/pdf/WP_CSS.pdf.

[12]张鹏.基于Chirp的宽带超宽带通信技术研究[D].成都：电子科技大学,2007：23-31.