考虑不确定性因素的多学科设计优化方法
2010-05-05李元生敖良波温志勋岳珠峰
贺 谦 李元生 敖良波 温志勋 岳珠峰
(西北工业大学工程力学系,西安,710129,中国)
INTRODUCTION
Multidisciplinary design optimization(MDO)considering coupled systems is well-suited for complex engineering structure design and is widely used in many industrial domains,such as aeronautics,astronautics,and automobile.Conventional MDO is deterministic without considering inherent uncertainties which exist in design parameter, materialproperty and mathematical modeling of an actual engineering system.Deterministic optimization without considering variability is unreliable,which can lead to catastrophic failure.Therefore,the reliability-based multidisciplinary design optimization(RBMDO)should be considered to overcome the drawback of deterministic MDO.
In the last few years,the field of reliabilitybased design optimization(RBDO)has caused increasing research attention.A variety of different approaches for RBDO have been proposed,which can be divided into three broad categories.The first category consists of approaches in which the RBDO problem is formulated as a double-loop(DL)optimization problem[1-2].The approach is a nested optimization process with expensive calculation and is not suit for a complex structure.In the second category,referred to as the decoupledmethod(DM)[3-5],the reliability analysis and the optimization are decoupled.So DM is more efficient than DL.However,DM requires an iterative process to analyze the reliability and is impractical for artifacts with a large number of failure mechanisms.The third category process,the RBDO problem with a single-loop (SL)method[6-7],which can significantly reduce computational cost because there is no iteration during the reliability analysis.The category is practical for complex engineering systems.In this pa-per,an effective RBMDO framework is proposed by integrating MDO with SL method.
1 MDO METHOD
There are five MDO architectures[8]in the current phase,including multidisciplinary feasible(MDF),individual discipline feasible(IDF),collaborative optimization (CO),concurrent subspace optimization(CSSO),and bi-level integrated system synthesis(BLISS)methods.MDF is a commonly used MDO framework[9-10]which includes an optimizer and a multidisciplinary analysis(MDA)process.For MDF,all discipline design variables are treated as the global variables and all discipline objectives are system objectives for the optimization.MDF can be described as follows
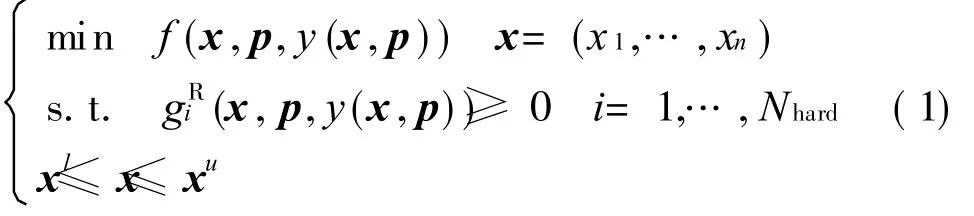
where x is the vector of design variables,p the vector of fixed parameters,y the state variables,the i th constraint that models the ith critical failure mechanism of the system. The design space is bounded by xland xu.
The computational cost of MDF is high for the complex structure because of MDA iteration.In order to improve the efficiency,a Kriging approximate model is used to replace MDA during the optimization.
A Kriging model is a combination of a polynomial model plus departures in the form of
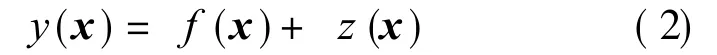
where y(x)is the unknown function of interest,f(x)the unknown function of x,and z(x)the realization of a stochastic process with mean zero,variance e2and non-zero covariance.The f(x)term in Eq.(2)provides a"global"model of the design space andis similar to the polynomial model in a response surface.For more details on the Kriging model,please see Ref.[11].
To set up a Kriging approximate model,a database composed of several sample points is needed,and the database can be built up by the design of experiment(DOE)technique.In DOE,a design matrix is constructed in a systematic fashion that specifies the values for the design parameters of each sample point,or the experiment. A number of experimental design techniques exist for efficiently sampling values of design parameters,such as the central composite design,orthogonal arrays and the Latin hypercube. For more details on experimental design techniques,please see Ref.[12].
A Kriging model based MDF process includes five steps: (1)Selecting a set of design points,taking MDA at each point and building up database,which can be implemented by DOE;(2)Setting up the Kriging approximate model based on the database;(3)Utilizing the Kriging model to search the approximate best solution in design space;(4)Analyzing the best design by MDA process; (5)Adding MDA results to database and updating the Kriging model. Repeating steps(3—5)until the convergence is achieved.
2 SL-BASED RELIABILITY ANALYSIS
Conventional reliability analysis methods include the first-order second-moment(FOSM),the advanced first-order second-moment(AFOSM),and the second-order second-moment(SOSM)approximation techniques.These methods need iterative processes to analyze the reliability and are not efficient during RBMDO for complex engineering.Compared with the methods mentioned above,SL is more efficient on reliability analysis because it avoids the iterative process for calculating the most probable points(MPPs)of the failure,which suit well with the reliability analysis of complex structures.
Besides,x1,x2,…,xnare a set of random variables and each random variable is assumed as the non-normal distribution(almost all random variables are non-normal distributions in complex engineering systems). The meritfunction is shown as Z=gx(x1,x2,…,xn)and the limit state equation is expressed as Z=gx(x1,x2,…,xn)=0.The SL-based reliability analysis (SLBRA)method includes transforming non-normal random variables to standardized normal variables,setting up an equation between M PP and the mean of random variables,substituting reliability index(U)into the equation and calculating M PP.The main steps of SLBRA are as follows:
Step 1 Giving the initial values of random variables(xi),the mean values of xi(_i)are commonly used;
Step 2 Transforming non-normal variables to standardized normal variables using the following formula
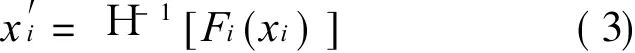
where Fi(xi)is the marginal cumulative distribution function of non-normal distribution,H-1[· ]the inverse function of the standard standardized normal distribution function;
Step 3 Calculating the mean valuesand standard variances of normal variables from Step 2 according to Eqs.(3,4)

whereh[· ]is the density function of the standard standardized normal distribution,and fi(xi)the density function of non-normal distribution;
Step 4 Based on Eq.(3),the MPP coordinatesin standard normal space can be expressed by the MPP coordinatesin non-normal space as Eq.(6).′is calculated by Eq.(7).Substituting Eq.(6)into Eq.(7),Eq.(7)can be rewritten as Eq.(8).From Eq.(8),the relationship betweenand xican be given as Eq.(9)according to the Rackwitz-Fiessler method
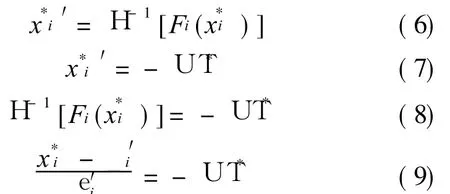
whereT*is the vector of the direction cosines of Uat
Step 5 Calculating T*based on Eq.(10)
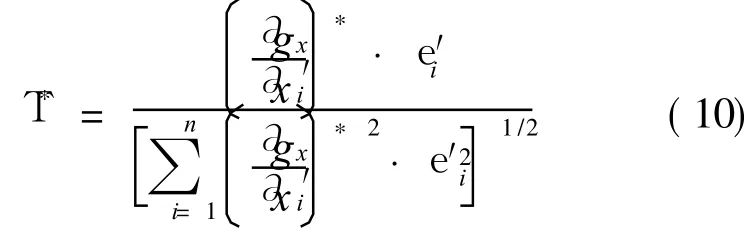
Step 6 Substituting the required reliability index Ureqdinto Eq.(9),the relationship between x*iand_′ican be given as
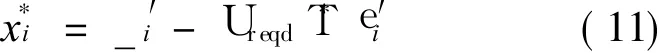
The limit state equation can be expressed as gx)= 0 after six steps mentioned above,and the equation is the constraint during RBMDO.
3 SL-MDF RBMDO METHOD
A SL-MDF RBMDO method is proposed based on SLBRA and MDF,the method is described as follows
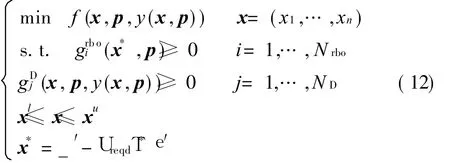
where x is the vector of random design variables,p the vector of fixed parameters,x*the MPPs,the reliability constraint function,and gDjthe deterministic constraint function. The random variable limits are xland xu.
The proposed method is efficient for complex engineering systems because it avoids iterative process in SLBRA.It involves:(1)determining design variables and building up database by DOE,setting up a Kriging approximate model;(2)finding M PP by SLBRA;(3)setting up reliability constraints at M PP gx(x*1,x*2,…,x*n)=0;(4)finding the optimal design as the mean values of random variables based on Kriging model;(5)MDA at the results from Step(4)and updating Kriging model.Steps(4—5)are repeated until the convergence is achieved.The whole process is shown in Fig.1.

Fig.1 Flowchart of SL-MDF RBMDO framework
4 APPLICATION EXAMPLE
A turbine blade optimization is taken as an example to verify the new SL-MDF RBMDO method.Firstly,the deterministic optimization is performed and the reliability of optimal results is analyzed to demonstrate the necessity of RBMDO.Then,SL-MDF RBMDO is implemented with the initial values achieved by deterministic optimization.The reliability analysis is also performed to verify the feasibility of the proposed method in an engineering system.Furthermore,the comparison between the proposed method and DL-based RBMDO method is performed to illustrate the efficiency of the proposed method.
Turbine blade optimization is a typical MDO problem which involves coupled analysis of several disciplines including aerodynamics,thermodynamics,structure,vibration,and life.In this paper,aerodynamics,thermodynamics and structure are considered for the sake of simplification.The coupled system of these disciplines is shown in Fig.2.
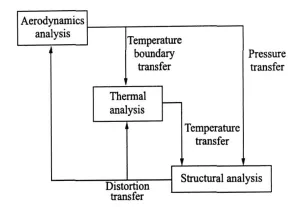
Fig.2 Aerodynamics,themodynamics and structure coupled system of turbine blade
The design variables defined by DOE include front radius,front constructional angle and airflow inlet angles of blade top section and blade bottom section,respectively. The definition of the design variables are shown in Fig.3,where design variables are defined in one blade section because the design variable names of both sections are same. The blade maximaltemperature(Tmax),the blade tip maximal transformation(Umax)and the blade maximal stress(emax)are constraint variables.The minimal total pressure loss(PLoss)is chosen as the objective variable.
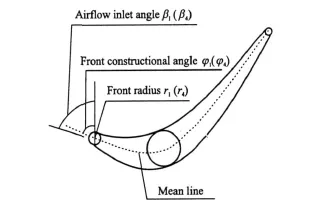
Fig.3 Definition of design variables
The deterministic MDO is performed by MDF and the reliability analysis is implemented by the Hasofer-Lind Rackwitz-Fiessler(HL-RF)method[13].The optimal and analytical results are shown in Tables 1,2.The safety probabilities of Umaxand Tmaxare acceptable because they reach 0.992 and 0.999 5,respectively.However,the reliability of emaxis only 0.431 and cannot satisfy the engineering requirement.It indicates that the deterministic optimal results can lead to structural failure.It is essential to investigate RBMDO in engineering system optimization.
The design variables of deterministic MDO are defined as random variables and each randomvariable follows the Weibull distribution.SLMDF RBMDO method is implemented with the initial values achieved by deterministic optimization and the required probability is 0.95(the relative Ureqdis 1.645).The RBMDO problem is expressed as follows

Table1 Design/random variables and optimization results

Table 2 Constraints/objective and optimization results

HL-RF method is also used to analyze the optimal results to verify the feasibility of the proposed method.
The results afterSL-MDF RBMDO are shown in Tables 1,2.The safety probability of emaxincreases to 0.953 and meets the reliability constraint.PLossdecreases 4.3% compared to the initial value,but it is higher than the deterministic MDO result as uncertainties are considered.It indicates that RBMDO can achieve a more compromising design by decreasing performance to meet reliability requirement and finally keep balance between operation risks and performance.The comparison of blade profile lines between results before and after SL-MDF RBMDO is shown in Fig.4,where the coordinate unit is mm.
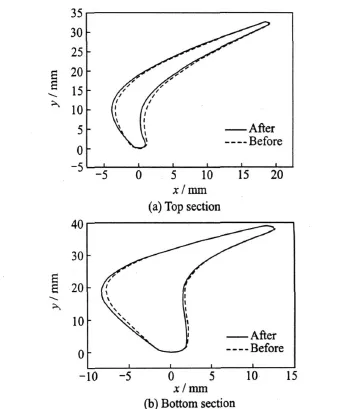
Fig.4 Comparison of profile lines between results before and after SL-MDF RBM DO
The DL-based RBMDO method is also implemented in turbine blade optimization with the same conditions to demonstrate the efficiency of the proposed method.The results are shown in Tables 1,2,which indicate that SL-MDF RBMDO method is much more efficient due to omitting iterations during the reliability analysis.
5 CONCLUSION
A new SL-MDF RBMDO framework is proposed by combining SLBRA method with MDF method.The Kriging approximate model is used and updated during the optimization process to reduce the computational cost of MDF.The proposed method decreases computational effort because it does not need iterative process during reliability analysis.A turbine blade design optimization is used to verify the proposed method.
The comparison of the optimal results between deterministic MDO and SL-MDF RBMDO indicates that RBMDO is necessary for engineering systemsand the feasibility ofthe proposed method.Compared with the commonly used DL-based RBMDO method,it shows that the proposed method is much more efficient and well-suit for complex engineering systems.
[1] Mahadevan S,Gantt C W.Probabilistic design optimization of a multidisciplinary system[R].AIAA-2000-4807,2000.
[2] Aminpour M A,Youngwon S U.A framework for reliability-based M DO of aerospace systems[R].AIAA-2002-1476,2002.
[3] Padmanabhan D,Batill S M.Decomposition strategies for reliability based optimization in multidisciplinary system design[R].AIAA-2002-5471,2002.
[4] Fan Hui,Li Weiji.An efficient method for reliability-based multidisciplinary design optimization[J].Chinese Journal of Aeronautics,2008,22:335-340.
[5] Agarwal H,Renaud J E.New decoupled framework for reliability-based design optimization[J].AIAA Journal,2006,44(7):1524-1531.
[6] Wang Liping,Kodiyalam S.An efficient method for probabilistic and robust design with non-normal distributions[R].AIAA-2002-1754,2002.
[7] Chen Xiaoguan,Hasselman T K,Neill D J.Reliability based structural design optimization for practical applications[R].AIAA-97-1403,1997.
[8] Yue Zhufeng,Li Lizhou,Yu Kuahai,et al.Multidisciplinary design optimization for aeroengine turbine blade[M].Beijing:Science Press,2007.(in Chinese)
[9] Perez R E,Liu H H T.Evaluation of multidisciplinary optimization approaches for aircraft conceptual design[R].AIAA-2004-4537,2004.
[10]Alexandrov N M,Lewis R M.Algorithmic perspectives on problem formulations in M DO[R].AIAA-2000-4719,2000.
[11]Han Yongzhi,Gao Hangshan,Li Lizhou,et al.Kriging model-based multidisciplinary design optimization for turbine blade[J].Journal of Aerospace Power,2007,22(7):1055-1059.(in Chinese)
[12]Schonlau M.Computer experiments and global optimization[D].Waterloo,Canada:University of Waterloo,1997.
[13]Rackwitz R,Fiessler B.Structural reliability under combined load sequences[J].Computers and Structures,1978,9:489-494.
