17号锻造钩尾框裂纹萌生寿命计算
2010-05-04于兆华王丽红王成国
于兆华,王丽红,李 强,王成国
(1 中国铁道科学研究院 标准计量研究所,北京100081;2 郑州铁路职业技术学院,河南郑州450052;3 北京交通大学 机械与电子控制工程学院,北京100044;4 中国铁道科学研究院 铁道科学技术研究发展中心,北京100081)
目前大秦铁路使用的17号钩尾框为改进后的锻造E级钢钩尾框,其性能较原有的铸造E级钢钩尾框有所提升,但大秦铁路上机车的牵引总重由原来的5千t增加至现在的2万t,牵引总重的增加使车辆的纵向牵引载荷及冲击载荷均大幅增加,车钩缓冲装置部件的疲劳寿命显著下降,短期内即有大量的钩尾框因尾部弯角处疲劳裂纹长度超限而报废。目前,二维裂纹问题己有许多成熟分析方法,对于含三维裂纹的有限大物体,目前只有少量应力强度因子数值解,含三维裂纹的服役构件,裂纹尖端应力强度因子的计算就更加复杂,可直接用来计算应力强度因子的方法尚不多见[1]。本文应用1/4点位移法,在三维模型上建立裂纹模型,直接计算应力强度因子,并对形状系数进行拟合,然后根据AAR载荷谱采用Paris公式计算了钩尾框的裂纹扩展寿命。
1 应力强度因子简介及计算方法选取
当物体内存在裂纹时,裂纹尖端应力在理论上为无穷大,裂纹尖端是一个奇点。因此不能用理论应力集中系数Kt来表达,而必须用应力场强度因子K来表达。K的大小反映了裂纹尖端附近区域内弹性应力场的强弱程度,可以用来作为判断裂纹尖端是否发生失稳扩展的指标。
对于一般的情况,其应力强度因子表达式的普遍形式为:

式中Y为决定于裂纹体形状、裂纹形状、裂纹位置与加载方式的系数,它可能是常数,也可能是a的函数;a为裂纹尺寸,对于内部裂纹和贯穿裂纹而言为裂纹的半长度,对于表面裂纹而言为裂纹的深度[2];σ为裂纹处的名义应力。
1/4点位移法是将临近裂纹尖端单元的中心点移到1/4点处,从而构建与线弹性断裂力学理论相似的1/r奇异性,由于其运用较简便、实用,且精度在位移解法中最精确,因而逐渐地被广泛应用。Barsoum证明了它的有效性和精确性[3],本文以1/4点位移法对钩尾框表面裂纹疲劳扩展的应力强度因子进行计算。
2 钩尾框应力强度因子计算
2.1 钩尾框静强度计算
锻造E级钢钩尾框具有对称结构,三维模型见图1,因此可以取1/4模型进行分析,对该模型采用二阶4面体单元和二阶6面体单元进行有限元网格划分,划分完成后有限元模型见图2,模型总单元数25 017个,其中C3D20单元为8 790个,C3D10单元为16 227个,总节点数为66 473个。
在钩尾框前端销孔处施加位移约束,在钩尾框尾部承载平面(与后从板接触处)上施加纵向牵引载荷,在模型对称面处施加对称约束。采用ABAQUS软件进行有限元计算,在牵引载荷为1 000 kN(由于钩尾框所受载荷不为定值,进行强度计算时取1 000 kN,其他载荷下的应力进行线性折算)时钩尾框有限元Von Mises应力和X方向的应力如图3和图4所示,最大合成应力及X方向的应力发生在钩尾框尾部弯角处及靠近尾部弯角的框身附近,且X方向的拉应力占绝对主导,最大合成应力为344 MPa。

图1 钩尾框三维模型

图2 钩尾框有限元模型

图3 Von Mises应力
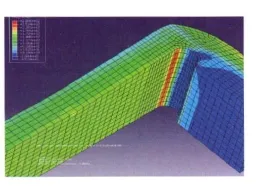
图4 尾部弯角区域X方向的拉应力
2.2 钩尾框应力强度因子计算
由钩尾框静强度分析可知,与裂纹面垂直的拉应力占主导地位,靠近裂纹前沿的应力状态以平面应变为主,因而可认为钩尾框裂纹属于平面应变状态下的I型裂纹。
由钩尾框静强度计算、文献[4]及钩尾框运用中发生裂纹的实际情况可知,钩尾框裂纹主要发生在钩尾框尾部弯角与框身过渡处,钩尾框表面裂纹可以看作是处于钩尾框尾部弯角中部的半椭圆型裂纹和钩尾框尾部弯角上下面的1/4椭圆角裂纹,裂纹位置示意图见图5、图6。
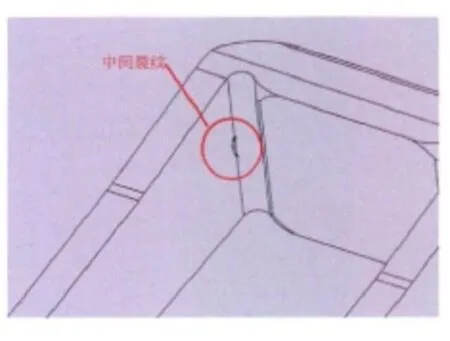
图5 钩尾框中间裂纹示意图
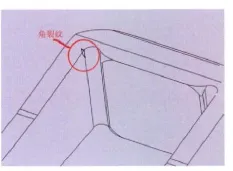
图6 钩尾框角裂纹示意图
采用有限元计算应力强度因子时,为了真实模拟裂纹前缘应力应变场,需要将裂纹前缘区域划分为很小的单元。如果采用整个钩尾框模型进行有限元网格划分,会使模型的单元数量增多,造成模型求解困难。为了解决上述矛盾,本文截取钩尾框尾部弯角和附近框身,建立简化的含表面裂纹的有限元模型进行裂纹扩展分析。对钩尾框取1/4模型进行简化,简化后模型见图7。为了验证简化后模型的计算结果正确性,在不引入裂纹的前提下对简化后模型划分6面体网格,在图7所示的Y-Z平面上施加X方向的位移约束,其他约束及载荷施加同静强度计算,计算结果显示最大应力位置未发生变化,最大合成应力为341.5 MPa,因此该简化模型满足计算要求。
由于ABAQUS软件计算带裂纹体的应力强度因子只能够使用6面体单元,本文对图7所示模型进行二阶6面体单元网格划分,划分完成后裂纹网格模型见图8。在ABAQUS中定义裂纹的裂纹前沿和扩展方向,指定半椭圆裂纹的半椭圆边界为裂纹前沿,图7所示模型的Z轴方向为裂纹扩展方向,划分完成的带有裂纹体的有限元模型见图8。
利用ABAQUS软件,采用1/4点位移法进行应力强度因子计算,裂纹尺寸及计算结果见表1(此处,a为半椭圆裂纹深度,c为半椭圆裂纹长度之半)。横坐标表示,纵坐标表示应力强度因子K,则钩尾框应力强度因子与关系见图9。在图9中,上部3条线代表中间裂纹,下部3条线代表角裂纹,从图中可以看出应力强度因子随的值近似线性变化,因此可以将公式(1)中的Y值当做定值处理。对于钩尾框尾部弯角处裂纹,线性拟合得到中间裂纹的系数Y=0.683,角裂纹的系数为Y=0.443。

图7 钩尾框结构简化后模型图

图8 钩尾框裂纹网格模型

表1 钩尾框裂纹尺寸与应力强度因子

图9 钩尾框裂纹尺寸与应力强度因子关系
3 钩尾框疲劳裂纹扩展寿命
中国铁道科学研究院曾在2005年采集过大秦线载荷谱,但当时采集得到的载荷谱由于测试条件以及测试侧重点不同,不适合用来进行17号钩尾框的裂纹扩展寿命计算,而大秦线重载货运列车的运行条件和美国AAR载荷谱的采集条件有许多相近之处,因此计算大秦线重载列车钩尾框的裂纹扩展寿命时,采用AAR北美铁道协会标准汇编CⅡ分册当中规定的90.7 t漏斗车重车车钩载荷(线路环境)载荷谱(以下简称AAR载荷谱)。该载荷谱谱长23 797 km,载荷循环总数为85 679次,平均每公里循环为3.6次。
初始裂纹尺寸a0是指开始计算寿命时的最大原始裂纹尺寸,可以用无损探伤方法检测出来。初始裂纹尺寸的大小,与探伤技术的发展及探伤人员的技术水平有关。本文中计算裂纹扩展寿命时,取钩尾框的初始裂纹尺寸为a0=0.5 mm。
计算裂纹扩展寿命常用的公式为Paris公式:

式中C、m为常数,Δ K 是应力强度因子幅值,其定义为:

ΔS是裂纹处的名义应力幅值。由线弹性理论,可以根据载荷谱的每一级载荷计算出对应的最大应力和最小应力,代入公式即可求得每一级载荷对应的ΔK。
由于在压缩载荷时,应力强度因子K无定义,因此在载荷谱中,压缩载荷对应的应力强度因子K=0。
当应力强度因子幅值ΔK<ΔKth时,裂纹不扩展,Δ Kth称为裂纹扩展的门槛值。平均应力对门槛值有较大影响,其影响可用下式表示为:

式中ΔK′th为应力比为R时的门槛值;ΔKth为应力比 R=0时的门槛值;m′为材料常数,一般为1/2[2]。对于E级钢,查文献[5],取门槛值 ΔKth=6.57 MPa,取m′=0.5,将 ΔKth=6.57代入式(4)得
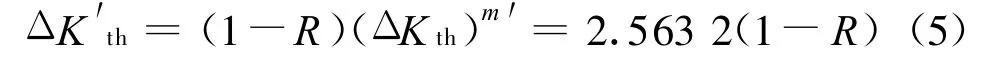
在进行钩尾框裂纹扩展寿命计算时,门槛值按照式(5)计算。
对于钩尾框,按照TB/T 2703-96《回转和固定式联锁车钩、钩尾框技术条件》规定,焊修最大深度不得超过25.4 mm,因此取临界裂纹尺寸=25.4 mm。同时由文献[3]知,对于 E级钢,断裂韧度=53.4 MPa,因此在计算钩尾框裂纹扩展寿命时,采用ac和Kc两个判据进行判断,当其中一个达到时,即认为钩尾框断裂。
对于E级钢,采用文献[3]中提供的裂纹扩展数据,即取公式d=C(ΔK)m中的C=6.5×10-10,m=2.28。
对Paris公式积分,可得疲劳裂纹扩展寿命为:

若形状因子Y与裂纹尺寸a无关,则
当m≠2时,
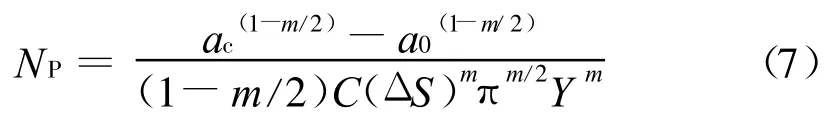
将上式进行变换,则
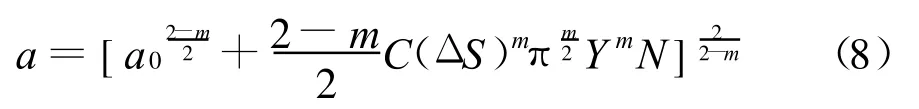
式(8)的含义是在名义应力幅值为ΔS、初始裂纹尺寸为a0、裂纹处构件形状系数为Y的条件下,经过N次加载后,裂纹的尺寸扩展为a。
钩尾框承受的载荷是随时间变化的,在将它承受的实际载荷编制为应力谱后,可以将其加载情况看作是在一个谱块内,应力由小到大,顺序作用,钩尾框承受完一级应力作用之后,再去承受下一级应力。因此,在一个谱块中,将一级应力作用完导致裂纹扩展后的尺寸作为下一级应力的初始裂纹尺寸。一个谱块作用完之后的裂纹尺寸,作为下一个谱块开始作用的初始裂纹尺寸。
采用MAT LAB编制程序进行计算,计算结果见表2。由表2可知,当钩尾框裂纹为角裂纹时,裂纹扩展寿命较长,当裂纹处于中间位置时,裂纹扩展寿命较短。对于中间裂纹,当运行到第13个谱块时,裂纹尺寸超过临界裂纹尺寸;对于角裂纹,当运行到第48个谱块时,裂纹尺寸超过临界裂纹尺寸。
4 结束语
从17号钩尾框的裂纹扩展寿命计算结果可以看出,钩尾框裂纹扩展速率随着裂纹尺寸的增大而增大,为了提高钩尾框的使用寿命,应当尽量抑制裂纹萌生与小裂纹的产生,防止裂纹的急剧扩展。在实际运用当中,应当制定合理的检修制度,当钩尾框裂纹超过一定尺寸时,应当立即将钩尾框进行更换或焊修,避免钩尾框在运用中裂纹急剧扩展,造成钩尾框断裂事故。采用Paris公式计算得出的钩尾框的裂纹扩展寿命,可以根据实际情况,考虑一些安全系数,将裂纹扩展寿命除以一个安全系数得到保守的运行公里数,为制定合理的检修周期提供重要的依据。
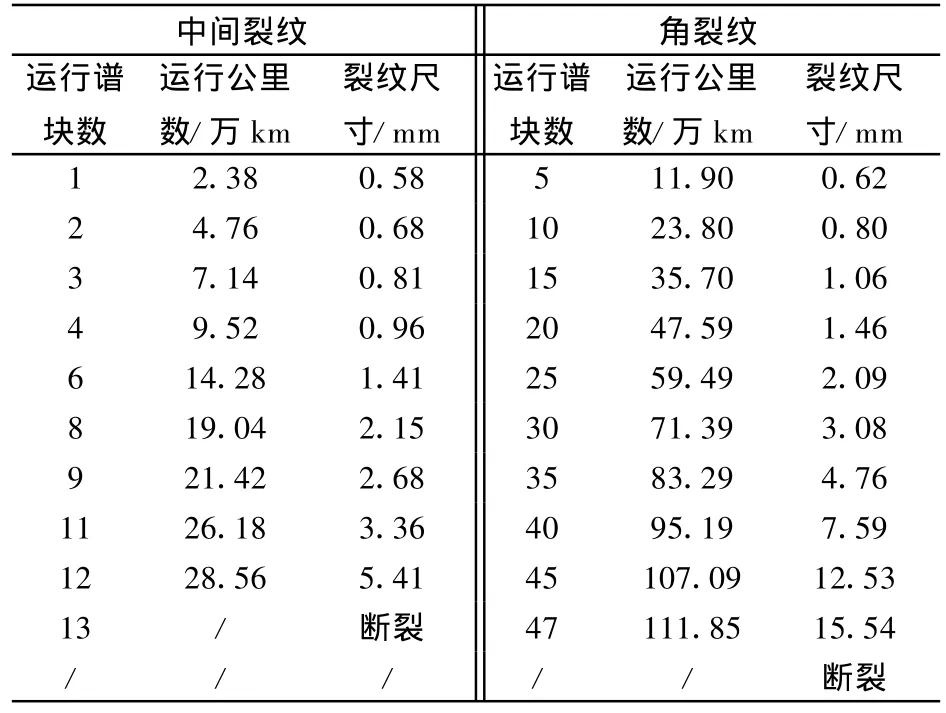
表2 钩尾框裂纹扩展寿命
[1] 刘青峰,谢基龙,缪龙秀,等.钩尾框尾部弯角疲劳裂纹扩展寿命预测研究[J].铁道学报,2002,24(5):42-46.
[2] 李舜酩.机械疲劳与可靠性设计[M].北京:科学出版社,2006.
[3] 李晓慧.重载列车钩舌疲劳裂纹萌生与扩展特性研究[D].北京:北京交通大学,2006.
[4] 刘青峰.疲劳裂纹扩展仿真技术研究及在车辆工程中的应用[D].北京:北京交通大学,2004.
[5] 赵少汴,王忠保.抗疲劳设计——方法与数据[M].北京:机械工业出版社,1997.
