布雷顿与斯特林联合循环ECOP性能分析

何远令，龚建政，贺 星，陈立强

(1.海军工程大学,武汉 430033;2.91204部队装备部，广东台山 529267)

1 引言

有限时间热力学[1-4]是分析、优化热机循环性能的重要理论，在用来分析、优化热机循环时，除了以功率[5]、效率[6]为目标以外，还有其他多种选择，如比功率[7,8]、经济性[9、10}等。

文献[11]在研究热机时，综合考虑了热机的输出功率P以及低温热源温度TL和循环的熵产率σ，提出以作为生态学最优目标。这虽然考虑到了功率与能量的关系，但在本质上并没有把能量(热量)与功区别对待。

燃气轮机简单布雷顿循环在实际运行中所产生的大量的具有一定温度的废气可再利用，而斯特林机具有热端温度要求不高、效率高等优点。基于此，本文以1个新型的“布雷顿—斯特林”联合循环为研究对象，分析考虑在有热阻和热漏的情况下，用1种新的目标，即生态学性能系数 ECOP[14]，来分析并研究各种参数对联合循环性能的影响。

2 联合循环理论模型

由内可逆的布雷顿循环与斯特林循环组成的联合动力循环如图1所示。其中，1－2－3－4－1为布雷顿循环，1－2、3－4为等熵过程，2－3、4－1 为等压过程；5－6－7－8－5 为斯特林循环，5－6、7－8 为等容过程，6－7、8－5 为等温过程，其热腔和冷腔的工作温度分别为TH2和L2。高、低温热源温度分别为TH和TL，高、低热源间存在直接热漏Qi。在4－1的等压放热过程中，高于斯特林热机热腔工作温度TH2的部分热量可以被斯特林循环工质吸收，并以等效平均放热温度TL1表示；TL1″表示低于TH2的部分热量的等效平均放热温度。TH1为2－3等压吸热过程中的等效平均放热温度。联合循环中的温度梯度为：TH＞ TH1＞ TL1＞TH2＞ TL1″＞TL2＞TL。图1的联合循环中的T-S图可简化，如图2所示。

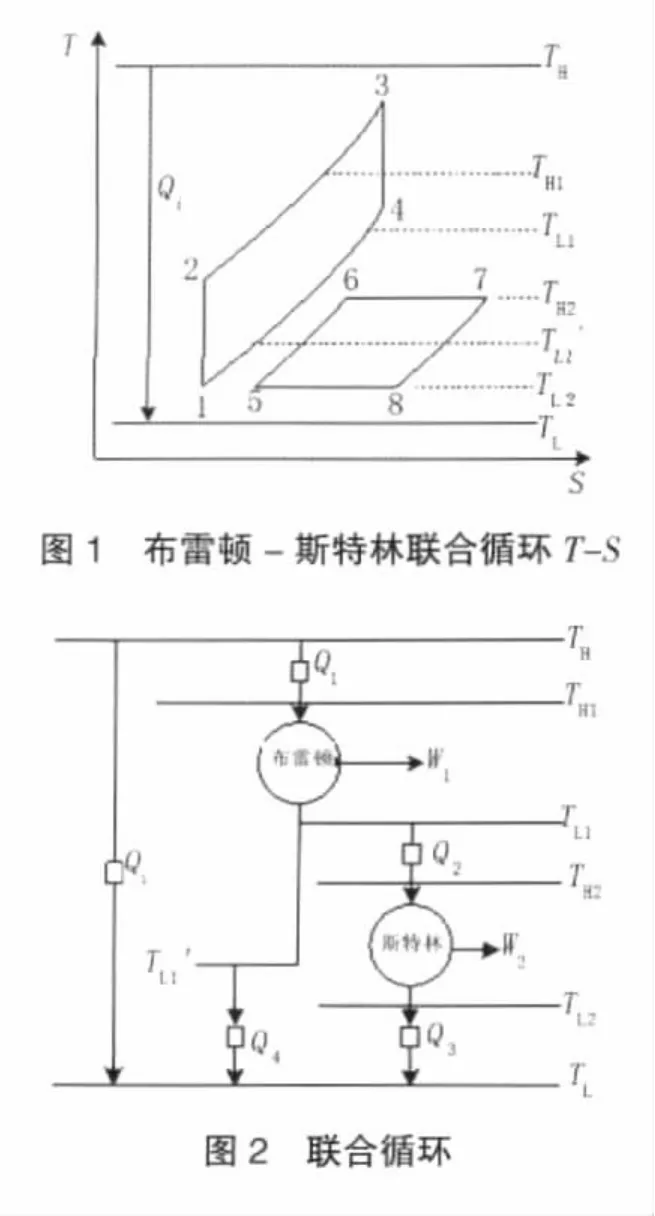
3 循环分析

假设工质与热源间换热器为逆流式，工质与热源间的传递遵循牛顿传热律，由热交换理论可得联合循环的热力学模型

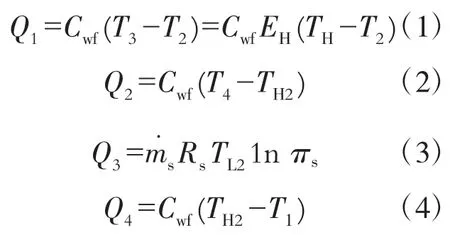
式中：Cwf为布雷顿循环中工质的热容率（质量流率与比定压热之积）；EH为布雷顿循环中高温侧换热器的热有效度，EH=1-exp(-NH)；NH为传热单元数，NH=UH/Cwf；m˙s为斯特林热机中工质的质量流率；πS为斯特林热机中工质的气体常数；为斯特林热机中工质的压缩比。

设压气机压比为，则

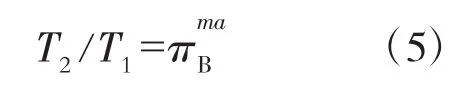
式中：ma=(γa-1)/γa。

由式(1)和式(5)可得

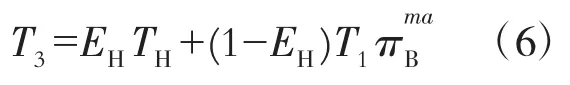
布雷顿内可逆循环4个温度的关系为：T1T3=T2T4，结合式（5）和式（6）可得

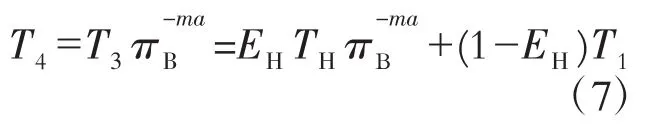
由于布雷顿循环高温部分放热量等于斯特林循环的吸热量，则

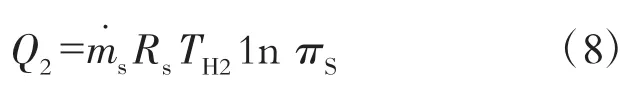
由式（2）、（7）和式（8）可得

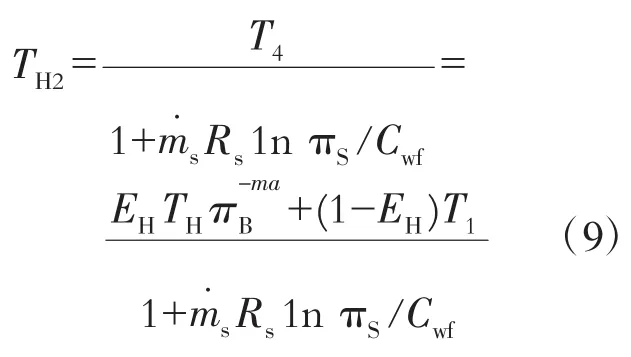
由功率P=Q1-Q3-Q4可得

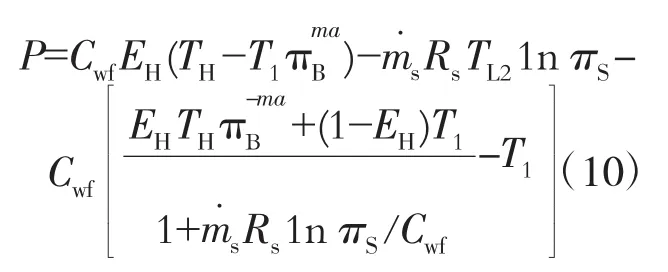
设高、低温侧热源间存在直接热漏，热漏流率 Qi=Ci(TH-TL)，为热漏系数。则由熵的定义可得联合循环中各过程的熵产

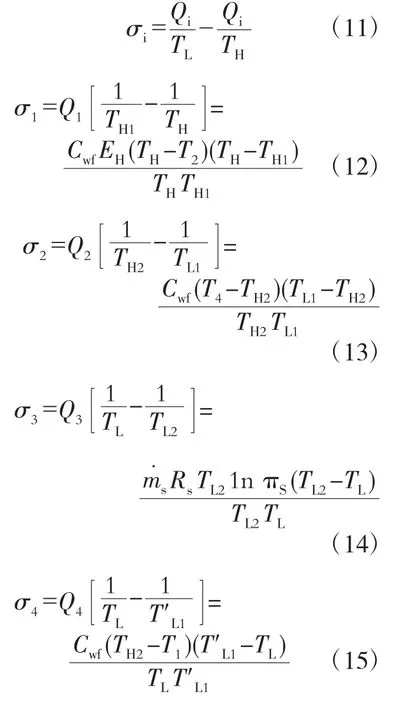
由平均温度的定义可知2－3过程的熵产

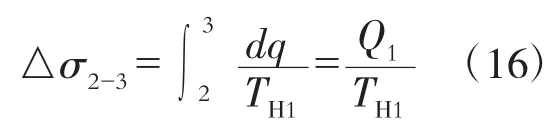
又2－3是定压过程，则

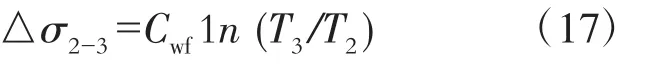
联立式（1）、（16）、（17）可得

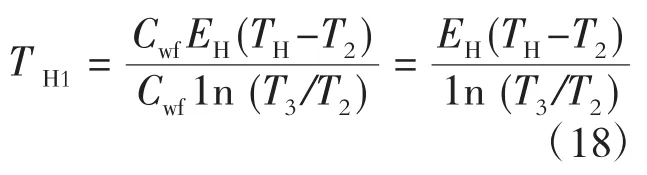
同理可得

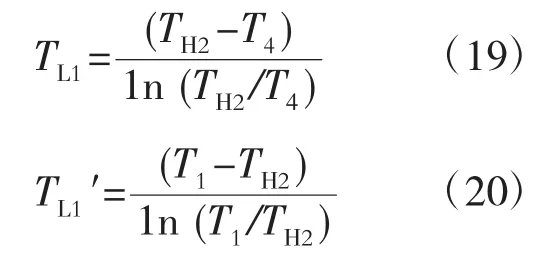
由此可得总熵产

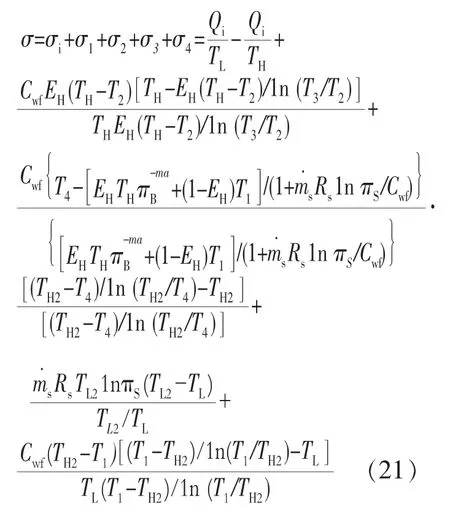
生态学性能系数ECOP=(A/t)·(T0σ)。式中：A为循环输出；T0为环境温度；σ为循环熵产；t为循环周期。对热机而言，循环输出等于输出功，即：A/t=P，则

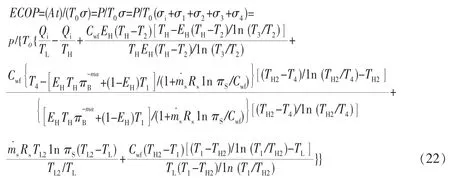
4 数值计算及分析

取 TH=1500 K，TL=300 K,T0=280,TL2=350 K，T1=320 K ，EH=0.9，Cwf=1 kW/K ，γα=1.4，RS=2.078 kJ/(kg·K)，=0.1 kg/s，π=2 ，SCi=0.1为基准值，进行数值计算分析。

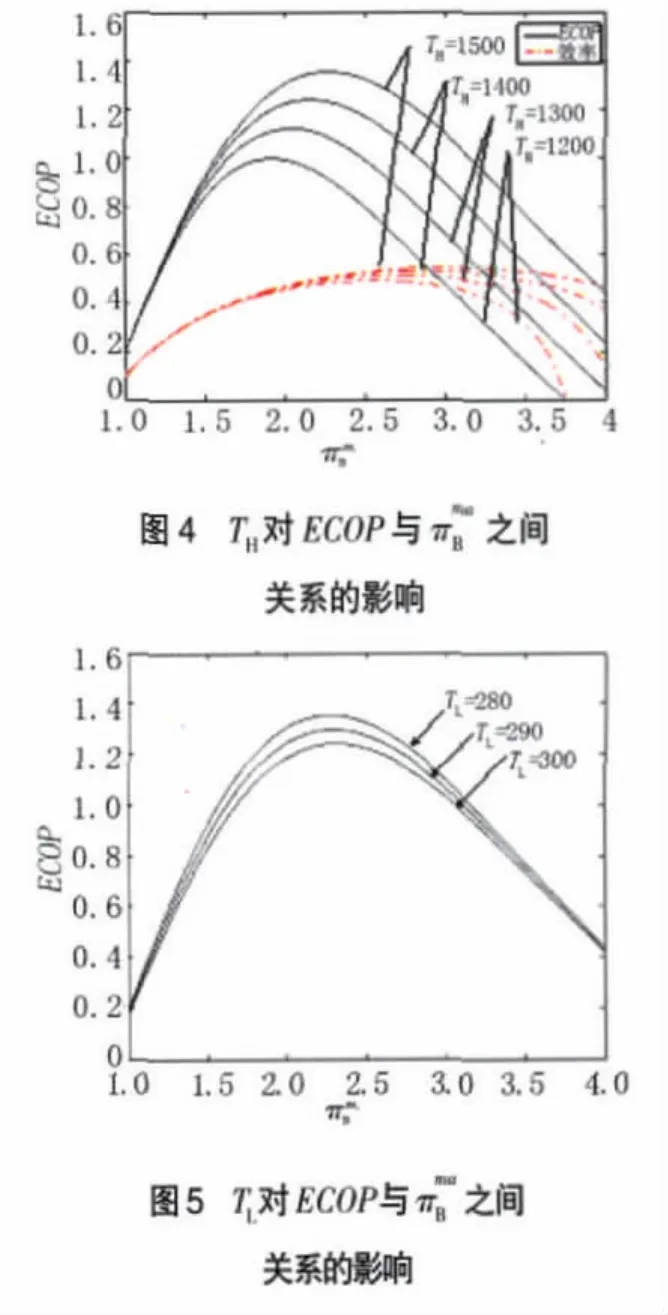
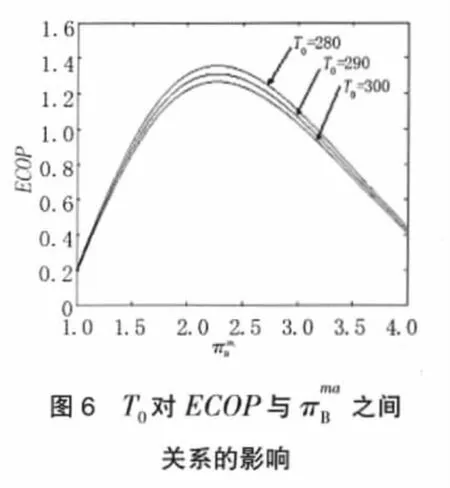
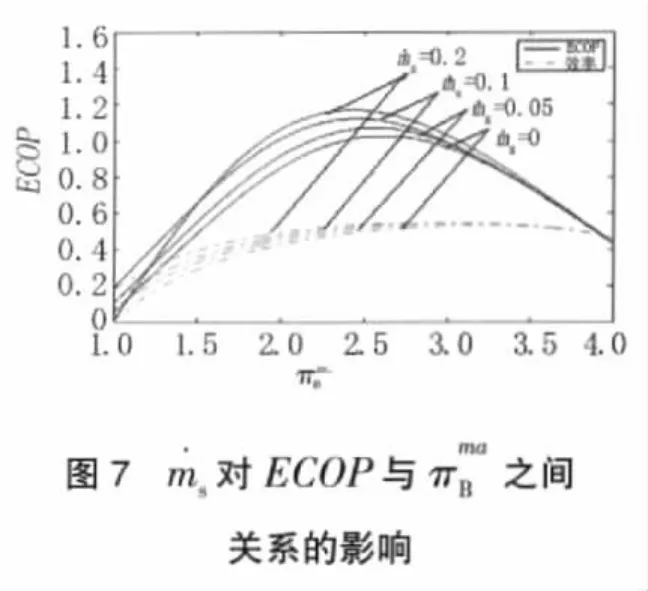
图 3～7 分别给出了在Ci、TH、以及低温热源TL和环境温度T0取值不同时，对生态学性能系数ECOP与工质温比之间关系的影响。作为对照和比较，同时在图中也显示了效率η与工质温比之间关系的曲线。计算表明：随着工质温比的增大，ECOP有峰值，在=2.3时（即压比约为18.5时），ECOP达到最优。从图中可知，ECOP随 T、和π的H增大而增大，而随Ci、T0的增大而减小。

图3给出了热漏Ci对ECOP与之间关系的影响。由图中可知，Ci对ECOP有明显的影响，在理想状态下（Ci=0时），ECOP的值接近2；当存在热漏时（Ci＞0）,ECOP 明显减小；Ci从 0增大到0.2时，ECOP的最大值从1.9减小到1.02，减小了46.32%。由此可见系统热漏被削弱的程度对ECOP至关重要。通过比较可以看到ECOP的变化范围更大，作为热机设计的目标时，选用ECOP指标更加直观。

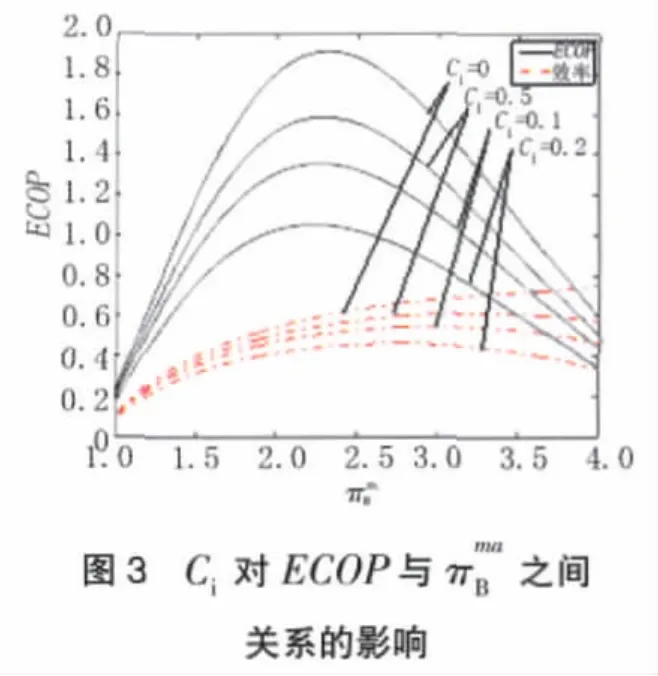
图 4～6 分别给出了 TH、TL、T0取值不同时对温比ECOP与之间关系的影响。由图中可知，提高热腔温度或者降低冷腔温度都能使联合循环的ECOP明显增大。从图6中可知，环境温度对ECOP也存在着一定影响，这是因为环境温度会改变系统的，从而使循环中在环境温度下不可能转化为有用功的那部分能量发生变化，ECOP也随之改变，二者之间成反比关系。

5 结束语

作为热机设计的目标，ECOP是1个有用的备选方案。

[1]Ch en L,Wu C,Sun F.Finite time thermodynamic optimization or entropy generation minimization of energy systems[J].J Non-Equilib Thermodyn,1999,24(4):327-359.

[2]Chen L,Sun F.Advances in Finite Time Thermodynamics Analysis and Optimization [M].New York:Nova Science Publishers,2004.

[3]陈林根.不可逆过程和循环的有限时间热力学分析[M].北京:高等教育出版社,2005：280.

[4]Bejan A.Entropy generation minimization:The new thermodynamics of finite-size device and finite-time processes[J].J Appl Phys,1996,79(3):1191-1218.

[5]Curzon F L,Ahlborn B.Efficiency of a Carnot engine at maximum power output[J].Am J Phys,1975,43(1):22-24.

[6]Gutomicz-Krusin D,Procaccia J,Ross J.On the efficiency of rate processes:Power and efficiency of heat engines[J].J Chem Phys,1978,69(9):3898-3906.

[7]Wu C.Specific power bound of real heat engines[J].Energy Convers.Mgmt,1991,32(3):249-253.

[8]Agnew B,Anderson A,FrostT H.Optimization of a steady-flow Carnot cycle with external irreversibilities for maximum specific output[J].Appl.Thermal Engng,1997,17(1):3-16.

[9]陈林根，孙丰瑞，陈文振.两源热机有限时间火用经济性能界限和优化准则[J].科学通报，1991，36(3):233-235.

[10]De Vos A.Endoreversible Economics[J].Energy Convers.Mgmt,1997,38(4):311-317.

[11]Angulo-Brown F. An ecological optimization criterion for finite-time heat engines[J].J Appl Phys,1991,69(11):7465-7469.

[12]陈林根,孙丰瑞,陈文振.热力循环的生态学品质因素[J].热能动力工程,1994,9(6):374-376.

[13]Chen L,Zhou J,Sun F,etal.Ecological optimization for generalized irreversible Carnot engines [J].Appl.Energy,2004,77(3):327-338.

[14]Ust Y,Sahin B,Sogut O S.Performance analysis and optimization of an irreversible dual-cycle based on an ecological coefficient of performance criterion[J].Appl Energy,2005,82(1):23-39.