秦山核电站二期反应堆堆芯流量分配数值分析

张曙明,李华奇,赵民富,陈玉宙,杨 夷,卫光仁

(1.中国原子能科学研究院,北京 102413;2.中国核动力研究设计院,四川 成都 610041)

压水堆热工水力性能的改善迫切需要获得可靠的堆芯入口流量分配数据[1-8]。20世纪80年代后期,西屋公司四环路压水堆多次出现堆芯出口温度增加以及堆芯流量降低等异常工况。西屋公司认为下腔室内漩涡的形成与耗散是产生这些异常现象的主要原因[9]。下腔室内工质的流动状况对堆芯入口处流量分配的影响较大：工质自环形下降段进入下腔室形成的射流导致流动分离,出现漩涡脱落现象,在堆芯边缘处下方产生低压区,进而导致堆芯入口处流量分配不均匀。Yeh曾尝试应用理论分析方法计算下腔室的速度分布,将势场分为若干区求得三维情况下的势场解[10]。因反应堆内几何结构所致,堆内工质的流动呈现出极其复杂的流动特征,精确解析解很难获得。从国内外已公开的研究成果来看,研究工作多集中于不同比例的小尺度模型实验[1-9],成本非常昂贵且耗时耗力。

近年来,在反应堆内流场CFD数值计算领域,国内外研究人员相继开展工作并取得一定的进展[8,11-19]。然而,研究工作并非基于全部压力壳区域展开。计算区域往往局限于环形下降段、下腔室与部分堆芯燃料组件区域;由于缺乏对压力壳内工质流动特性的足够了解,对模型进行了不适当的简化。本文工作以秦山核电站二期反应堆整体水力模拟实验模型为研究对象,通过对反应堆内流场进行计算分析,探索对反应堆整体几何结构模拟与合理简化等关键问题的数值研究策略和方法。

1 计算模型

1.1 600 MW电站堆整体水力实验模型

600MW电站堆整体水力模型在国内首次采用了棒束开式栅格设计。该实验模型建于中国核动力研究设计院,其结构示意图如图1所示,模型尺寸为电站堆原型的1/4。同时,在对流场影响不大的情况下对原型结构进行了必要简化[5-7]。

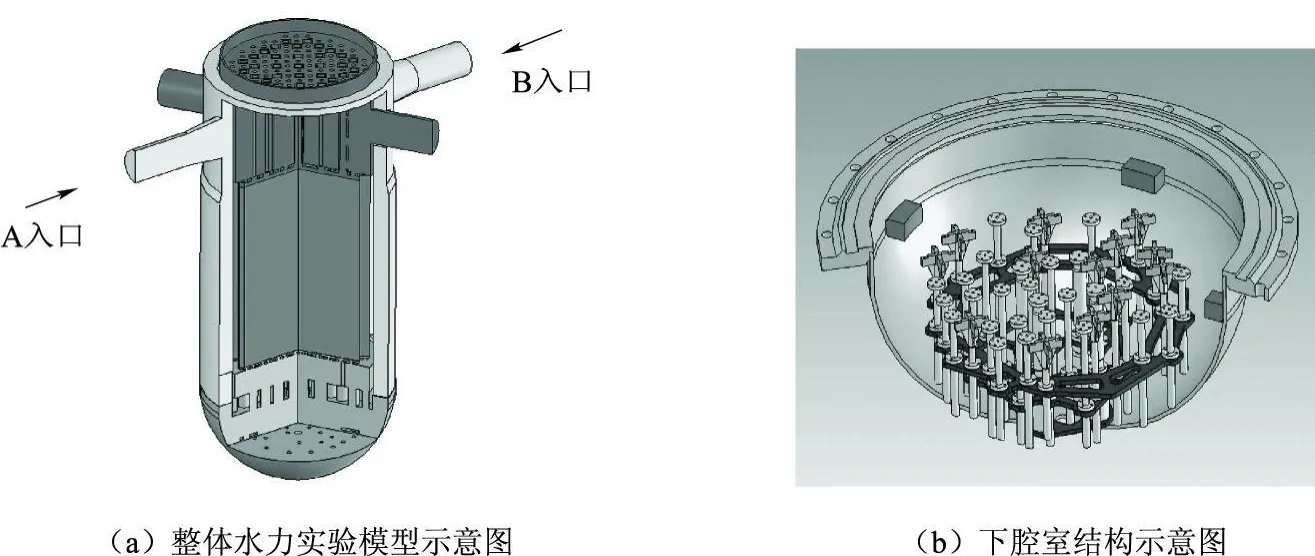
图1 整体水力实验模型Fig.1 Integralhydraulic testmodel

1.2 几何建模及网格划分

计算模型结构复杂,给网格划分和计算求解工作带来较大困难。主要体现在以下方面：

(1)结构件众多：在工质的沿程流动方向上,整个计算区域包括2个入口管、环形下降段、下腔室及内部组合支撑架、下支撑板、堆芯下板、模拟燃料组件、堆芯上板和2个出口管,以及众多测量、机械装配体等附加几何结构件。这些部件几何形状各异,建模难度相应大为增加。

(2)各部件几何尺度差异明显：整体水力模型几何尺度较大,高度为2 264 mm,外径为960mm,然而模型内又存在数量相当多的窄间隙。以121组2×2模拟燃料组件形成的子通道为例,元件棒间间隙仅为6mm,下腔室内部结构也存在许多类似情况,如何较真实地还原再现流动现象是面临的计算难点之一。

(3)无整体对称性：整体模型中,仅堆芯区域具有几何对称性。下腔室内组合支撑架(图1b)、环形下降段内的热屏蔽等结构使得几何对称性无法满足。借助对称性以便简化计算域的技术手段无法采用,整体模拟在所难免。因此,必须在计算精度与网格数量规模这二者之间取得较好的平衡。

考虑计算机现有硬件能力,建模过程作以下简化：

(1)水力模型内部的一些装配固定机械零件,如螺栓、十字肋板等部件对整体流场的影响很小,建模时对此类结构件不予考虑。

(2)模拟燃料组件由121组排列为2×2的棒束及上下管板组成,内部包括数量众多的涡轮流量计与测量引线。

在现有硬件水平范围内模拟此类结构,引入多孔介质模型处理。

在简化模型时还运用了一些技术策略,包括：

(1)分区生成网格：鉴于下腔室存在大量复杂结构件,全部使用结构化网格划分所有计算区域既不现实也无必要。因此,计算采用结构化和非结构化混合网格技术。将整个计算区域分割为如图2所示的4个区域,在CFD求解器中采用交接面衔接各自区域。某种程度上,交接面的存在降低了计算速度与精度。但通过对各区域分别选择不同的网格类型进行网格划分,极大地降低了网格划分的难度。4个区域分别是：环形下降段、下腔室、堆芯和上腔室。除下腔室之外,其余均采用结构化网格划分。

图2 计算区域Fig.2 Com putational domain

(2)平衡网格数量与质量：环形下降段和上腔室中,对流动变化剧烈的区域宜布置更细密的小尺寸结构化网格,其余位置则兼顾网格的数量,布置了较大尺寸的结构化网格;对几何结构复杂的下腔室区域,原则上宜布置数量较多的非结构化网格以便真实描述其几何形状。通常非结构化网格所消耗的计算机资源是相同结点数结构化网格的2倍,因而非结构化网格数量不可过多。但若网格布置数量过少,将会造成对下腔室几何结构描述失真,引起网格质量下降,影响计算结果的可靠程度。因此,在确保各流道截面至少布置6个网格的前提下,进行多次划分方能最终生成数量与质量均理想的网格。

1.3 下腔室结构敏感性研究

对各部分计算域划分网格,下腔室区域的网格数目所占比例较大,网格总数难以控制在合理范围内。经分析,初步判断下腔室内3块格架板对计算结果的影响有限,而且其复杂结构直接导致网格总数剧增直至超出现有常规计算机硬件要求,计算将难以进行。因此,对下腔室区域单独采取几何结构敏感性计算分析。根据计算结果验证格架板对工质流动的影响,进一步对下腔室结构进行合理简化。为此,分别按下腔室单格架板、双格架板以及3格架板建立计算区域模型(图3)。为图中示意清楚起见,下腔室结构与原型不同,其球形下封头在图中略去(下同)。

网格尽可能布置较密以便更真实反映下腔室几何外形,从而提高计算精度。其中,单格架板网格数目约为254万,双格架板网格数目约为232万,3格架板网格数目约为229万。篇幅所限,仅列出3格架板网格分布情况(图3d)。流动工质为水,温度40℃,压力 0.5M Pa,视为单相、不可压缩流体的等温稳态流动。如图3a所示选定出、入口,其边界条件设为：速度入口2.2m/s,压力出口0.5MPa。模型内工质流动雷诺数Re量级约为106,选用标准k-ε两方程湍流模型及壁面函数法进行求解。

图3 反应堆下腔室示意图Fig.3 Schematic of lower plenum

1.3.1 计算结果比较

针对3种不同下腔室结构,对部分堆芯入口归一化流量进行了量化比较。归一化流量qi定义为：

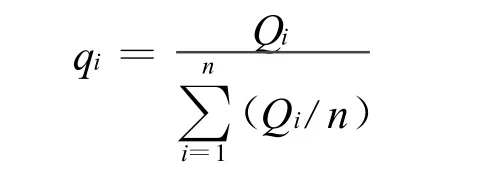
式中：Qi——i组件入口流量;

n——模拟组件数。

堆芯区域共121组模拟组件,限于篇幅,本文选取自堆芯中部至堆芯边缘(1-1至1-8,2-1至2-8,3-1至3-5,如图4a所示)21组模拟组件的堆芯入口归一化流量进行比较。计算结果表明,具有代表意义的21组组件内的流量分布受格架板结构影响较小(图4b)。因此,对下腔室结构最终仅保留单格架板建立模型进行计算。

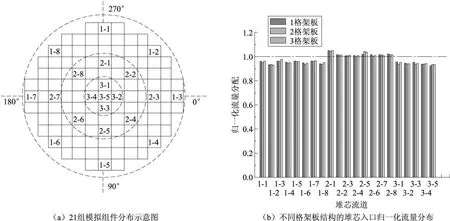
图4 21组模拟组件的堆芯入口归一化流量分布比较Fig.4 Comparison o f flow distribution factors at the core in let with different support plate

2 CFD计算结果

2.1 计算条件设定

计算区域最终生成网格如图5所示,总计187万网格。其中下降段网格数为34万,下腔室网格数为145万。相应边界条件如下：

(1)入口取在冷管段入口管嘴处,设定为法向速度入口边界条件。根据不同环路流量工况,冷管段入口来流法向速度分别设为5.81 m/s、10.21 m/s 、10.44 m/s。

(2)出口取在上腔室出口管嘴处,设为0.5 MPa。

(3)固体壁面设为无滑移边界条件。

2.2 多孔介质模型

对于堆芯区域,引入多孔介质模型,即将堆芯内部视为多孔介质进行处理,不需要对复杂的内部结构进行细致描述[20]。对于堆芯流道,不考虑渗透率的阻力影响,将全部的压降归结为形阻和摩阻。通过已知的堆芯压降实验测量值,将阻力系数转换为当地阻力系数。横向阻力大小受主流惯性力与堆芯元件几何结构的影响很大,其数据多通过实验获得[21-22]。不失一般性,本研究中横向阻力系数采用沿程方向阻力系数的倍数关系,其数值取为10。

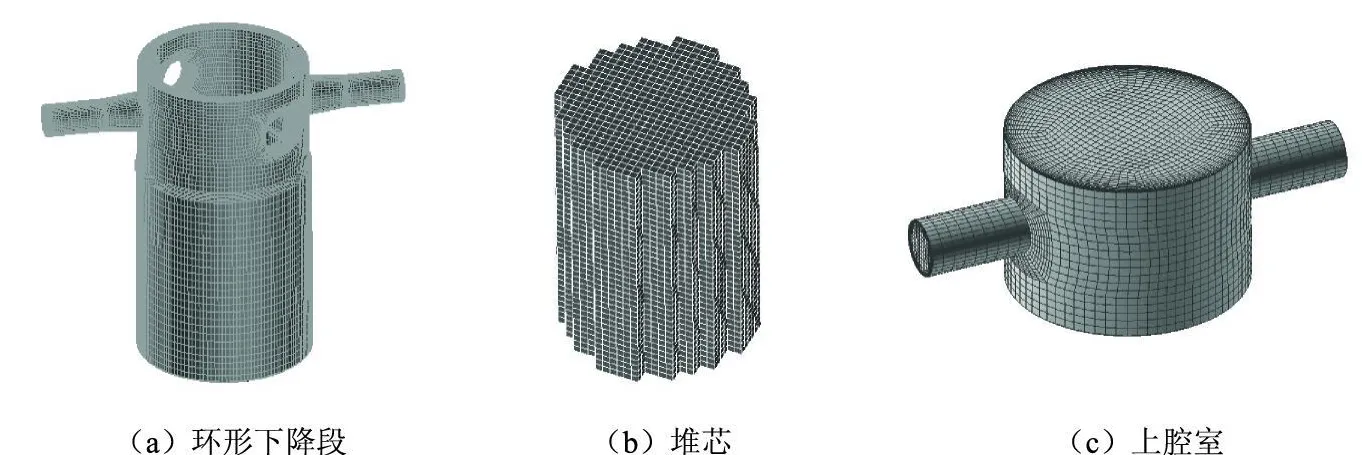
图5 计算区域网格Fig.5 Com puter grid generation

3 计算结果与分析

计算收敛性的判断参照以下依据：

(1)算例中各参数残差均小于10-5。

(2)计算区域出、入口满足质量守恒要求。

(3)选取计算区域中不同位置进行监测直至压力基本保持不变。

采用CFX软件进行单机计算,PC机CPU主频2.8G,内存4 G,约需12 h可达到收敛。下面结合压力壳内速度矢量分布、流线分布和堆芯入口流量分配等计算结果分别加以分析。

3.1 双环路工况流场分布

3.1.1 双环路工况下降段流场分布

双环路运行工况下,流体从2个入口管嘴流入反应堆压力容器后,受环形下降段结构形状所限,分别呈辐射状向吊篮壁面强烈冲击(图6)。之后流体呈外“八”字形状分成2股向下腔室方向流动,并在约1/2下降段高度的出口管嘴下方处开始汇合。在该工况下,环形下降段流场基本呈对称态势分布。

3.1.2 双环路工况下腔室流场分布

流线分布结果展示了流体进入反应堆压力容器后的流动线路,自A、B入口管嘴分别流入的流体在下降段汇合,下腔室流体出现180°转向并发生强烈混合作用这一过程得以更为清晰地反映(图7)。同时,可清楚观察到双环路运行工况时,下腔室出现流动滞止区,存在2个较明显的漩涡(2对)。

图6 双环路工况下降段流场分布Fig.6 Flow field in the dow ncomer under tw o-loop operation

图7 双环路工况流线分布Fig.7 Stream line distribution under tw o-loop operation

3.2 单环路工况流场分布

3.2.1 单环路工况下降段流场分布

如图8所示,单环路运行工况下,流体从入口管嘴流入反应堆压力容器后,与双环路运行工况相类似呈辐射状向吊篮壁面强烈冲击。之后流体同样分成2股向下腔室方向流动,并于对侧入口下方开始汇合,这与双环路运行工况下的流场分布相比明显不同。

图8 单环路工况下降段流场分布Fig.8 Flow field in the dow ncomer under sing le loop operation

3.2.2 单环路工况下腔室流场分布和流线分布

单环路运行工况时,下腔室仅有2个较明显的漩涡生成,漩涡出现的位置与强度大小较双环路运行工况均有很大差别(图9)。

图9 单环路工况流线分布Fig.9 Stream line distribution under single loop operation

3.3 堆芯入口流量分配结果

由表1可以看出121组模拟组件中,双环路工况下大多数堆芯入口流量都分布在平均流量95%～105%的范围内,约占组件总数90%左右。在秦山核电站二期工程反应堆热工水力设计中,堆芯入口流量再分配因子取为5%[7,23],即假设热组件进口流量比平均值低5%。与之相比,数值计算结果偏于保守。

此外,计算得到了单环路工况下堆芯入口流量分配情况,图10列出了环路入口体积流量为900 m3/h时的计算结果。每组模拟组件位置处均标有堆芯入口流量归一化结果,上、下行数据分别对应表示双环路对称运行与单环路运行工况。与双环路工况下计算结果对比发现：堆芯入口流量分配与双环路工况下明显不同。如上所述,这是由于在2种不同的工况条件下,工质在堆内的流动情况发生了很大改变所致。

表1 121组组件堆芯入口流量分配(双环路工况)Table1 Summary of flow distribution with a ll fuel elements

3.4 敏感性计算研究

针对双环路对称运行工况下不同入口流量(500 m3/h,880 m3/h,900 m3/h)以及多孔介质模型中横向阻力的影响,分别进行了堆芯入口流量分配状况敏感性计算。结果表明这些因素对堆芯入口流量分配的影响较小。其原因缘于在所研究的流量范围工况下,流体始终维持较高雷诺数在堆内流动,主流惯性力占绝对主导地位,因而堆芯入口流量分配基本上与雷诺数大小无关,这与Flanigan等人的实验研究结论相符[2]。

此外,为了考查CFD湍流模型对计算结果的影响程度,选取 RNGk-ε、标准k-ω、SST 3种应用比较广泛的两方程模型进行敏感性计算,相应计算得到了堆芯入口流量分布(环路入口体积流量为900 m3/h工况条件)。对比结果发现,以上湍流模型对计算结果无明显影响(图11)。

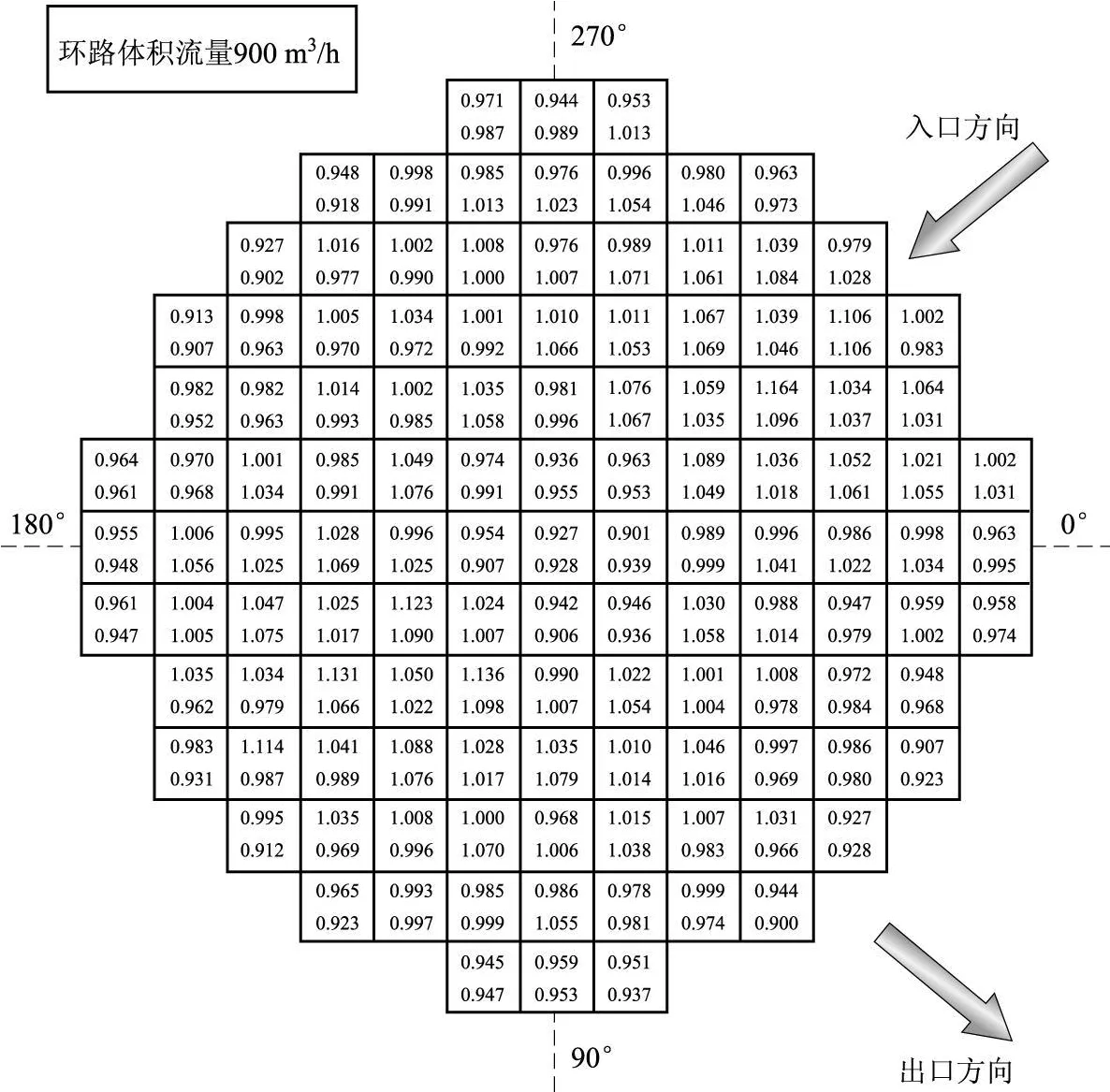
图10 堆芯入口归一化流量分布Fig.10 Comparison of flow distribution factors at core inlet under different loop operation

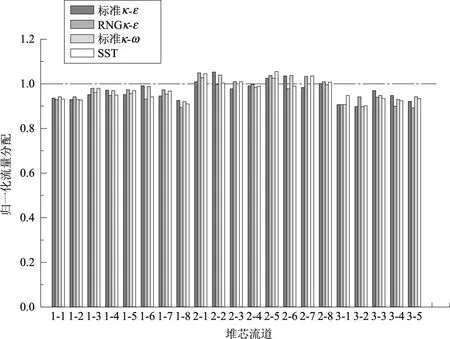
图11 不同湍流模型的堆芯入口归一化流量分布比较Fig.11 Com parison of flow distribution factors at the core in let bymeans o f different turbulencemodels

4 结论

通过计算分析比较可得出以下结论：

(1)应用CFD方法计算得到了600 MW反应堆堆芯入口流量分配结果。分析计算结果表明该方法可行有效。

(2)计算结果表明,双环路对称运行工况下,环路流量的变化对堆芯入口流量分配状况的影响可以忽略。

(3)单环路运行工况下,堆芯入口流量分配与双环路对称运行工况下明显不同,应引起足够关注。

致谢

感谢法国CEA的Marion Chandesris先生给予本文第一作者的探讨和建议。

[1] Bishop A A,Berringer R T.Pressure drop,flow distribution, and m ixing studies for a m odel heterogeneous reactor vessel, YAEC-74[R].Pittsbu rgh, United States：W estinghouse Electric Corporation,1959.

[2] Flanigan L T,W hitacre G R,Hazard H R.Studies of flow and m ixing in a 0.4-scalemodel of the PWR core 2 reactor,BM I-1582[R].Ohio,United States：Battelle Memorial Institute,1962.

[3] HetsroniG.Hyd raulic tests of the San-Onofre reactor m odel,WCAP-3269-8[R].Pittsburgh,United States：W estinghouse E lectric Corporation,1964.

[4] HetsroniG.Use of hydrau licmodels in nuclear reactor design[J].Nuclear Science and Engineering,1967,28：1-11.

[5] 汪利民,宗桂芳,尹涛.600MW 反应堆堆芯入口流量分配实验研究[J].工程热物理学报,1999,20(2)：185-189.

[6] 汪利民,宗桂芳.电站压水堆堆芯水力模拟技术[J].工程热物理学报,2000,21(1)：50-53.

[7] 杨来生,宗桂芳,胡俊.秦山核电二期工程反应堆水力模拟实验研究[J].核动力工程,2003,24(2)：208-211.

[8] Morii T.Hydraulic flow tests of APWR reactor internals for safety analysis[J].Nuclear Engineering and Design,2008,238：469-481.

[9] Radcliff T D,Johnson W S,Parsons J R,et al.V isualization of the low er plenum anomaly in the Westinghouse AP600 reactor[J].Nuc lear Technology,1994,106：100-109.

[10] Yeh H C.M ethod of solving the potential field in complicated geometriesand poten tial flow in the lower p lenum of a p ressu rized water reactor[J].Nuclear Engineering and design,1975,32(1)：85-104.

[11] A lvarez D,Daubert O,Janvier L,et al.Th ree dimensional calculations and experimental investigations of the primary coolant flow in 900 MW PWR vessel[C].Proceedings of NURETH-5,Salt Lake City,USA,[s.n.],1992：586-589.

[12] Frepoli C.Numerical simulation of the inlet plenum flow field for a LWR reactor pressure vessel[J].Applied Mathematics Modeling,1996,20：252-261.

[13] 范静龙,朱丽兵,张明,等.300MW压水堆核电站反应堆下腔室流场数值模拟[C].第十一届全国反应堆结构力学会议论文集,成都,2000：26-30.

[14] Kw on T S,Choi C R,Song C H.Three-dimensional analy sis of flow characteristics on the reactor vessel dow ncomer du ring the late reflood phase of apostu lated LBLOCA[J].Nuclear Engineering and design,2003,226：255-265.

[15] Jeong JH,H an B S.A CFD analy sisof coolant flow in a PWR low er plenum w ithout geom etricalsimplification[C].Proceedings of ICONE-13, Beijing, China,[s.n.],2005.

[16] Höhne T,Sören K.Experim ental and numerical modelling of a buoyancy-d riven flow in a reactor pressu re vessel[C].Proceedings of NURETH-11,Avignon,France,[s.n.],2005.

[17] Fournier Y,Vu rpillot C,Béchaud C.Evaluation of fluid flow in the lower core of a PWR w ith Code_Saturne[J].Nuclear Engineering and Design,2007,237(15-17)：1729-1744.

[18] Jeong JH,Park JP,Han B S.Head Loss coefficient evaluation based on CFD analysis for PWR dow ncomer and lower plenum[J].H eat T ransfer Engineering,2008,29(8)：677-684.

[19] K im MH,Lim H S,Lee WJ.A thermal-fluid assessment of a cooled-vessel concept for a VH TR[J].Nuclear Engineering and Design, 2008, 238：3360-3369.

[20] De Lem os M J S.Turbulence in porous m edia：modeling and ap plications[M].1st edition,UK：Elsevier,2006.

[21] Berringer R,Prevetti G,Tong L S.Lateral flow simu lation in an open lattice core[J].T ransactions of ANS,1961,4(1)：45-46.

[22] Weisman J.C ross flow resistance in rod bundle cores[J].Nuclear Technology,1972,15：465-469.

[23] 李经纬.秦山核电二期工程反应堆热工水力设计[J].核动力工程,1999,20(4)：308-312.