基于多标量模型的感应电机神经网络逆控制

王新

(东南大学 能源与环境学院,江苏 南京 210096)

1 引言

研究具有自适应或鲁棒能力(针对于电机参数变化和负载扰动)的感应电机高性能控制方法非常具有挑战性。近年来,许多专家学者提出了大量的高性能控制方法[1-4],其中,感应电机非线性控制方法[5-8],如基于微分几何理论、逆系统理论及直接反馈线性化方法所实现的解耦及线性化控制,理论上实现了转速(转矩)和磁链之间的大范围解耦和线性化,为提出先进的、实用的控制策略,提供了很好的理论基础,但它们本身严重依赖于数学模型。

提高系统自适应或鲁棒性是反馈线性化方法面临的问题,文献[2,4]提出的自适应反馈线性化理论上严谨,但在只考虑电阻和负载转矩未知的情况下就使结构十分复杂,而且还没有考虑到未建模动态等因素,不易实现工程化。基于电流控制型的神经网络逆控制方法[9]是在忽略电流动态环节的前提下提出的,它增强了系统的鲁棒性,但必须设计高性能的电流调节器。文献[10]基于转子磁场定向(MT)坐标系下的电压控制型感应电机数学模型,采用神经网络逆系统实现了电压分量之间的近似解耦线性化,但它仍然建立在磁场定向准确的基础之上,旋转角的不准势必造成控制性能下降。

感应电机的多标量模型[5,11]是针对两相静止(α β)坐标系下5 阶电机模型变换得到的,它具有状态变量是标量且物理意义明确、不需要旋转坐标变换及模型的输入输出均为直流量等优点,非常适合用于解耦线性化控制器设计。神经网络逆系统方法具有诸多优点[12],并在交流传动系统控制等领域得到成功应用。因此,本文基于多标量模型,利用解析逆系统理论,推导出两种形式的解析逆系统,指出逆系统具有良好的特性。根据神经网络逆系统理论,设计了考虑负载扰动的神经网络逆系统,实现了感应电机系统的自适应解耦线性化,使得外环线性调节器的设计更加简单,进一步提高系统控制性能。最后,对所提结构的有效性进行了仿真验证。

2 感应电机解析逆控制

2.1 感应电机多标量模型

α β坐标系下电压控制型感应电机5阶模型如下:

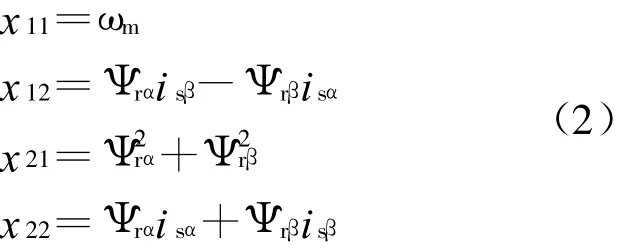
再定义坐标变换 12/α β如下:

考虑式(2)、式(3),感应电机模型式(1)可以写为

定义系统输出为转子机械角速度和转子磁链幅值平方

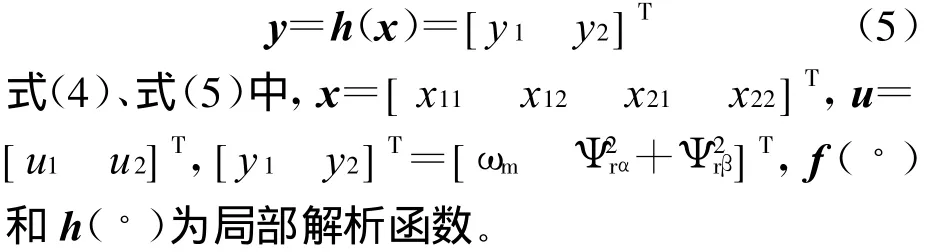
2.2 感应电机解析逆系统

利用解析逆系统理论[12]可知,系统式(4)、式(5)具有向量相对阶{}={2 2},且2+2=4,因此,感应电机系统被完全解耦线性化。根据隐函数定理,可得状态反馈型解析逆系统表达式

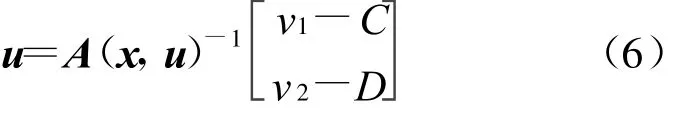
其中

根据文献[13]中的方法,得到输入积分型的

式(7)可以简化为

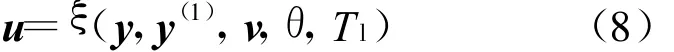
通过对解析逆系统进行分析,这种解析逆系统具有存在两种形式解析逆系统、输入积分型逆系统可以补偿负载转矩且与原系统构成的复合系统不含零动态等优点,这些使设计优良的神经网络逆系统成为可能。

3 感应电机神经网络逆控制

式(6)和式(7)是两种形式的解析逆系统,当参数变化和负载扰动时,它们都具有参数敏感性,解耦线性化会被破坏,系统性能难以进一步提高。为此,本节设计神经网络逆系统(即采用神经网络逼近逆系统的静态表达式,利用积分器实现逆系统动态特性),它可实现含有不确定性因素感应电机系统的自适应解耦线性化,得到的2个二阶积分子系统不含变化的感应电机参数,使得外环控制器设计更加方便。

3.1 神经网络逆系统设计

采用解析逆系统控制(ANISC)结构来采集用于神经网络训练的数据,输入输出数据根据式(8)确定,转子磁链通过观测或计算得到,负载转矩假定可测,神经网络逆系统的具体设计步骤如下。

1)激励信号选择。在带磁链观测的感应电机解析逆系统控制结构中,取转速和转子磁链幅值平方给定为一定范围内幅值随机变化且变化周期恒定的信号。为了避免求导时导数过大,采用二阶Butterworth低通滤波器对给定信号进行滤波。

3)神经网络训练和测试。把训练数据分为两组,一组用于训练,一组用于测试;选用3层前馈BP神经网络,采用试凑法来确定隐层神经元的个数。选用LM算法对神经网络进行训练,训练好的神经网络再经过测试检验来确定是否适合使用。

3.2 神经网络逆控制结构(NNIC)

设计好的神经网络逆系统可以实现含有不确定性因素感应电机系统的自适应解耦线性化,得到的转速和转子磁链幅值平方子系统均为1/s2,因此,可以采用PD调节器进行调节,利用线性系统理论设计PD调节器,最终完成神经网络逆复合控制器设计,得到基于多标量模型的感应电机NNIC结构如图1所示。

图1 感应电机NNIC结构原理图Fig.1 T he diag ram for NNIC for IM

根据图1,再考虑到实际情况,感应电机NNIC的实现结构如图2所示,图2中,定子电流和直流母线电压可以通过电流和电压霍耳传感器测量得到,定子ab相电流用来观测转子磁链,直流母线电压用来调制逆变桥开关管所需要的PWM信号。转速通过光电编码器测量得到通过测量得到。神经网络逆系统模块用来产生参考信号,再通过 变换环 节 α β/12 得到神经网络逆系统输入通过PD调节器调节得到。

图2 感应电机NNIC的实现结构Fig.2 T he implement structure of NNIC for IM

所提结构有如下特点。

1)与基于α β坐标系下电压控制型感应电机的NNIC相比,其对应的解析逆系统有两种形式,输入积分型结构使得负载转矩更加容易补偿,神经网络以逼近定子电压直流分量代替了交流分量,这使得神经网络逆系统设计简便、性能优良。

2)与基于α β坐标系下电流控制型感应电机的NNIC相比,由于通过神经网络逆系统取代了更加复杂的物理关系,省略了电流控制环节,所提结构更简单。

3)与基于MT坐标系下的感应电机NNIC相比,磁链观测不准(进一步为旋转角)对控制性能所带来的影响更小。

4 系统仿真

采用Matlab/Simulink建立感应电机逆控制(包括解析逆和神经网络逆)系统的仿真模型,采用的笼式感应电机参数为:额定功率1.1 kW,额定转速146.6 rad/s,极对数=2,定子电感=0.574 H,转子电感=0.580 H,互感=0.55 H,转子惯量J=0.002 1 kg◦m2,定子电阻Rs=5.9 Ω,转子电阻=5.6 Ω。转速和转子磁链PD调节器的参数相同,分别为==1 300和KDω=KDΨ=65,这里下标 ω,Ψ分别为转速和转子磁链幅值平方调节器的控制参数。下面分两种情况进行仿真对比研究。

4.1 参数不变时

假定感应电机参数不变,对ANIC和NNIC两种方法进行仿真。设转速给定为:初始值80 rad/s,在1s处突变为140 rad/s;转子磁链幅值平方为:初始值1.0 Wb2,在3 s处突变为0.5 Wb2;负载转矩为:空载启动,在2 s处突变为3N◦m。采用截止频率为30rad/s的二阶Butterworth低通滤波器对给定信号进行滤波,仿真时间为4 s,比较结果如图3所示。仿真结果表明,当感应电机参数不变时,ANIC实现了完全解耦线性化,但负载突变时,转速所受影响较大;NNIC实现了近似解耦线性化,当负载转矩突变时,转速所受影响比ANIC时要小,这是因为NNIC对负载转矩进行了补偿。

图3 参数不变时,ANIC和NNIC仿真结果比较Fig.3 T he comparison simulation results of ANIC and NNIC when the parameters are constant

4.2 参数变化时

感应电机在实际运行过程中温度升高,定转子电阻会增大,假定和分别变为8 Ω和10 Ω,其他运行参数与4.1节相同,仿真结果如图4所示。仿真结果表明,NNIC的转速响应所受影响很小,具有高动、静态性能;ANIC的转速响应速度变慢,当加上负载时,ANIC的转速下降,因此,当扰动存在时,参数变化对ANIC影响加大,破坏了ANIC的解耦,并使控制性能受到严重影响。两种控制结构的转子磁链幅值平方响应都受到了影响,与ANIC相比,NNIC所受影响很小。因此,NNIC比ANIC具有更强的鲁棒性,从仿真结果可以得出:当转子参数变化和负载扰动存在时,NNIC实现了感应电机的近似解耦及线性化,使得系统具有很高的控制性能。

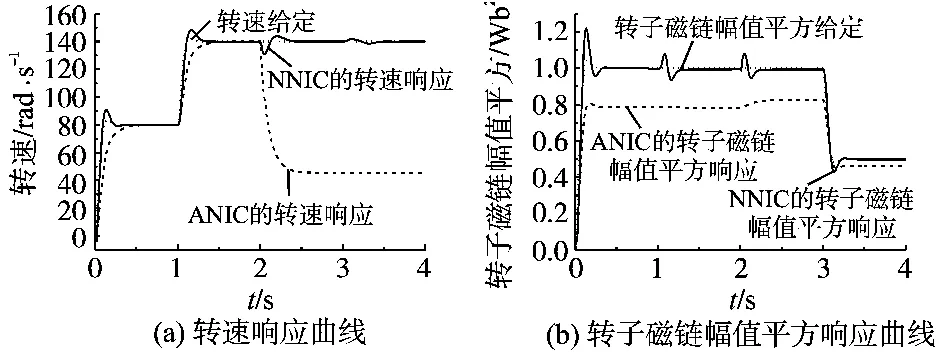
图4 参数变化时,ANIC和NNIC仿真结果比较Fig.4 The comparison simulation results of ANIC and NNIC when the parameters varying

5 实现方案

5.1 系统实验平台[14]

实验平台结构如图5所示,主要包括德国dSPACE公司的半实物实时仿真工具DS1103及连接面板CLP1103、自行研制的接口板、感应电机及工控机。接口板上包括三菱公司的ASIPM(PS12036)、整流器和逆变器之间的直流电路控制部分及电压电流霍耳传感器。工控机通过16位ISA总线与DS1103板进行高速数据交换,电机转速、直流母线电压、定子电流分别通过光电编码器和电压电流传感器测得,并通过连接面板CLP1103与 DS1103板的相关单元连接。DS1103板的微处理器根据控制算法运算得到的控制信号通过 TMS320F240以PWM信号的形式送到接口板上的ASIPM,从而实现对感应电机的变压变频控制。如果ASIPM出现故障,ASIPM的故障信号反馈给DS1103板的中断端,关闭控制信号,从而使系统得到保护。

图5 实验平台结构框图Fig.5 The structure frame for experiment platform

5.2 软件实现方案

实验平台的软件部分由Matlab/Simulink和dSPACE提供的 RTI模块和ControlDesk组成。首先采用直接转子磁场定向控制结构[1]采集训练所需实验数据,将训练数据进行处理后用于训练神经网络。然后,实现所提控制系统结构,其中控制系统算法(见图2中的虚线部分)采用Matlab/Simulink 实现 ,其中坐标变化 α β/12,α β/abc和转子磁链观测器(采用电流转速型)通过搭建模块的方式实现;神经网络逆系统中的神经网络由训练时Matlab自动产生的神经网络模块实现;PD调节器及其他相关环节通过软件提供的模块实现。RTI模块是连接软件和硬件接口电路的工具,两相定子电流和直流母线电压采集软件通过DS1103ADC_17,DS1103ADC_18和DS1103ADC_19接口模块实现,转速通过DS1103ENC_SETUP和DS1103ENC_POSC1模块实现,负载转矩采集通过DS1103ADC_20模块实现,为了消除相关物理量中的谐波,采用适当点数的滑动平均滤波器进行滤波。PWM波形的产生通过 DS1103SL_DSP_PWMSV模块实现。ControlDesk用于实验物理量的采集、显示和状态控制,同时可以方便地进行调节器参数的在线修改。

6 结论

为了解决具有不确定性因素的感应电机系统控制问题,本文基于感应电机多标量模型,提出了基于多标量模型的NNIC结构。此结构与其他NNIC相比具有诸多优点,并对系统的软、硬件实现方案进行了讨论。仿真对比结果分析表明,当参数变化和负载转矩扰动时,NNIC基本实现了感应电机系统的自适应解耦线性化,具有较高的动、静态控制性能。

[1] (美)比马尔 K博斯.现代电力电子学与交流传动[M].北京:机械工业出版社,2004.

[2] M arino R,Peresada S,Tomei P.Global Adaptive Output Feedback Control of Induction Motors with Uncertain Rotor Resistance[J].IEEE Trans.Autom.Control,1999,44(5):967-983.

[3] Boukas T K,Habetler T G.High-performance Induction Motor Speed Control Using Exact Feedback Linearization with State and State Derivative Feedback[J].IEEE T rans.Power Electron.,2004,19(4):1022-1028.

[4] Mohamed Rashed,Peter F A MacConnell,Fraser Stronach A.Nonlinear Adaptive State-feedback Speed Control of a Voltage-fed Induction Motor with Varying Parameters[J].IEEE T rans.Ind.Appl.,2006,42(3):723-732.

[5] Kazmierkowski M P,Krishnan R,Blaabjerg F.Control in Power Electronics Selected Problems[M].San Diego:Academic Press,2002.

[6] 刘国海,戴先中.感应电动机调速系统的解耦控制[J].电工技术学报,2001,16(5):30-34.

[7] 李擎,杨立永,李正熙,等.异步电动机定子磁链与电磁转矩的逆系统解耦控制方法[J].中国电机工程学报,2006,26(6):146-150.

[8] 张春朋,林飞,宋文超,等.基于直接反馈线性化的异步电动机非线性控制[J].中国电机工程学报,2003,23(2):99-102.

[9] 王新,戴先中.一种基于神经网络逆的感应电动机解耦线性化改进策略[J].电工技术学报,2008,23(4):32-38.

[10]戴先中,张兴华,刘国海,等.感应电机的神经网络逆系统线性化解耦控制[J].中国电机工程学报,2004,24(1):112-117.

[11]Krezminski Z.Nonlinear Control of Induction Motor[C]∥Proceedings of 10th IFAC World Congress,Munich,Germany,1987:349-354.

[12]戴先中.多变量非线性系统的神经网络逆控制方法[M].北京:科学出版社,2006.

[13]张兴华.感应电机的神经网络逆系统解耦线性化控制[D].南京:东南大学,2002.

[14]王新,戴先中.同步旋转坐标系下感应电机神经网络逆控制[J].电气传动,2008,38(5):52-57.

修改稿日期:2010-05-11