基于场分布的平面散乱点集B样条曲线重建算法
2010-04-26黄童心王文珂宋征轩
黄童心, 王文珂, 张 慧, 宋征轩
(1. 清华大学软件学院,北京 100084;2. 清华大学计算机科学与技术系,北京 100084;3. 信息系统安全教育部重点实验室,北京 100084;4. 清华信息科学与技术国家实验室,北京 100084)
基于场分布的平面散乱点集B样条曲线重建算法
黄童心1,3,4, 王文珂1,2,3,4, 张 慧1,3,4, 宋征轩1,3,4
(1. 清华大学软件学院,北京 100084;2. 清华大学计算机科学与技术系,北京 100084;3. 信息系统安全教育部重点实验室,北京 100084;4. 清华信息科学与技术国家实验室,北京 100084)
平面散乱点集的曲线重建是逆向工程研究的核心问题之一。该文在Goshtasby算法的基础上,提出了一种基于场分布的平面散乱点集B样条曲线重建算法。首先,通过估计场强基函数的边界提高量子化效率,生成散乱点集场分布的数字图像;然后,利用图像细化结合改进的BFS(Breadth-First-Search)算法来避免数字图像中由于存在大量冗余分支像素而难以生成脊轮廓的问题;最后,采用加权最小二乘法延长重建曲线,改进Goshtasby算法所得的开曲线在端点处收缩的缺点。实验表明,对于带噪声的平面稠密点集,该算法可有效地重建反映点集形状和走向的B样条曲线。
计算机应用;B样条曲线重建;场分布;散乱点集
由平面采样点集重建曲线是逆向工程几何造型领域中的一个重要问题[1-3]。根据采样数据点集的性质可将曲线重建方法分为有序离散点集的曲线拟合和无序散乱点集的曲线拟合。对于前者而言,曲线重建效果往往受到数据点集参数化方法的影响,其代表有均匀参数化、弦长参数化和向心参数化[4-7]等。在逆向工程领域获取的测量数据一般是大规模的无序散乱点,有噪声且采样密度较为稠密,难以直接进行曲线拟合,往往需要首先进行定序[1-2]。特别地,当数据点集反映的几何拓扑结构较为复杂时,仅仅将其拟合成一条单独的曲线是不合适的,应按其结构特征分别以各条连续的光滑曲线来表示。
目前无序散乱点集曲线重建的典型方法有如下几类:Levin、Lee的移动最小二乘法(MLS)[2,8],Pottmann的图像细化法[3],Fang的弹力模型法[9]和Taubin的隐式单纯模型法[10],Amenta的基于Voronoi图Crust算法的β骨架法[11]等。其中,移动最小二乘法需要对数据点集进行两次局部最小二乘回归,计算量较大;图像细化法的准确性受点集投影的网格分辨率的直接影响,重建效果较为粗糙;模型法依赖于给定优化模型的目标函数,往往需要进行迭代求解,对于数据点集中的噪声较为敏感;骨架法则不适用于稠密点集,而且抗噪性不够理想。国内也有学者提出了平面无序点集曲线重建的跟踪算法[12]和场表示算法[13],避免了上述方法的某些弊端,文献[12]成功模拟连续曲线的跟踪过程并引入质量控制机制解决了简单光滑曲线的重建问题;而文献[13]则沿着构造场函数的梯度方向运动以其极限位置为重建曲线。Lin的基于区间B样条[14]的曲线重建方法则可以有效过滤噪声,以及处理不均匀的采样点集。
由于点集形状千差万别,上述曲线重建方法的适用范围各不相同,但是它们均难以实现对稠密、带噪声的散乱点集进行有效区域划分以重建出多条曲线。文献[1]通过模拟散乱数据点集中各个数据点形成空间场分布的物理现象,有效解决了该问题,但是还存在如下不足之处:量子化生成表示散乱点集场分布的数字图像时运算效率低下;数字图像中含有大量冗余分支像素使得脊轮廓生成困难;以及重建曲线不能很好反映点集端点处的形状特征。本文在文献[1]算法的基础上针对这些不足进行了改进,并给出实例证明了本文算法的有效性。
1 相关工作
假设给定平面散乱数据点集S = { pi= (xi, yi) | i = 1, …, N },其中pi表示点集S中的第i个数据点,N表示S中数据点的个数(如图1所示),作者的目标就是根据数据点集的特征拟合出一条或多条反映该点集形状和走向的B样条曲线。文献[1]首先利用图像梯度跟踪散乱数据点集形成场分布的局部极大值点在平面的投影获取点集的脊线(即曲线的初始逼近),然后借助脊线将原始数据点集划分成多个子集,以及对各个子集的数据点进行排序,最后采用传统的曲线拟合方法对已定序的数据点重建出相应的曲线。
文献[1]假设散乱数据点集 S中各个数据点pi都具有以其为中心的单调递减线性场,并且该点在平面内任意一点p(x, y)处的场强度由式(1)所示的逆多元二次(inverse multiquadric)径向基函数所定义[15]

式(1)的几何意义是数据点 pi到平面内任意一点p的反向距离,即两点间欧氏距离的倒数,其中参数r是某个大于0的常量以避免被0除。不难看出,数据点pi在点p处的场强度会随着p到pi距离越远而越小。而散乱数据点集S在平面内任意一点p处的场强度则是点集中各个数据点pi在该点的场作用之和,由式(2)所示的场表面(field surface)函数表示

场表面函数 g的局部极大值点构成了其脊线,跟踪场表面函数g的局部极大值点在xy平面的投影,就可获取曲线的初始逼近。实验证明参数r还可作为获取脊轮廓的平滑度调整因子。一般而言,随着参数r的增大,对应的场表面越趋于平滑,因此获取脊轮廓也就越平滑。当r取值为5时,可获得一个较理想的平滑度。同时,注意到直接通过解析式方法求解函数g的局部极大值点是相当困难的,因此文献[1]给出了以下的重建算法基本步骤:
步骤1量子化生成表示散乱数据点集场分布的数字图像(digital image),即将场表面g转化成数字图像。这里的图像指的是一个二维数组,它的各个元素也称为像素,是通过对显式函数z = g(x, y)在xy平面上沿着x和y轴方向进行等间隔划分采样得到的对应像素强度值(如图2所示)。数字图像的分辨率则定义为像素的总数目。
步骤 2找到数字图像中的次要脊(minor ridge)像素和主要脊(major ridge)像素,并且依据分支(branch)像素将这些次要脊像素划分成各个次要脊线段(minor-ridge segment)。其中几个重要概念的定义如下:
次要脊像素 其强度值高于它的两个邻接像素的强度值且这两个邻接像素在彼此相反的两个方向上,即满足式(3)所示的4个条件之一的像素便可被称为次要脊,其中I(i, j)表示i行j列像素的强度值

主要脊像素 其强度值高于它在梯度方向(gradient direction,即强度值改变最大方向)上的邻接像素的强度值。
次要脊线段 次要脊像素的连通集合,其中各个像素至多有两个邻接次要脊像素。
分支像素 两条以上次要脊线段的公共端点,即它至少有3个邻接次要脊像素。
步骤 3移除不含主要脊像素的次要脊线段,找出剩余的次要脊线段所形成的脊轮廓(ridge contour)。根据上述定义,主要脊是次要脊的子集,而且主要脊的像素点一般不会落在较小的、有噪声的次要脊线段上(或称为旁支),而是落在代表了原始数据点集脊线的轮廓上。脊轮廓就是由次要脊线段连接而成的集合,其中各个次要脊线段至少含有一个主要脊像素。
步骤4利用脊轮廓将原始数据点集划分为多个子集,并通过跟踪各个子集的数据点在对应脊轮廓上的投影对它们进行排序。
步骤5对于各个子集已排序的数据点,应用现有的方法,如Piegl和Tiller在文献[16]中介绍的B样条拟合有序离散数据点集的方法,得到重建的B样条曲线。

图1 平面散乱数据点集

图2 表示散乱数据点集场分布的数字图像
文献[1]提出的基于散乱数据点集场分布的曲线重建方法可基于数据点集的物理特征自动完成对点集的区域划分,因此适用于多条曲线的拟合,但是也存在如下问题限制了其实用性:
(1) 在步骤1中,若数字图像的采样分辨率较高,或者原始数据点集中数据点的个数较多,则量子化生成数字图像时运算效率低下。
(2) 在步骤 2 、3中,数字图像往往含有大量冗余分支像素,不利于生成形体较佳的脊轮廓,进而影响后期散乱点的排序效果。
(3) 在步骤4中,对于开点集,由于点集端点附近的主要脊像素分布较少,根据步骤3,大部分端点处的脊像素都应作为旁支而被删除,导致获取的脊轮廓在点集端点处收缩,因此重建出的开曲线不能很好地反映点集端点的形状。
2 本文算法
针对上述文献[1]算法的不足,本文作了以下改进:首先,通过估计场强基函数的边界,即各个数据点的场作用范围,减少了大量冗余运算从而提高了量子化生成数字图像的效率;其次,在不改变图像分辨率的前提下,采用图像细化结合改进的BFS算法解决了脊轮廓生成困难的问题;最后,利用加权最小二乘法对开点集端点附近因脊轮廓缩短而无法有效投影到脊轮廓上的数据点进行排序,进而延长了重建曲线的端点,改善了开曲线的重建效果。
2.1 估计场函数边界提高量子化效率
量子化生成数字图像时,一般首先将散乱数据点集的最小包围盒沿着 x y平面坐标轴方向按栅格尺寸λ进行等间隔划分,其中每个栅格就代表了数字图像中的一个像素,栅格尺寸λ则决定了数字图像的分辨率;然后取数字图像中各个栅格的中心点为采样点,分别代入式(2)定义的场表面函数g中计算出该栅格代表像素的场强度。为了确保原始数据点集中绝大部分数据点都映射到数字图像唯一的栅格单元中,栅格尺寸λ应根据点集分布均匀性进行设置,一般取点集分布密度ρ的k倍。点集分布密度ρ可由下列方法估计得到[17]:在原始数据点集中随机取 m个数据点pi,计算离点pi最近点的距离di,则分布密度为,m一般取20~30。于是栅格尺寸

设散乱数据点集中最大、最小 x 、y坐标分别为 xmax、ymax、xmin、ymin,同时为避免散乱点位于包围盒外,给定容差ε放大包围盒,则沿着x、y坐标轴方向划分的栅格数分别为其中符号表示向上取整。栅格总数a*b即为数字图像的分辨率。为计算简便,也可以令分辨率的高和宽a=b=512。根据式(2),要得到数字图像中一个像素的场强度,需要计算数据点集中的所有数据点到该像素的反向距离,若点集中数据点的个数为N,则每个像素需要计算N次反向距离,于是总的计算次数为a*b*N。量子化运算时间会随着原始数据点集中数据点的个数或者数字图像分辨率的增加而迅速增加,而点云数据通常规模较大,这样庞大的计算量是不可接受的。
本文通过估计场强基函数的边界减少大量冗余运算,进而提高了量子化生成数字图像的效率,其重要依据在于散乱数据点集中各个数据点的场辐射范围是有限的,可以近似认为其作用范围为距离该数据点半径为R(以像素为单位)的圆形域内,而圆形域外部的场强度几乎衰减为0(如图3所示)。只要圆形域半径R足够大,使得其外部的场强度I(R)小于一定的阈值δ,便可忽略圆形域外部区域场强度的计算,并且不会影响数字图像的生成效果,实验证明δ可取0.01。因此,对于每个数据点,只需计算以其为中心的圆形域范围内πR2个像素的场强度,此时总的计算次数为πR2*N。当R<<a或者R<<b时,可大幅度提高计算速度。由于R是通过估计场强基函数边界得到的某个常量,于是量子化生成数字图像的时间复杂度约为O(N)。

图3 数据点的场辐射范围
式(1)所示的逆多元二次径向基函数可转化成一元函数[R2+r2]-1/2的形式,其中表示欧几里德(Euclidean)范数。由于该一元函数表示的场强值I(R) = [R2+r2]-1/2是关于半径R的单调递减函数,当参数r取经验值5时,令I(R)小于阈值 δ = 0.01,可计算得到 R 的最小值为100,则散乱数据点的反向距离场强值可表示为如式(4)所示分段的形式

如果数字图像分辨率为512*512,则对于逆多元二次径向基函数,通过估计场强基函数边界可以将生成数字图像的运算效率提高一个量级。径向基函数实际上是利用一个一元函数作用在欧几里德距离上,然后做平移,因此具有物理上各向同性的性质,适用于模拟数据点的场分布。于是也可以选择其他衰减速度更快的径向基函数,如高斯基函数、紧支柱正定基函数[18]等来模拟数据点形成的场,从而更加高效地实现数字图像的量子化。以高斯基函数为例,其定义如式(5)所示当式中参数σ仍取经验值5,且该式表示的场强值小于阈值δ = 0.01时,可计算得到R的最小值为11。仍然取分辨率为512*512,则采用高斯径向基函数时,运算时间约是原始数字图像量子化方法的πR2/ (512*512) ≈ 1/690,大幅提高了生成数字图像的效率。

2.2 图像细化结合改进BFS算法去除旁支
图1所示的散乱点集经量子化后,生成的数字图像如图4所示:图中左侧表示的是根据式(3)定义找到的数字图像中的次要脊像素,它们实际上就是使得场表面函数g具有局部极大值的那些像素点;右侧表示的是指定局部像素区域内各种类型的像素排列情况的放大示意,其中方形标记表示主要脊像素、半径较大的圆形标记表示次要脊像素、半径较小的圆形标记表示分支像素。
图4表明,初始的数字图像不仅含有大量冗余分支像素,而且其次要脊像素排列情况具有明显的不规则性,还带有一些噪声脊像素,难以生成用于散乱数据点集区域划分以及各子集数据点排序的脊轮廓。本文采用图像细化结合改进的BFS算法解决这一问题:首先,利用图像细化算法对数字图像进行初步细化,抽取出只有一个像素宽度的图像骨架,以此大幅减少冗余分支像素;然后,通过广度优先遍历(BFS)数字图像中的所有次要脊像素,将数字图像转化为广度优先生成森林;最后,对生成森林中各棵生成树进行剪支运算,去除不含主要脊像素的次要脊线段(即旁支)以获取所需的脊轮廓。

图4 数字图像中各种类型的像素
(1) 利用图像细化初步细化
一般说来,栅格尺寸λ的设定对于生成数字图像的质量和精度有直接影响,尺寸越小数字图像越精细,反之则越粗糙。在实际应用中,为保证重建曲线的精度,有必要适当减小栅格尺寸以增大数字图像的分辨率,然而实验证明较高的图像分辨率往往会形成大量的冗余分支像素(如图4所示)。这些冗余分支像素也满足至少含有 3个邻接次要脊像素的基本条件,但是不同于作为两条以上次要脊线段公共端点的正常分支像素,它们是由于许多次要脊像素并列排列,从而导致超出一个像素的线条宽度所造成的,因此并不能作为将数字图像中次要脊像素划分成各个次要脊线段的依据。作者考虑采用图像细化算法对数字图像进行初步细化,提取出数字图像的线形骨架以剔除冗余分支像素。
图像细化算法种类较多,代表性的有Hilditch细化算法[19]、Pavlidis细化算法[20]、Rosenfeld细化算法[21]、索引表细化算法[22]等。细化算法一般遵循以下准则:图像骨架必须保持原图像的连通性和拓扑结构;图像骨架尽可能是原图像的中心线;细化的结果应是一个像素宽度的线条图像,即非特殊点(交点和端点)在8连通意义下只有两个邻接像素等。根据数字图像中次要脊像素排列特征的不同可以选择其中任意一种算法进行初步细化,本文采用了文献[22]介绍的索引表细化算法。
本文采用的索引表细化算法是在应用上述细化准则的基础上,依据次要脊像素p的8个邻接像素是否也为次要脊像素,构造一张包含256种情况的剔除表,水平、竖直方向交替扫描数字图像中各行各列的次要脊像素,通过查表即可判断该次要脊像素是否应该被剔除。以次要脊像素为中心像素的3*3的像素模板为例,若该次要脊像素为内部点、直线端点,或除去后增加连通分量则不能被删除。图5给出了次要脊像素p八邻域情况的几个示例:(a)中心像素点为一个内部点,不能被删除,否则骨架被掏空;同样道理,(b)中心像素点也不能被删除;(c)中心像素点不是骨架,可以被删除;(d)中心像素点不能被删除,否则破坏图像的连通性;(e)中心像素点也不是骨架,可以被删除;(f)中心像素点为直线的端点,不能被删除,否则整条直线都将被删除;(g)中心像素点为孤立点,一般作为噪声可以被删除。利用索引表细化算法初步细化后,获得了理想的结果,无论是冗余分支像素,还是数字图像中的噪声都大大减少了(如图 6 所示)。不妨设数字图像中的像素总数为n,图像中包含的次要脊像素个数为 m,则该细化算法时间复杂度约为O(nlogm)。

图5 次要脊像素八邻域情况

图6 初步细化后的数字图像
(2) 利用BFS生成森林去除旁支
通过上面的步骤,大量冗余分支像素已被剔除,接下来可采用迭代的方式去除数字图像中的次要脊旁支。旁支又可分为普通分支(branches)和环(loops)两种类型。普通分支的一个端点是分支像素,另一个端点则是只有一个邻接像素的次要脊像素,因此它是开的。与此相反,环则是封闭的,它只有分支像素作为其端点,如图6右侧的局部放大示意所示。为了有效识别这两种类型的旁支,并且统一处理次要脊像素排列的各种复杂情况,本文采用了改进的BFS算法。
改进的 BFS算法基本思想是通过广度优先遍历数字图像中的所有次要脊像素,将数字图像转化为多棵以次要脊像素为结点、相邻次要脊像素的邻接关系为边的广度优先生成树所构成的广度优先生成森林。具体转化方式如下:逐行逐列扫描数字图像中的像素,若遇到第一个未被访问的次要脊像素 s ,就将其作为初始结点(生成树的根)插入到搜索队列中,然后依次移出队首结点u,并将队首结点u所有未访问过的邻接次要脊像素v加入搜索队列,同时将v作为新结点、邻接关系(u, v)作为新边插入到本次循环创建的生成树中,直到队列为空循环搜索过程才结束。一方面,由于生成森林具有不含环(或称回路)的特性,因此环类型的旁支在计算得到生成森林后也被转化为普通分支类型,有利于对这两种类型的旁支进行统一处理;另一方面,由于非连通的生成森林是由多棵连通的生成树所构成,每棵生成树就代表了数字图像中次要脊像素形成的一个连通分量,因此在将数字图像转化为生成森林后,实际上就完成了对数字图像中的次要脊像素的分块工作,有助于后期根据点集的拓扑结构特征生成多条脊轮廓,以及顺利解决点集的区域划分问题。将数字图像转化为生成森林的算法描述如下:
输入细化后的数字图像I
输出以次要脊像素为结点、相邻次要脊像素的邻接关系为边的广度优先生成森林Gπ
GENERATE-BFS-FOREST(I )
for each pixel p of image I // 逐行逐列扫描数字图像I中的像素p
do if p is minor ridge // 如果p为次要脊像素,初始化p的访问标记为WHITE,即未访问
then color[p]←WHITE
create a BFS forest Gπ// 创建广度优先生成森林Gπ
for each pixel s of image I // 逐行逐列扫描数字图像I中的像素s
do if s is minor ridge and color[s]=WHITE // 如果s是次要脊像素且未被访问
then create a BFS tree T // 创建一棵广度优先生成树T
color[s]←BLACK // 设置 s 的访问标记为BLACK,表示已被访问
insert pixel s as a vertex into the tree T // 将像素s作为结点插入生成树T中
root[T ]←s // 以初始结点s作为生成树T的根
Q←Ф // 初始化队列Q为空
ENQUEUE(Q,s) // 将像素s插入Q队尾
while Q≠Ф // 若队列Q非空,则执行while循环;否则,不执行
do u←DEQUEUE(Q) // 移出Q队首u
for each v in u’s eight adjoint pixels // 逐个查找u的8个邻接像素v
do if v is minor ridge and color[v]=WHITE // 如果v是次要脊像素且未被访问
then color[v]←BLACK // 设置v的访问标记为BLACK
insert pixel v as a vertex into the tree T // 将像素v作为结点插入生成树T中
insert edge(u, v) into the tree T // 将(u, v)作为边添加进生成树T中
ENQUEUE(Q, v) // 将像素v插入Q队尾
add tree T to the forest Gπ// 将本次循环得到的生成树T添加到生成森林Gπ中
return Gπ// 返回生成森林Gπ
当数字图像中所有的次要脊像素被访问并作为结点插入生成森林的各棵生成树后,建生成森林的过程结束。由于设置了访问标记,因此保证了每个次要脊像素至多只有一次入队和出队。入队和出队操作需要O(1)的时间,则队列操作所需的全部时间为 O(m)。而只有当每个次要脊像素出队时,才会查找其8个邻接像素,故查找邻接像素花费时间也为 O(m)。此外,由于初始化及建生成森林均需遍历一次数字图像,相应的时间复杂度为O(n)。于是,建生成森林总的运行时间为O(m+n),通常m<<n。
建完生成森林,接下来需要对生成森林的各棵生成树进行剪支运算。从叶子结点开始向树根方向搜索,记录搜索路径path上经过的各个次要脊像素并设置访问标记,如果在path路径上遇到第一个分支像素,或者通过path路径无法找到新的未访问的结点,则此次搜索结束。然后根据此次搜索的path路径上是否含有主要脊像素,判断是否应将该路径上的像素作为旁支而从生成树中予以摘除。对于每棵生成树,剪支算法描述如下:
输入 生成森林中各棵生成树 T=(V,E),其中 V是T中结点的集合,E是T中边的集合
输出 无
REMOVE-BRANCHES(T )
for each vertex p∈V [T ] // 逐个遍历生成树T中的结点p,初始化p的访问标记为WHITE
do color[p]←WHITE
for each vertex u∈V [T ] // 逐个遍历生成树T中的结点u
do if u is a leaf and color[u]=WHITE // 如果u是叶子结点(即度为1,此处度表示邻接边数)且未被访问
then make a path // 开始记录搜索路径path
repeat
color[u]←BLACK // 设置 u的访问标记为BLACK
add u to the path // 将u添加到搜索路径path中
for each edge(u,v)∈E[T ] // 逐条查找生成树T的边(u,v)
do if color[v]=WHITE and v is not branch // 如果边的另一个端点v未被访问且不是分支像素
then u←v // 更新u为v,跳出for循环
break
until color[u]=BLACK // 若找到新结点u,则继续执行repeat循环;否则,不执行
if path is not empty and doesn’t contain major ridge // 如果搜索路径path非空且不存在主要脊像素
then remove vertexes of path from the tree T // 将path路径上的像素从生成树T中删除
return
剪支运算中,若令生成树中的结点数为V,边数为E,则初始化和寻找叶结点的运行时间为O(V ),搜索路径的运行时间为O(E),总的时间复杂度为O(V+E)。由于结点数V也表示生成树代表的数字图像中某个连通分量所包含次要脊像素的个数,因此V一般远小于数字图像中的像素个数n,并且对树形结构而言,边数E = V-1,则O(V+E ) = O(2V-1) = O(V )。由于非连通的生成森林是由多棵连通的生成树所构成,因此生成森林中的结点个数就为数字图像中次要脊像素的个数m,则所有生成树的剪支运算时间复杂度应为 O(m),可见剪支运算的开销是较低的。综上所述,BFS算法去除旁支总的时间复杂度为O(m+n)+ O(m)=O(m+n)。本文利用图像细化结合改进的 BFS算法去除旁支后得到了形体较好的脊轮廓(如图7所示)。

图7 去除旁支后生成的脊轮廓
对于几何拓扑结构较为复杂的多连通数据点集,通过上述改进的BFS算法可获得多棵代表该点集拓扑结构的生成树,经剪支运算后生成多条对应的脊轮廓。这些脊轮廓被用于对散乱数据点集进行区域划分以及各个子集的数据点排序:首先,将原始数据点集中的每个数据点pi赋给离它最近的一条脊轮廓,以此将点集划分为各个子集;然后,确定各子集的数据点到代表该子集的脊轮廓中的最近像素(或称之为投影);最后,跟踪轮廓上的脊像素,以投影像素被访问的顺序对散乱点进行排序。
2.3 加权最小二乘法延长重建曲线
将平面无序散乱点集转化为各个有序的离散点子集后,就可采用文献[1]介绍的参数化方法和Piegl和Tiller在文献[16]中介绍的B样条最小二乘逼近方法将每个离散点子集拟合成满足一定拟合误差限制的B样条曲线。
由于分布在开点集端点附近的主要脊像素数目较少,因此根据Goshtasby曲线重建方法的步骤3,大部分端点处的脊像素都应作为旁支而被删除,从而导致生成的脊轮廓在点集端点处收缩,因此重建出的开曲线无法很好地反映点集端点处的形状(如图8所示)。

图8 开点集重建曲线端点处收缩
对开点集进行曲线重建时,缩短的脊轮廓会使得点集端点附近沿着脊轮廓的延长线方向上的散乱点都投影到脊轮廓的端点(像素)上,因此,仅通过跟踪脊轮廓上的投影无法对点集端点附近的数据点进行有效排序,进而造成重建出的开曲线在端点处缩短。由于在对散乱数据点集进行区域划分时,已经计算过散乱数据点集的各个数据点到相应脊轮廓的投影,可找出投影到脊轮廓端点的数据点形成的端点邻域点集,并对其进行局部拟合得到一条局部回归线,通过对端点邻域点集中的数据点到该局部回归线的投影对其进行排序,进而延长重建曲线的端点。记脊轮廓端点为p*,投影到p*的某个邻域范围内的数据点pj(xj, yj)构成的点集为A,同时不妨设A中数据点的个数为k,显然A⊆S且k<<N。考虑先采用加权最小二乘法(WLS)对端点邻域点集A中的所有数据点拟合出一条关于点p*的局部回归线L*:y = ax + b,即极小化式(6)所示的二次函数
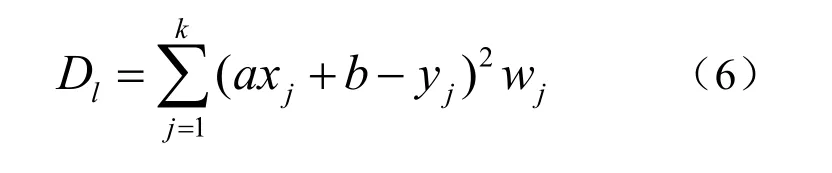

图9 延长端点后的重建曲线
3 实例与分析
作者在微机平台(P4 3.06G CPU,512M RAM)上用C++语言实现了本文提出的算法,下面给出应用该算法重建曲线的几个实例。图 10所示的是开点集的重建曲线(包括(a)波浪线和(b)螺旋线),可以看出重建曲线较好地反映了点集的形状,保持了尖点和端点的特征,有效避免了开曲线在点集端点处收缩退化的现象。图 1 1所示的是封闭点集的重建曲线,对于封闭点集,利用 BFS生成树去除旁支后得到的脊轮廓并非形成封闭的环(生成树的基本性质),但是由于脊轮廓的两个端点十分接近,甚至很可能是彼此邻接的,因此,可以根据其两个端点之间距离是否小于给定阈值来判断点集是否封闭,进而重建出所需的封闭曲线。图 1 2所示的是多连通点集的重建曲线,利用多连通点集的场分布也具有多连通性的特点,可实现对点集的区域划分,然后针对各个连通子集数据点的开闭特征重建出相应的曲线。以上实验表明,对于稠密且带噪声的平面散乱点集,本文算法可以有效重建出反映点集特征和形状的B样条曲线。

图10 开点集的重建曲线

图11 封闭点集的重建曲线

图12 多连通点集的重建曲线
表1分别给出了几个曲线重建实例的拟合误差和运行时间。其中,Error_Ave和Error_Max分别表示B样条重建曲线的平均误差和最大误差,其定义如式(7)所示

其中 di是各子集中数据点qi到对应的B样条重建曲线上参数点C)的投影距离。
对各种类型的点集,初始化生成数字图像的条件一致,即其分辨率都是根据点集分布密度进行自适应选择。对于本文提出的改进步骤,步骤1是用于提高效率的,步骤 2和步骤 3相比Goshtasby的算法会消耗一定的时间。从表1可以看出,步骤2和步骤3所消耗的时间大概占总重建时间的 15%~30%,时间消耗在可以接受的范围内,但曲线重建效果得到了显著改善。另外,值得注意的是,本文提出的曲线重建算法的主要目的是追踪散乱点集的脊线,所得到的拟合曲线也只是一次拟合的结果,并没有进行迭代计算以减小误差以及对曲线进行光顺处理。如果加上这些附加操作,则本文算法提出的两个步骤消耗的相对时间将会更少。

表1 本文各个重建实例拟合误差和运行时间的比较
4 总 结
本文在文献[1]算法的基础上,提出了一种更加实用的平面散乱点集的B样条曲线重建算法。相比文献[1]的算法,本文算法通过估计场强基函数的边界,提高了量子化生成数字图像的运算效率;通过引入图像细化以及 BFS生成树去除旁支,解决了冗余分支像素导致脊轮廓生成困难的问题;通过对开点集端点附近沿着脊轮廓延长线方向上的散乱点排序,改进了文献[1]在重建开曲线时端点处缩短的缺陷。如何将本文的重建方法推广到三维的情形,进而解决三维空间曲线的拟合问题,将是今后进一步研究的内容。
[1] Goshtasby A A. Grouping and parameterizing irregularly spaced points for curve fitting [J]. ACM Transaction on Graphics, 2000, 19(3): 185-203.
[2] Lee I K. Curve reconstruction from unorganized points [J]. Computer Aided Geometric Design, 2000, 17(2): 161-177.
[3] Pottmann H, Randrup T. Rotational and helical surface approximation for reverse engineering [J]. Computing, 1998, 60(4): 307-322.
[4] Hastie T, Stuetzle W. Principal curves [J]. Statistical Association, 1989, 84(13): 502-516.
[5] Lee E T Y. Choosing nodes in parametric curve interpolation [J]. Computer Aided Design, 1989, 21(6): 363-370.
[6] Hoschek J, Lasser D. Fundamentals of computer aided geometric design [M]. Wellesley, MA: A.K. Peters, 1993. 118-212.
[7] Farin G. Curves and surfaces for computer aided geometric design: a practical guide (5th edition) [M]. NewYork: Academic Press, 2002. 161-166.
[8] Levin D. The approximation power of moving least-squares [J]. Mathematics of Computation, 1998, 67(224): 1517-1531.
[9] Fang L, Gossard D C. Multidimensional curve fitting to unorganized data points by nonlinear minimization [J]. Computer Aided Design, 1995, 27(1): 48-58.
[10] Taubin G, Rondfard R. Implicit simplicial models for adaptive curve reconstruction [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(3): 321-325.
[11] Amenta N, Bern M, Eppstein D. The crust and the β-skeleton: combinatorial curve reconstruction [J]. Graphical Models and Image Processing, 1998, 60(2): 125-135.
[12] 钟 纲, 杨勋年, 汪国昭. 基于场表示的平面无序点集曲线重建算法[J]. 计算辅助设计与图形学学报, 2002, 14(11): 1074-1079.
[13] 钟 纲, 杨勋年, 汪国昭. 平面无序点集曲线重建的跟踪 算 法 [ J]. 软件学报, 2002, 13(11): 2188-2193.
[14] Lin H W, Chen W, Wang G J. Curve reconstruction based on an interval B-spline curve [J]. The Visual Computer, 2005, 21(6): 418-427.
[15] Hardy R L. Theory and applications of the multiquadrics-biharmonic method [J]. Applied Mathematics and Computation, 1990, 19(8/9): 163-208.
[16] Piegl L, Tiller W. The NURBS book (2nd ed.)[M]. New York: Springer-Verlag, 1997. 405-413.
[17] 柯映林. 反求工程CAD建模理论、方法和系统[M].北京: 机械工业出版社, 2005. 16-17.
[18] 吴宗敏. 径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 2002, 19(2): 1-12.
[19] Hilditch C J. Comparison of thinning algorithms on a parallel processor [J]. Image Vision Compute, 1983, 1(3): 115-132.
[20] Pavdis T A. Thinning algorithm for discrete binary image [J]. Computer Vision, Graphics and Image Processing, 1980, 13(2): 142-157.
[21] Rosenfeld A. A characterization of parallel thinning algorithms [J]. Information and Control, 1975, 29(3): 286-291.
[22] 张宏林. Visual C++数字图像模式识别技术及工程实践[M]. 北京: 人民邮电出版社, 2003. 235-251.
B-Spline Curve Reconstruction from Planar Unorganized Points Based on Field Distribution
HUANG Tong-xin1,3,4, WANG Wen-ke1,2,3,4, ZHANG Hui1,3,4, SONG Zheng-xuan1,3,4
( 1. School of Software, Tsinghua University, Beijing 100084, China; 2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China; 3. Key Laboratory for Information System Security, Ministry of Education, Beijing 100084, China; 4. Tsinghua National Laboratory for Information Science and Technology, Beijing 100084, China )
Curve reconstruction from planar unorganized points is one of the most important problems in reverse engineering. A practical B-spline curve fitting algorithm based on Goshtasby’s approach is presented. The digital image representing field distribution by estimating the bound of field strength basis function is generated at first, and then an algorithm of image thinning associated with improved BFS is proposed to overcome difficulties of obtaining the ridge contour under the situation of redundant branch pixels, and finally the weighted least squares method is used to extend the reconstructed curve for overcoming the deficiency that reconstructed curve may be shortened. Experiments show that the algorithm is valid and practical for B-spline curve reconstruction, especially when the given points are dense and noisy.
computer application; B-spline curve reconstruction; field distribution; unorganized points
TP 391
A
1003-0158(2010)02-0073-11
2008-08-16
国家“973”计划资助项目(2004CB719404);国家自然科学基金重点资助项目(60635020);国家“863”重点资助项目(2007AA040401)
黄童心(1984-),男,湖北咸宁人,硕士研究生,主要研究方向为计算机辅助几何设计。
