多管相贯线切割运动轨迹与位姿控制方法研究
2010-01-01曹建福张恒超
曹建福, 张恒超
(西安交通大学自动控制研究所,陕西 西安 710049)
随着各种建筑工程中钢网架结构的普遍应用,大量的钢管需要在数控管切割设备上进行相贯线切割作业。多管相贯线切割需解决相贯线轨迹计算以及割矩位姿的控制问题,关于这个问题已经有不少文章作过讨论[1-2]。本文在普遍采用的多管相贯数学模型基础上,采用一种新的处理方法对坡口切割运动进行控制,计算量相对现有的坡口控制方法大大降低,还可以明显改进管切割数控设备的性能。
1 多管相贯线数学描述
一般情况下相贯于一处的多管管件可以分为三类:主管、切管和交管,为了保证钢结构的稳定性,总是采取切细管的原则进行。以图1 中只有一根交管的三端头相贯为例,设定主管的外 壁半径为zR ,交管的外壁半径为jR ,切管的内外半径为nR 、wR ,切管轴线正向与主管轴线正向的夹角为qα ,交管轴线正向与主管轴线正向的夹角为 jα ,切管与交管轴线正向交角在主管横截面平面上的投影(称之为扭角)为β(如图2 所示),O-XYZ 坐标系原点O 与O′-X′Y′Z′坐标系的原点O′在Z′′轴方向上的距离(即管心交叉距离)为D。描述切管的坐标系O-XYZ 绕其Y 轴顺时针旋转qα 角度,就可以得到描述主管的坐标系O′′-X′′Y′′Z′′,而O′′-X′′Y′′Z′′坐标系先沿Z′′轴平移距离D,再绕其Z′′轴逆时针旋转β 角,最后绕新的Y′′轴逆时针旋转 jα 角度,就得到用于描述交管的坐标系O′-X′Y′Z′。

图1 三管相贯模型(沿Y′′向观察)
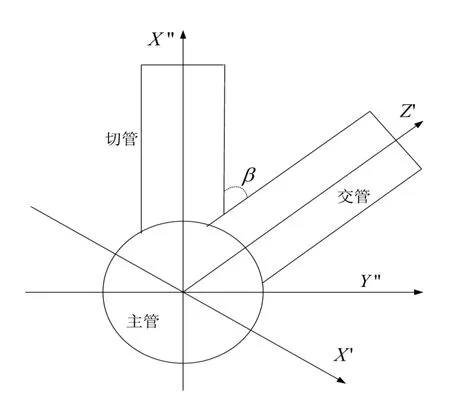
图2 三管相贯模型(沿Z′′向观察)
实际多管相贯线由切管与主管的相交线、切管与交管的相交线综合而成,采用“Z 最大值原则”,即在切管坐标系内根据切管的XY 坐标,求得切管圆周内各点处与主管的相交线和与所有交管的相交线,然后取相同XY 值在相贯线上Z 值最大的那个点,由所有这些最大Z 值点拟合出封闭曲线就是实际的相贯线。若交管大于一根,则其余交管可做相同计算处理。描述切管与交管的空间位置关系均以主管为参考,这样可以用统一的数据格式表示各个管件与切管的相对位置,既避免了对任意两个空间管件进行角度变换计算,又方便在实际控制系统应用中进行参数输入操作。
经过推导,切管与主管以及切管与各个交管相贯线的参数方程为

其中 Rji和 Rz分别为交管和主管的外半径,zji为切管与第I 根交管的交线。
公式(1)iD 为第i 根交管与切管在主管轴心上交点的偏心距,αji(i ≥ 1)为第i 根交管轴线与主管轴线的交角,βi为第i 根交管轴线相对于切管和主管轴线构成平面的扭角。其中
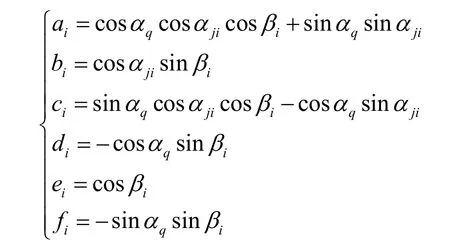
实际割矩轨迹的方程为

这里max( zji)是对同一(x, y)点由各个交管求得zji的最大值。
切割时需将圆周进行离散化,将计算得到的离散点坐标赋予控制系统,就可以得到离散的切割相贯线。假设对切管圆周按N 份均匀离散,则 离散步长为(360/ )N °,此时离散化的x 和y 为
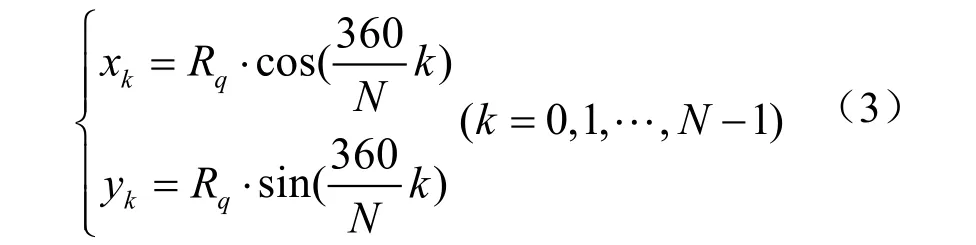
将式(3)的离散kx 和ky 代入式(2)并结合式(1),就 可以得到各个离散点处的z 值kz 。
2 多管相贯线切割运动轨迹与割矩姿态控制算法
2.1 割矩姿态角的一般数学模型
由相贯线方程可求得切割点处法剖面垂直 于相贯线平面的两面角Ψ 。根据两面角Ψ ,按照API 标准,求出坡口角φ
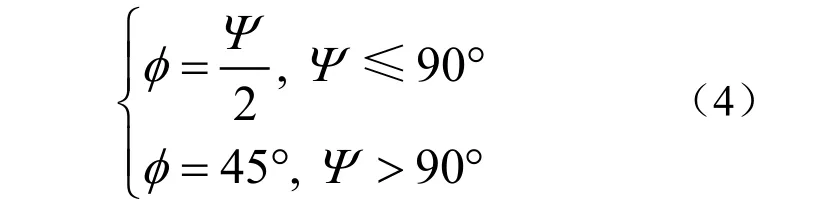
根据两面角Ψ 和坡口角φ,求理论切割角ρ

两面角、坡口角和理论切割角均定义在法剖面内,而实际切割时割矩只能在切管上某一切割点处的支轴剖面内摆动(见图3)。而实际位于支轴剖面内的割矩姿态角ω 很难精确获得,一般由以下经验公式得到

式(6)中γ 为法剖面与支轴剖面之间的夹角。
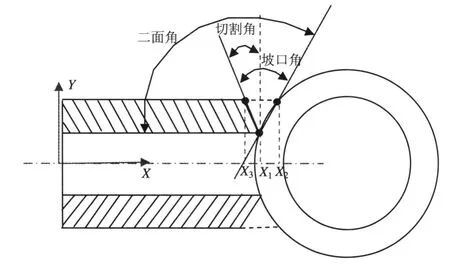
图3 管相贯坡口示意图
这种割矩姿态角的计算方法,有两点缺点:① 要处理的空间几何关系很多,而且最终的割矩姿态角是由经验公式得到的;② 仅适用于相贯线具有统一数学表达式的情况,对于多管相贯的情况,由于相贯线是若干表达式的组合,并没有统一的表达式,所以采用这种方法编制程序的工作量会相应增大很多。
2.2 割矩姿态角的简化数学模型
由上面的讨论可以知道,实际切割系统的割矩只能在支轴剖面内摆动,如果可以直接近似得到支轴剖面内的切割角,而不是借助其它间接的空间角度计算得到,计算量将会大大降低。
对于式(2)中的每一个参数角度θ,切管与主管的相贯形状如图4 所示。
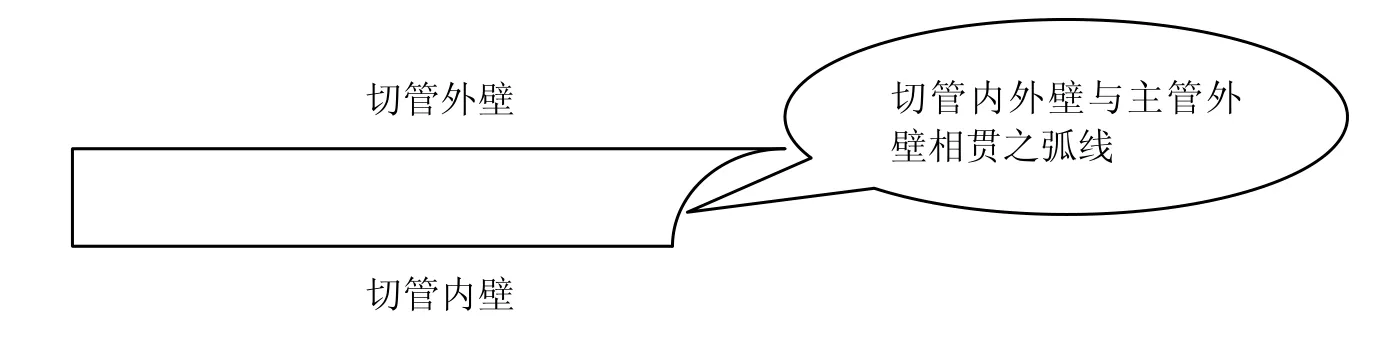
图4 切管内外壁相贯端面示意图
一般切管壁厚较之切管横截面直径小很多,故可以用空间直线近似取代切管内外壁与主管外壁相贯之弧线进行支轴剖面内坡口角度的计算,如图5 所示。
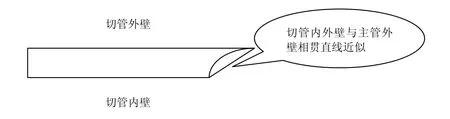
图5 切管内外壁相贯端面近似示意图
在相贯线的计算公式中,分别代入切管的内半径qnR 和外半径qwR ,从而可以求得多管相贯的两条相贯线,分别为切管内壁相贯线qnz 和切管外壁相贯线qwz 。假定用户设定的焊接坡口角度为η,则实际割矩姿态角度大小为
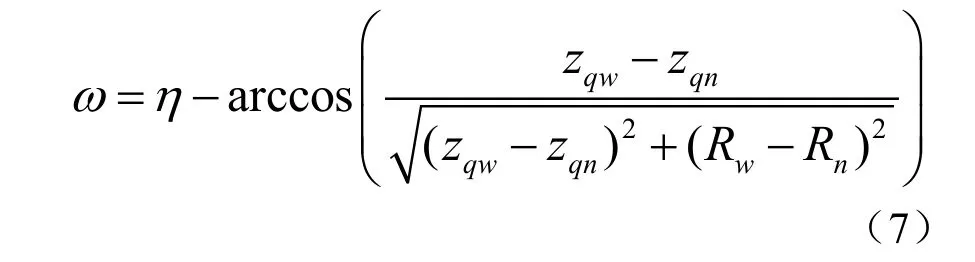
实际切割时,割矩是在切管表面切割的,由于坡口角的存在,割矩实际切割点会偏离理论值,所以在切管表面沿轴线方向要进行纵向补偿,补偿量Δ 为
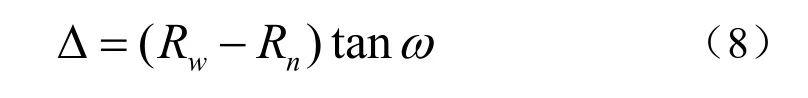
在式(7)和式(8)中,利用离散化qnz 和qwz 数据,结合式(2)和式(3)可求得在离散角度k处的kω 和kΔ 。
2.3 多轴联动运动控制代码生成算法
根据以上公式,可求得离散位置值kz 、kω 。对于相贯线端头切割,W 轴每次旋转度,X轴运行kz +kΔ ,同时B 轴摆动kω 。多轴联动控制代码生成算法如下:
(1) 设离散步长 1θΔ = °,利用公式(2)对z 进行离散化处理,即得[ ]z i (i=0,1,…,359)表示离散参考角度θ =处的z 值;
(2) 根据式(7),计算各个离散[ ]z i 处的坡口角度 [ ]iω (i=0,1,…,359);
(3) 根据式(8),计算 [ ]z i 的补偿量Δ[ i ](i=0,1,…,359)。
在所获得的各离散处W 轴、X 轴和B 轴坐标值基础上,相邻离散点之间相贯线轨迹采用小线段逼近方法,即生成多轴联动运动的控制代码。多轴联动直线插补可采用粗精两级DDA 算法。
3 实际切割实验及结果分析
利用本文提出的方法开发的6 轴管切割控制系统,已用在某企业的数控管切割机上。在该数控管切割机上对管件材料实际进行切割,进行了两部分的数据测试,即无坡口的管件切割和有坡口的管件切割,下面分别对这两种情况的各类端头进行数据分析。
3.1 无坡口管件的加工数据分析
实际加工时,选取了直交端头、斜交端头、斜截断端头、偏心斜交端头、双重相交端头、双斜截断端头以及支管两端头的数据进行分析。在给出各种端头相关参数的情况下,通过对理论值和测量值进行比较,计算出了各种端头误差的绝对值。
(1) 直交端头
切管外直径为 110mm,交管外直径为160mm,切管壁厚为2.5mm,表1 为相应坐标处的理论值和实际切割后测量值,同时计算出了绝对误差。
通过表1 可以看到,各测量点处平均误差绝对值为0.6mm,最大误差绝对值为0.9mm,符合设计技术指标。
(2) 斜交端头
切管外直径为 110mm,交管外直径为160mm,切管壁厚为2.5mm,相贯斜交角度为60°。表2 为相应参考坐标处的理论值和实际测量值,同时计算出了绝对误差。

表1 直交端头数据

表2 斜交端头数据
通过表2 可以看到,各测量点处最大误差为0.9mm,平均误差绝对值为0.5mm,符合设计技术指标。
3.2 有坡口管件的加工数据分析
共有3 种坡口形式,即定角坡口、定点坡口和固定坡口。有代表性地选取了斜交端头、偏心斜交端头和双重相交端头的数据进行分析。通过对理论值和测量值进行比较,计算出了各种端头的绝对误差。
(1) 斜交端头
实际切割时,切管外直径为110mm,交管外直径为160mm,切管壁厚为2.5mm,相贯斜交角度为60°,坡口为30°定角坡口。表3 为相应参考坐标处的理论值和实际测量值,同时计算出了绝对误差。
通过表3 可以看到,各测量点处最大误差为0.8mm,平均误差绝对值为0.4mm,满足技术设计指标。
(2) 偏心斜交端头
实际切割时,切管外直径为110mm,交管外直径为160mm,切管壁厚为2.5mm,相贯斜交角度为60°,相贯偏心距离为20mm,坡口为30°固定坡口。表4 为相应参考坐标处的理论值和实际测量值,同时计算出了绝对误差。

表3 斜交端头(定角坡口)

表4 偏心斜交端头(固定坡口)
通过表4 可以看到,各测量点处最大误差为0.8mm,平均误差绝对值为0.4mm,满足设计技术指标。
4 结 论
对具有复杂坡口的多管相贯线切割问题,现有的运动轨迹与姿态控制方法计算量较大,严重地影响管切割控制系统的性能。不同于现有坡口切割方法,本文根据内外相贯线在切管轴剖面内近似实际切割坡口角的思想,提出了一种新的割矩位姿控制算法。利用本文的方法开发了6 轴管切割机控制系统,通过实际切割表明该控制系统对坡口控制精度较高,可明显提高多管相贯线的切割效率。
[1] 季 忠, 刘 韧. 管管相交数学模型及其在数控加工中的应用[J]. 工程图学学报, 2002, 23(2): 139-144.
[2] 甄洪栋, 季 忠, 刘 韧, 等. 多管相贯数学模型及其在自动切割中的应用[J]. 山东机械, 2004, (6): 23-26.
[3] 李宝清, 贾东安. 多管板相贯坡口切割数学模型[J].天津大学学报, 2000, 33(5): 583-586.
[4] 王国栋, 阎祥安, 肖聚亮, 等. 管端相贯线坡口切割割矩位姿控制[J]. 天津大学学报, 2005, 38(8): 684-688.
[5] Liu Tan, Yu Tao, Wang Wenbin, et al. Mechatronics and automation [C]//IEEE International Conference, 2005: 1750-1755.
